
- 脳神経系に興味がある人
- 生体信号の数学的モデリングに興味がある人
- Hodgkin-Huxley(ホジキンハクスレー)モデルについて詳しく知りたい人
こんにちは.
脳神経系の事柄を取り扱う工学寄りな本には,必ずと言っていいほど出て来る方程式があります.
それは,
Hodgkin – Huxley モデル
脳神経細胞の活動を模したモデルで1952年に論文で発表されました.
ちなみにこちらが原著論文になります.
己の理解を再確認するためにHodgkin-Huxley モデルについてスライドも作りました.

ホジキンさん,ハクスレーさんが作ったモデル式は,65年経った今でも脳神経系の分野で非常に有効で使っている人はたくさんいます.
脳を研究している研究者はすでに知っているかもしれまでんが,これから脳分野の研究をしたい!と志す方はぜひ,理解を深めてください!
ニューロンの活動電位について
少し,ニューロンの活動電位についておさらいしておきましょう.
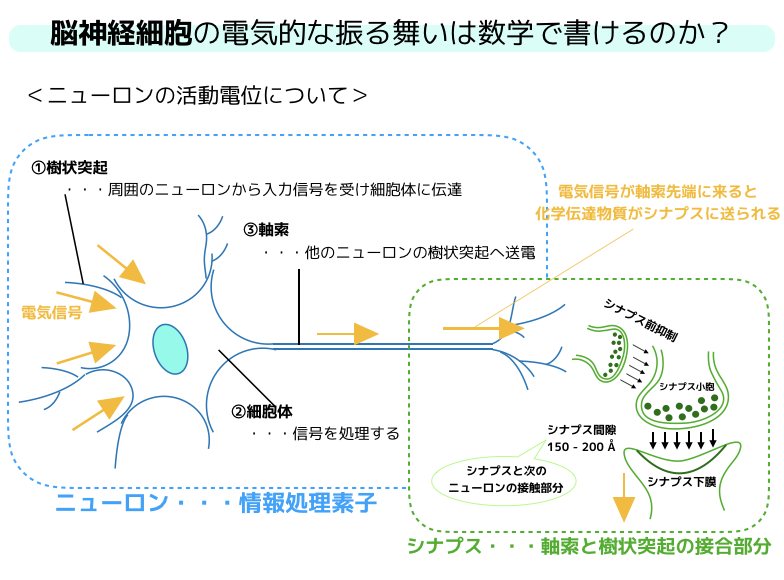
ニューロンは中心部に信号を処理する細胞体があって,周りに多数の短い樹状突起と長く伸びている軸索によって構成される単一の細胞です.
樹状突起は,ニューロンの受容経路であり,軸索は伝送回路の役割を持っています.
上の絵からも確認できると思いますが,どのニューロンも軸索の先には他のニューロンの樹状突起があり,情報伝達リンクを作っています!
また脳内のニューロンの数は膨大で,例えばヒトの脳のビー玉ほどの大きさの領域には三億個程度,ニューロンが含まれているのですが,
これはアメリカの人口(3.3億人)とほとんど同じくらいですね.
ビー玉1個にアメリカの人口と同じくらいの数,,,膨大です.
(脳全体では,200億ものニューロンが存在すると言われています.)
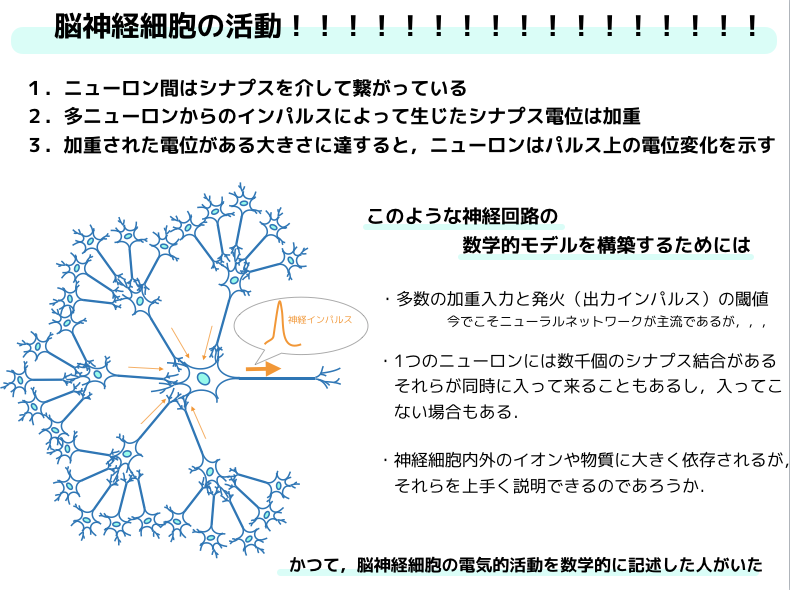
今でこそ,こう言った脳神経系を模したニューラルネットワーク(モジュールの集合を扱える)が騒がれていますが,当時はインターネットやビッグデータという概念もなく,GPUなんて,,,,って話ですからね.
こんな時代に,脳神経活動のモデリングをするなんて無理ゲーだ!なんて思う方もいらっしゃるかもしれません.
しかし,ヒトの脳のニューロンの数と情報経路の数はかなり膨大で複雑ですが,普通の細胞でできた物質の塊にすぎないし,それを化学的かつ電気的な原理で作動すると考えてモデリングをするということは出来たようですね!
しかし,,,ホジキンさん,ハクスレーさん天才だ.
彼らが書いた論文のおかげで,複雑な脳活動の基本的な機構,つまり物理法則や生物学の観点からきちんと機能を考えることができるというきっかけを与えるモデルになると思います.
ヤリイカを使った!?
ちょっとここでヤリイカを取り上げます!
なぜかというと実は,数学的なモデルのパラメータを色々と決めるときに,ヤリイカの巨大軸索を用いて数学モデルの構築をしました.
しばしば実験に使用されるヤリイカですが,ヤリイカの巨大軸索は直径が 0.4mm から 0.7mm程度もあって実験し易いのですね.
実験がし易いというのは,電位固定法と呼ばれる方法で実験ができるからです.
電位固定法とは,軸索の内側に直接電極を刺して,軸索の内側と外側の電位差を操作できるものです.
(ヤリイカから発生する活動電位とは別に,人工的な特定の電位を流すことができる)
余談ですが,0.4mm ~ 0.7mm程度もあるこの軸索,ヤリイカが海水をジェット噴射して泳ぐ際に,神経インパルスを体の隅々に高速に伝達するためにあります.
(そんなことはどうでもいいですね笑)
軸索でのインパルスの発生について,スライドに入らなかった分の加筆をします.
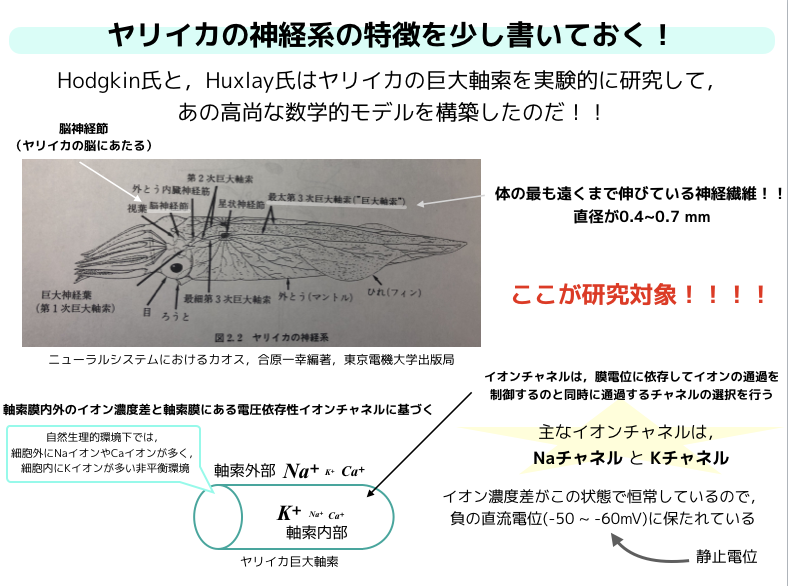
軸索でのインパルスの発生は,軸索膜内外のイオン濃度差と軸索膜に存在する電圧依存性のイオンチャネルによって起こります.
ヤリイカの軸索の周りを例えば海水で浸した場合,主要なイオン組成はスライドのようになります.
つまり,自然下において,細胞内に\(K^+\)イオンが多く,細胞外は\(Na^+\)や\(Ca^+\)が多い非平衡な状態です.
通常の環境下の軸索膜では主に\(K\)チャネルのみが開いていて,K+に対する透過性が良いです.
さらに軸索膜の内外でイオン濃度差が恒常的に保たれているので,軸索内の電位は軸索外の外液を基準にして負の定常直流電位になっています.
この時の膜電位を静止電位と言います.
(参考:ニューラルシステムにおけるカオス,合原一幸編著,東京電機大学出版局)
静止電位では,軸索は安定な状態です.
しかし,加わる電流パルスがある値を超えると,膜電位の応答が劇的に変化します.
大体はこのような感じです!
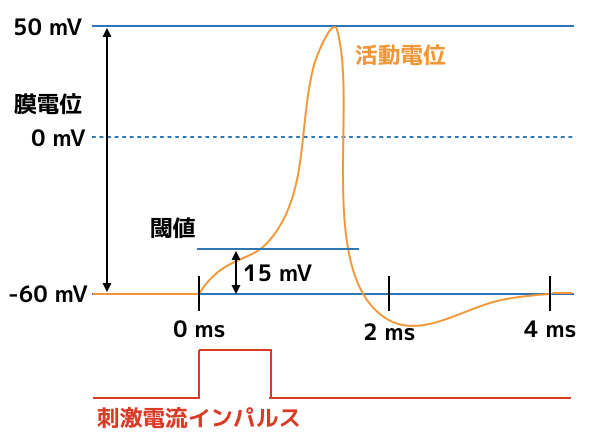
刺激インパルスが入り,膜電位がある値(おそよ15mV)を超えると,静止電位から一気に110mV程度の電圧まで到達します.
この電位変化を神経インパルスと言います.
Hodgkin-huxleyモデル
では,実際のHodgkin-Huxleyモデルについてと,実際の挙動(膜電位)について原著論文から引っ張ってきます.
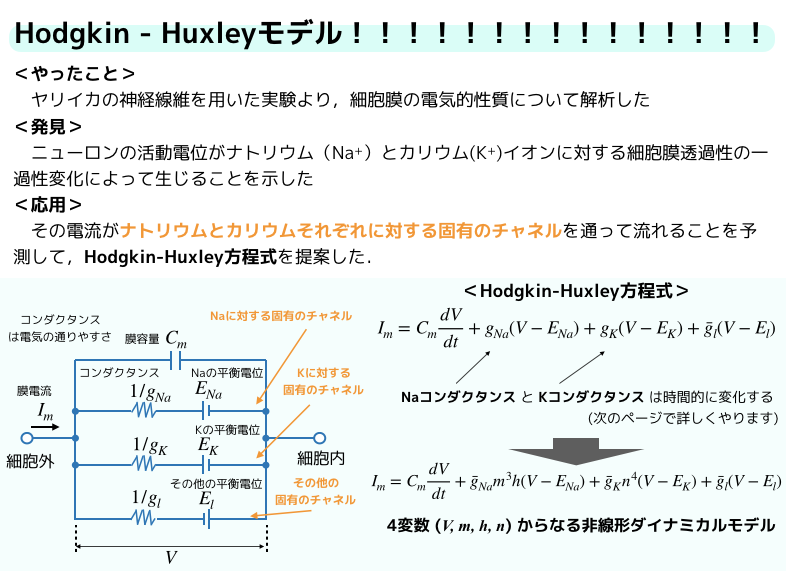
こちらにも,スライドに入りきれなかった説明を追加しておきます.
Hodgkin-Huxleyモデルは,神経興奮の電気的現象をモデル化したものです.
それを4つの非線形の連立微分方程式にまとめました.
上のスライドのその他の平衡電位\(E_I\)は,リーク電流です.
(ほのほとんどがClイオン)
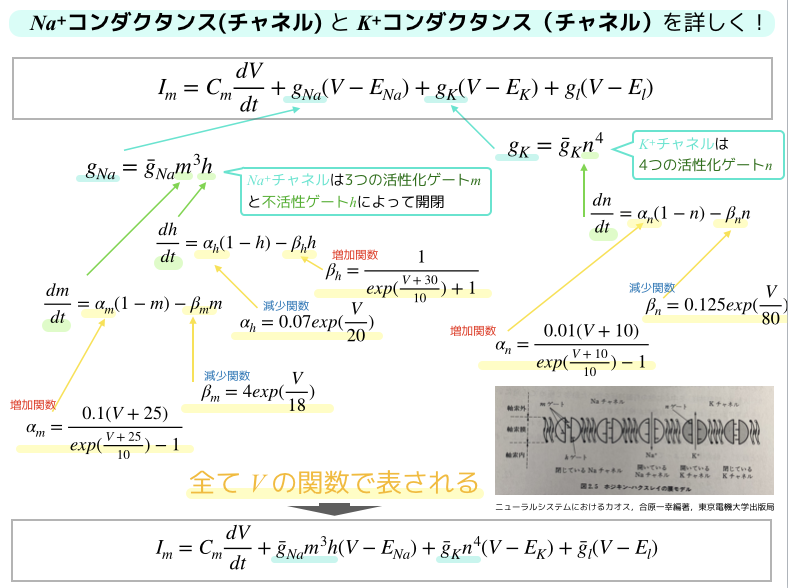
このとき,ナトリウム\(Na^+\)チャネルは3次のべき乗の活性化変数\(m\)と不活性化変数\(h\)で構成されており,\(K^+\)チャネル(カリウム)は4次のべき乗の活性化変数\(m\)でモデル化されています.
これらのべき乗の項のモデル化の役割は,電位固定法で得られたイオン透過度を説明するためのものでした.
驚くべきことに,1998年になんと.イオンチャネルの分子的構造が解明されるわけですが,ホジキンハクスレーモデルの活性化変数と不活性変数の冪の個数と,分子的構造から解明された活性化ゲートと不活性化ゲートの個数が一致していることが分かりました.
(論文はこちら:The structure of the potassium channel: molecular basis of K+ conduction and selectivity.)
また,各\(\alpha\)と\(\beta\)は,膜電圧Vに依存した値ですが,これはヤリイカ巨大軸索の実験データと比較して,最もフィッティングした場合を参考に作っています.
実際に,この4つの方程式を解くと,以下のような結果が得られます.
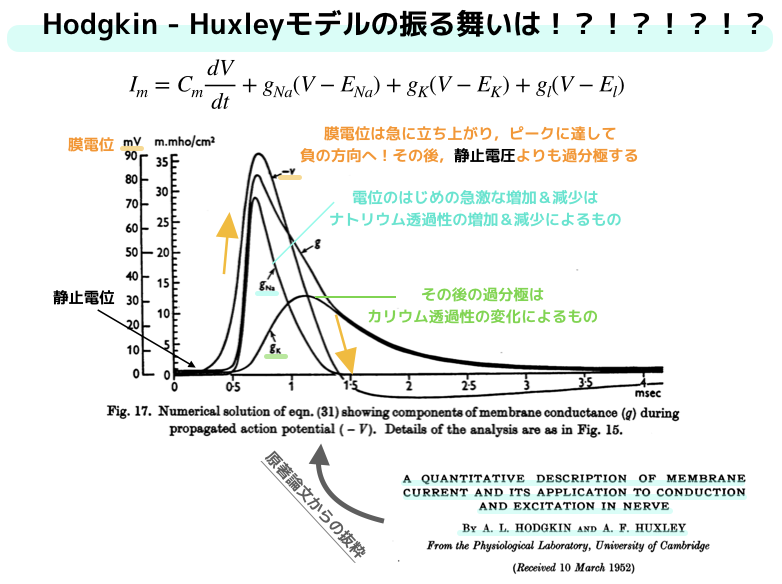
方程式から定まる活動電位の振る舞いと,実際のヤリイカの活動電位の振る舞いはかなりの一致が見られており,
さらに電気的興奮膜のミクロな存在形式の概念を明確に示しています.
また,こういった実験的アプローチと理論的アプローチの重要性を詳しく理解したい方は,「計算論的神経科学」という本が非常におすすめです.

計算論的神経科学は,2019年6月に出版された最新の本だよ!面白いよ!
以下の4つは,「ニューラルシステムにおけるカオス,合原一幸編著,東京電機大学出版局」からの抜粋ですがこのような事をHodgkin-huxleyモデルは示しています.
- 刺激受容部は電圧感作する(膜に電圧リセプタがある)
- 特定のイオンのみを透過させるようなイオン選択的膜チャネルが離散的に存在する
(\(Na^+\)チャネル,\(K^+\)チャネル,リーク(\(Cl\))チャネル)- チャネルには開状態と閉状態がある.
- ヤリイカ巨大軸索には3つの独立したゲート(m,h,n)がある.
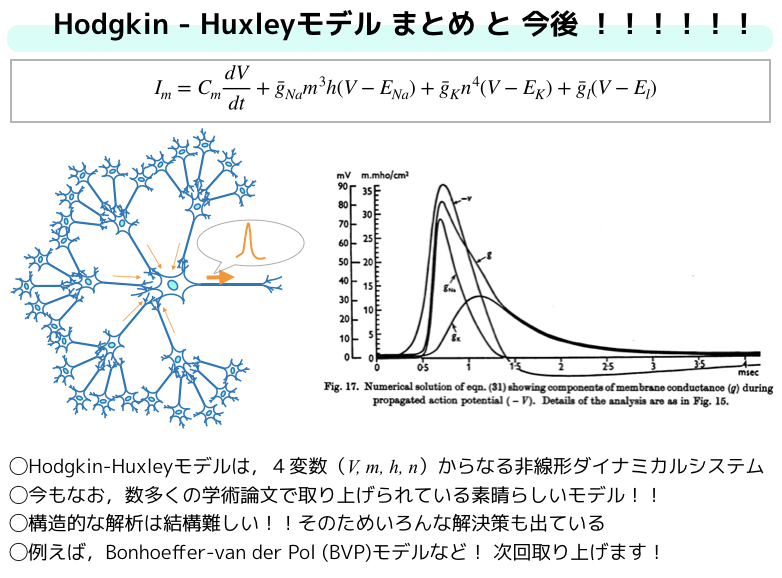
すごいですね!
Hodgkin-Huxleyモデルは4変数からなる非線形ダイナミカルシステムですが,実は現在ではその本質を残したまま2変数で解けるBVP (Bonhoeffer-van der Pol) モデルというものもあります.
次回は,実際にシミュレーションをしたり,BVPモデルを扱っていきます!
では〜!






いきなり申し訳ございません。
Hodgkin-Huxleyモデルを理解するには、どの本が一番おすすめですか?