
- 数学が好きな人
- 弧度法で何ができるのか知りたい人
- 受験生やその他高校生.
こんにちは.
今日は弧度法について,なるべく分かりやすく,書いていきたいと思います.

全然難しくないから安心して!!
弧度法とは何かというと,「円弧の長さから角度を求める方法」です.
これ,すごくないですか!?
円の弧の長さが分かれば,角度が求まるのですよ!
凄いやつだから,最後まで覗いて見てください!
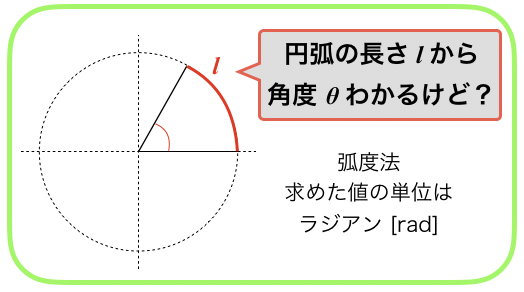
この方法で角度を求める方法を「弧度法」といいます.
また,この方法によって定まった角度の単位を「ラジアン」といいます.
「rad」と書きます.

ちなみに,日頃僕たちが角度を求めるときに,使っているのは度数法というぞ!度数法は,円を360等分したものを1度というものしているんだね!
動画解説も出しました!
弧度法を求める
弧度法の単位はラジアンといいました.
では,1ラジアン (1 rad)を考えていきましょう!
(度数法の1度は,円を360等分したものの1つでしたね!)
実はめちゃくちゃ簡単です!
単位円の円弧の長さが,そのまま弧度法で言うところの角度(厳密には弧度といいます)になるので,
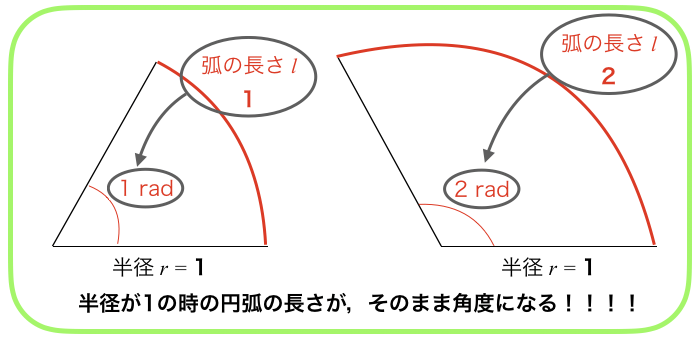
- 単位円の円弧の長さが1のとき, 1 rad
- 単位円の円弧の長さが2のとき,2 rad
です.
単位なんで,半径は1です.

えっ!?こんな簡単なんだ!!
度数法と弧度法の対応!
この絵で瞬殺です.
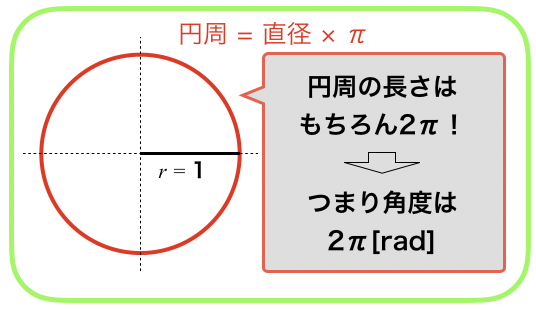
弧度法だと,半径1の単位円の円弧が直接角度[rad]になります.
よって,円の角度は何ラジアンかというと,円周の長さになるので,2π [rad]になります.
度数法だと,円を360等分しているので,度数法と弧度法の関係は,
360° = 2π [rad]
になります.
2で割ると
180° = π [rad]
ですね.
なんで弧度法が必要か!?
弧度法というものがなぜ必要なのか,それは人々は楽をしたいからなのです.

エレベータ万歳!!
学校から帰るときは,歩くより,車で帰りたいのが人間ですし,さらに近道もしたい!っていうのが人間です.
家に帰るという目的をいち早く達成するために,いろんな道具や最適ルートを探すのですね.
数学も一緒です.
実は,弧度法があると,扇型の円弧の長さlや面積Sが楽に計算できちゃうのです.
扇型の円弧の長さl
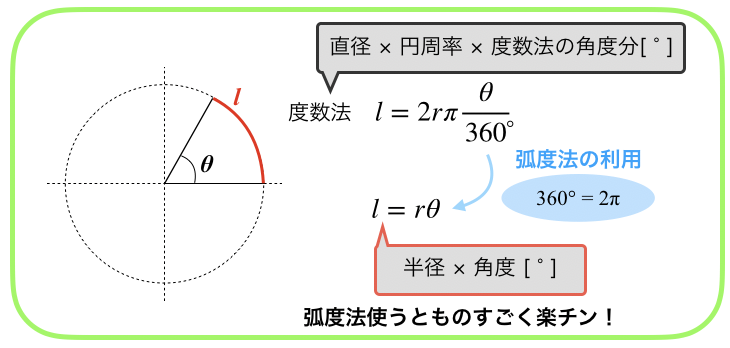
おうぎ形の面積S
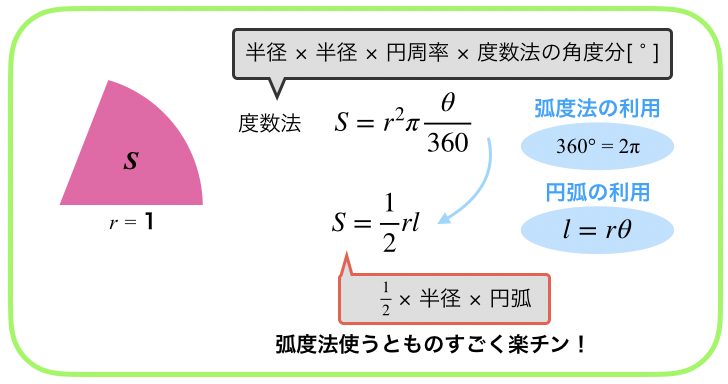
超簡単になりましたね!
2018年センター試験2Bの問題で一番はじめに出た
第1問で速攻こんな問題が出ました.
(1)1ラジアンとは,[ア]のことである.[ア]に当てはまるものを,次の⓪〜③のうちから一つ選べ.
⓪ 半径が1,面積が1のおうぎ形の中心角の大きさ
① 半径がπ,面積が1のおうぎ形の中心角の大きさ
② 半径が1,弧の長さが1のおうぎ形の中心角の大きさ
③ 半径がπ,弧の長さが1のおうぎ形の中心角の大きさ
がでましたが,きちんと理解していたら,すぐに[ア]は②だと分かりますね!

しっかりおさえておこうね!
では〜
こちらの記事もオススメです!
「二項定理ってなんだよ!多項定理ってなんだよ!!ってなっている君へ」
この記事はこんな人にオススメです 二項定理や多項定理をしっかり理解したい人 数学が好きな人 理系大学生や現役高…







弧度法を用いる最大のモチベーションはsin xの微分計算にあるかと思います.度数法で
lim_(x→0)sin x°/x=π/180となるのでこのことからsinx°をxで微分すると(π/180)cos x°となりsinやcosを微分するごとにその回数分のπ/180がかかってくるため計算が煩雑になります.これを避けるための一つの手段として弧度法による単位変換をしているかと思います.