サポートベクターマシンの詳しい理論的な解説について【線形分離可能な場合】

この記事はこんな人におすすめです．

サポートベクターマシンの理屈を詳しく理解したい人
機械学習の勉強をしている人
人工知能の勉強をしている人

こんにちは．けんゆー（@kenyu0501_)です．
ここでは，サポートベクターマシンの理論的な解説をしていきます．
色々と長くなってしまそうなので，とりあえず線形分離可能な場合のみでまとめます．

サポートベクターマシンSVM

マージン最大化する線を引くこと

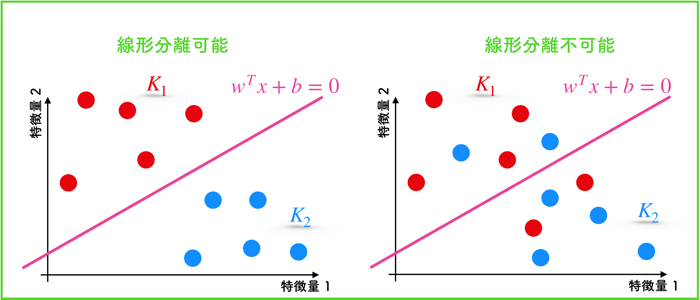
２つのクラスK1とK2をもつ，線形分離可能なデータに対して，マージン最大化する線を引くための理論的な解説を行います．

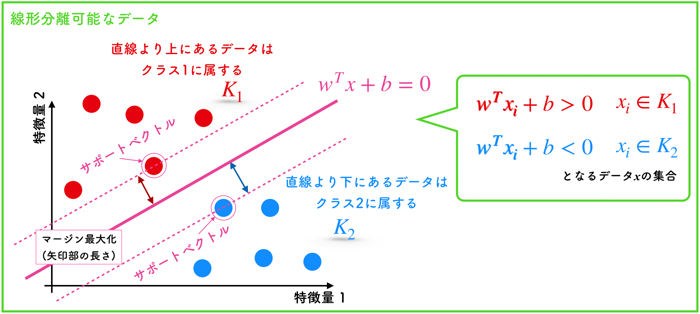
サポートベクターマシンは，上の図のような線を引くことです．
直線よりも上にあるデータは，クラス1(K1)に属し，直線よりも下にあるデータ群はクラス2(K2)に属します．
SVMでは，n次元実数ベクトルwと，バイアスと呼ばれるスカラー変数bをマージン最大化するような最適化問題を解くことによって決定します．(2次元空間だと，それぞれ，w：傾き，b：切片に対応するものです．)

ハードマージン

線形分離が可能な場合，訓練データの点全てを正しく分類できるような，パラメータwとbの組が存在しているという仮定のもとSVMを用います．
最適化問題を解くときに，線形分離可能を仮定した場合の標準的な定式化を行います．
このような線形分離可能性を仮定したSVMによる分類をハードマージンと呼びます．
以下では，ハードマージンについての定式化を行なっていきます．

2つのクラスの条件を扱うために

ここで，2つのクラスの条件を扱いやすくするために，ラベル変数tを用意します．

ラベル変数t

i番目のデータがK1に属する → t=1
i番目のデータがK2に属する → t=-1

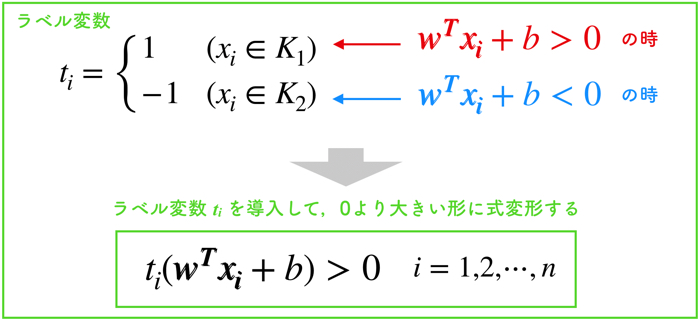
ラベル変数tを用いて，全てのデータに対して式が0より大きいという条件を満たすような形にします．
この条件を満たしながらマージン最大化をします．

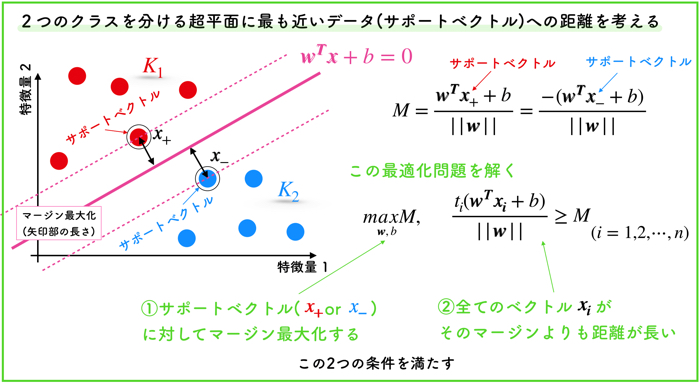
点と超平面(直線)の距離について考える

ここで，単純な点と超平面の距離について考えます．
マージン最大化をするものは，この点と超平面の距離だからです．
まずは高校数学の復習として，「2次元平面上の点と直線」について考えた後で，「n次元空間の点と超平面の距離」に拡張した方が考えやすいかもしれないです．

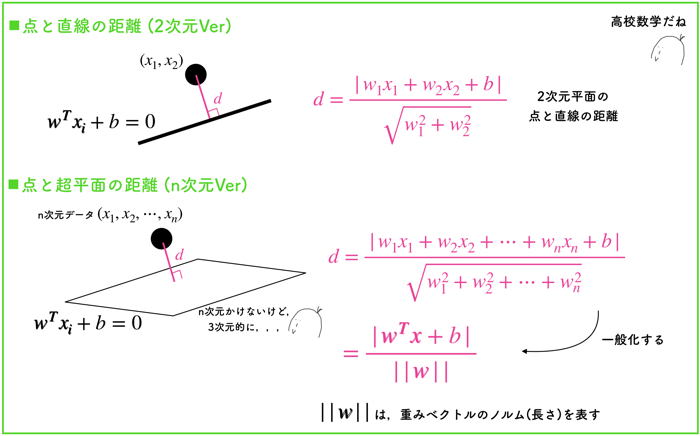
ここで，||W||はノルムと言われるもので，簡単にいうと単純な長さのことです．

マージン最大化をするための最適化問題

以上の要素を踏まえて，マージン最大化を以下の最適化問題に置き換えます．
ここで，マージンをMという記号で置き換えています．

一般的にこの最適化問題を解くためには，以下2つの条件を満たす必要があります．

2つのクラスを分ける超平面に最も近いデータ（サポートベクトル）への距離(マージン)を最大化すること
そのマージンに対して，他の全てのベクトルと超平面の距離が離れていること

最適化問題の式変形

マージン最大化を最適化問題へと定式化し，置き換えることができましたが，より計算をしやすいような変形をしておきます．

手順

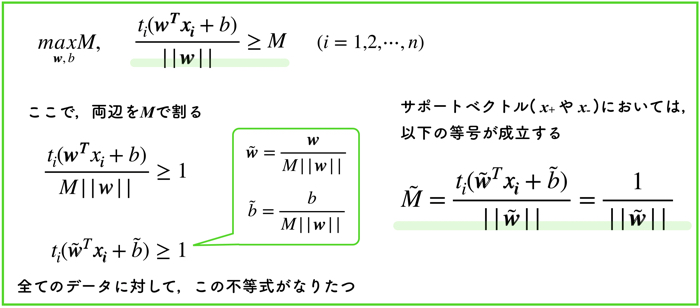
導出した最適化問題をマージンMで割る
w~とb~を導入して式をシンプルにする．
サポートベクトルのおいては，M~が成り立つ(2より)．
M~が超簡単になる

最大化問題を最小化問題に置き換える

ここでは，さらに計算の都合を良くするために，最大化問題を最小化問題にしましょう．
最適化問題を解くときには，最大化するよりも最小化にするようが解を探しやすいのです．
そのために，よく逆数の最小化を求める，という作業をして，最大化問題を最小化問題に置き換えることがあります．

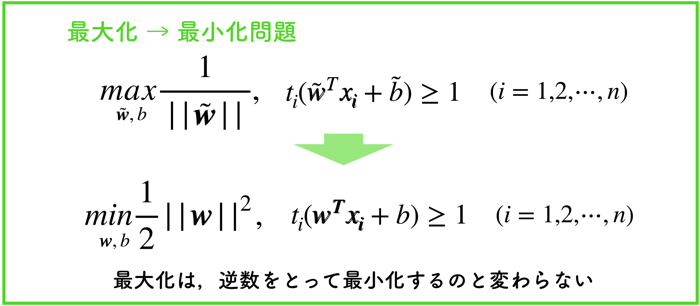
最小化問題の，2分の1や，2乗というのは，のちの最適化計算をやりやすいようにしているだけなので，あまり気にしないでください．
以上の最適化問題による定式化をハードマージンと呼ぶのでしたね！

ちょっとした特徴

このような最適化計算を行って，マージン最大化というものを行います．
今回行ったハードマージンのマージンの幅に関しては，サポートベクトルのみによって定まってしまいます．
そのため，サポートベクトル以外を取り除いても，分離境界は変化しません．

実際の計算はソフトマージン！？

しかし，実際にSVMで平面を引くときにも，まだ直接これを解くわけではありません．
なぜなら，ハードマージンでは，訓練データを完璧に分類できる関数(wx+b)が存在するという仮定をおきましたが，これは仮定が強すぎます．実際のデータはより複雑で，線形分離可能ではないデータの方が多いはずです．
（完璧に線形分離ができるという確証があればハードマージンでも構わない）

そのため，この後にもう少し特殊な変形がありますが，大体SVMの数学的な理屈は大体同じです，
SVMの最適化問題を解くときに，制約条件をちょっと弱めてあげるという方法をとります．