【フーリエ解析02】複素フーリエ級数とは？フーリエ級数が理解できていれば簡単！【解説動画付き】

こんにちは．けんゆー（@kenyu0501_)です．
前回のフーリエ級数に引き続き，今回は「複素フーリエ級数」の説明をしていきます．

（フーリエ級数自体を理解していない方はこちら）
フーリエ変換を理解する上でも，複素フーリエ級数の理解は必須です．

しかし，\(\cos\)や\(\sin\)で展開するフーリエ級数が理解できている人はとても簡単な内容だと思います．
まずは，これまでやってきた「フーリエ級数」との違いをざっくりと確認して「複素フーリエ級数」に関しての理解を深めていきましょう！

「フーリエ級数」と「複素フーリエ級数」のイメージの違い

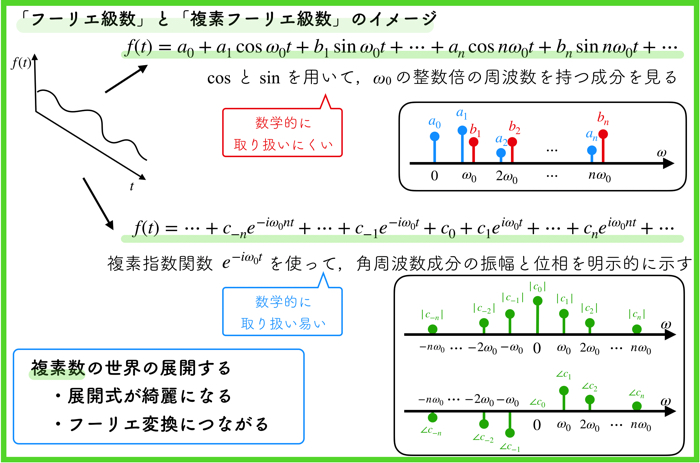
「複素フーリエ級数展開」の理論を理解する前に，「フーリエ級数」との違いを確認してください．
あらゆる関数は，フーリエ級数で展開できることは，前回やりました．
\(\cos\)や\(\sin\)を使った実数の世界の展開です．
実は，三角関数のみを使った展開は，数学的に取り扱いにくいのです．
周波数成分の振幅や位相というものを導出する際に，色々と式変形を伴うのです．

しかし，複素フーリエ級数は，それら周波数成分の振幅や位相が，フーリエ係数のみで明示的に表されるので，分かり易くなります．

「複素フーリエ級数」は三角関数の\(\cos\)と\(\sin\)の展開ではなく，複素指数関数\(e\)を使った展開になります．
ただそれだけです．
しかし，複素指数関数\(e\)自体も，三角関数の\(\cos\)と\(\sin\)から構成されているので，性質自体はほとんど一緒です．
複素指数関数\(e\)で展開するメリットは以下です．

• 展開式が綺麗にまとまる
• フーリエ変換につながる
• 周波数成分の振幅と位相が明示的に表現される

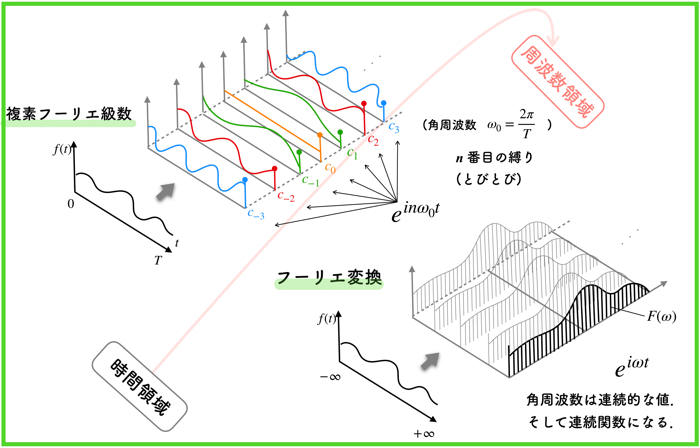
複素フーリエ変換に関しては，有限な積分区間\(T\)があります．
ここは，フーリエ級数の概念と同じです．
有限な区間Tの周期関数になりましたね！

しかし，フーリエ変換の場合は，この区間が\(-\infty\)から\(\infty\)までになりますが，またこの話は後日．．．
(フーリエ変換の内容を知りたい方はこちら「フーリエ変換って何？？」)

複素指数関数\(e\)はどういう波になるの！？【イメージ】

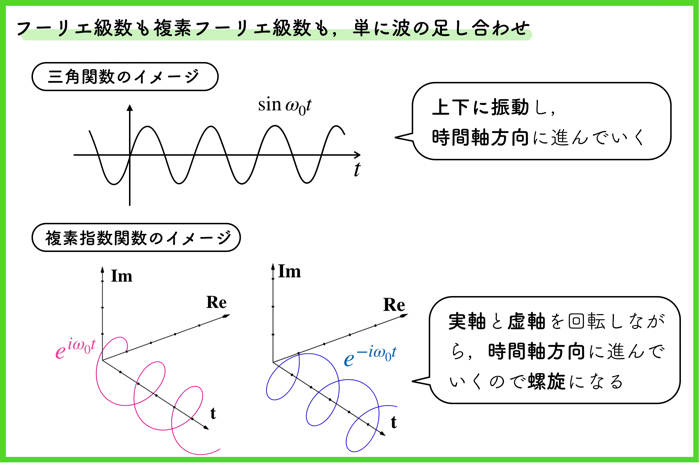
三角関数である\(\cos\)と\(\sin\)は，時間的に上下に振動する波でした．
一方で，複素指数関数\(e\)は，「螺旋」のような波をイメージすると分かりやすいと思います．
ここら辺の理解は「道具としてのフーリエ解析」を参考にしました．

複素指数関数\(e\)は，複素数なので実軸Reと虚軸Imがあります．
角周波数\(\omega_0\)で実軸と虚軸をぐるぐる回転しながら，時間方向に進むような波ですね．
\(e^{i\omega_0t}\)であれば，反時計回り(上の図のピンクの螺旋)になります．
\(e^{-i\omega_0t}\)であれば，時計回り(青の螺旋)になります．

オイラーの公式を使用して複素フーリエ級数への拡張

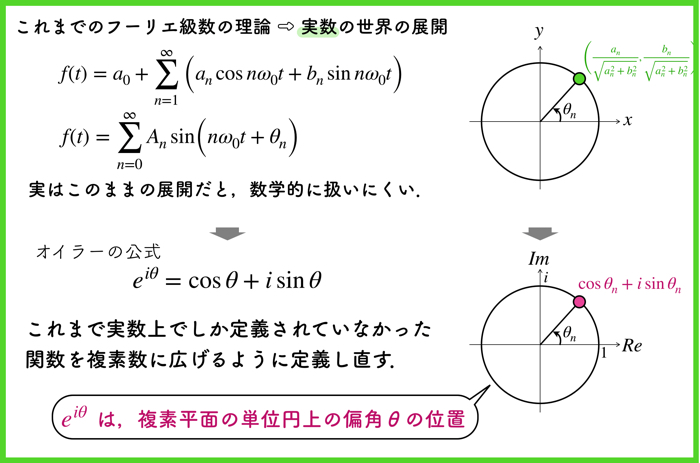
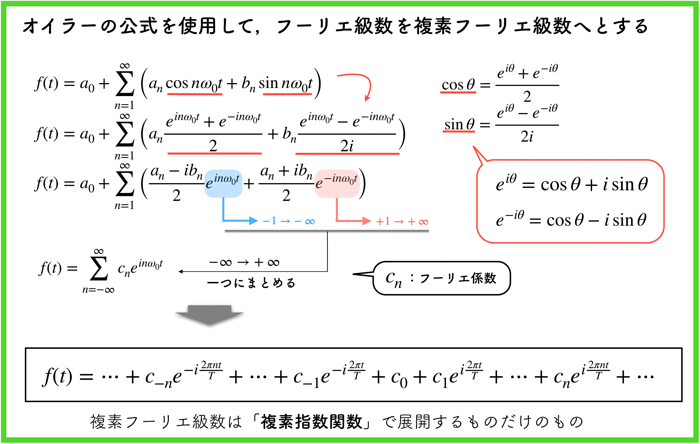
上の二つのスライドは数学のお話です．
オイラーの公式を使用して，「フーリエ級数」から「複素フーリエ級数」へと式変形をします．
数式を見るのがあまり好きではない人でも簡単に理解できると思うので，ちょっと頑張ってじっと見てみてください！

理解が難しい人は，一度ノートに展開式を書いたら理解できるかもしれないです．

複素指数関数\(e\)の直交性

複素指数関数\(e\)で展開する際には，やはり展開された全ての項が直交基底である必要があります．
こちらは，平面ベクトルと同様な性質を持つためすごく理解しやすいです．
ただ，多次元になるので，図示するのはできませんが，概念としては，上の図のようになります．

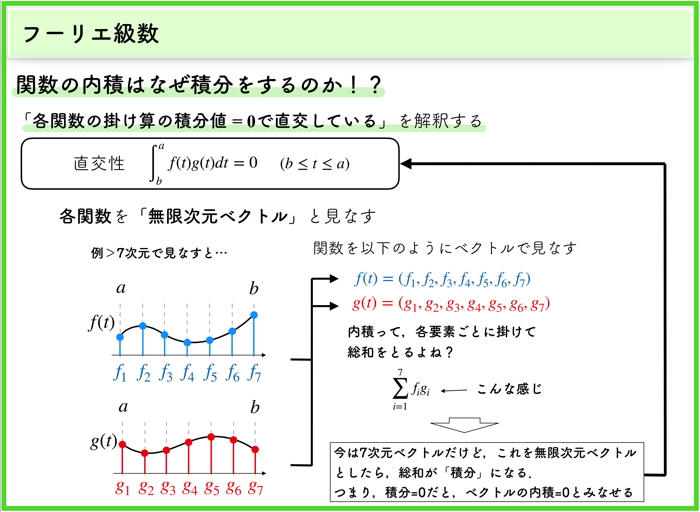
直交基底を示す重要な性質：関数の内積とは

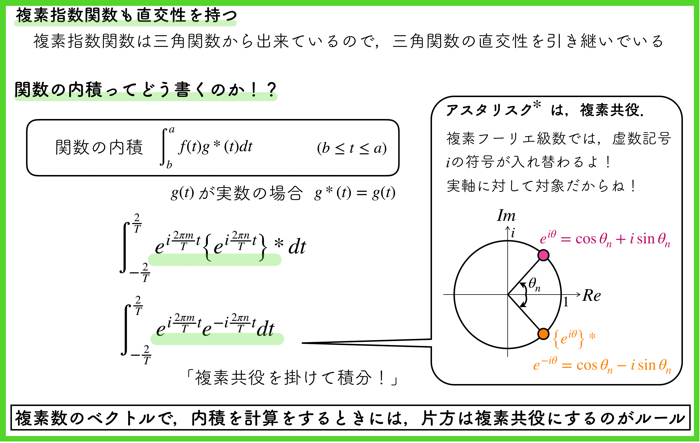
直交基底を示すときは，ベクトルの内積=0を示せばよかったですが，関数の場合は「積の積分」です．
ここら辺は，フーリエ級数と同じなので詳細な説明は前回の記事を見てくださいね！
（【フーリエ解析01】フーリエ級数・直交基底について理解する【動画解説付き】）

ただ，積を取るときには，複素共役を掛けなければいけません．
複素フーリエ級数では，虚数記号\(i\)の符号が入れ替わります．

直交基底について！

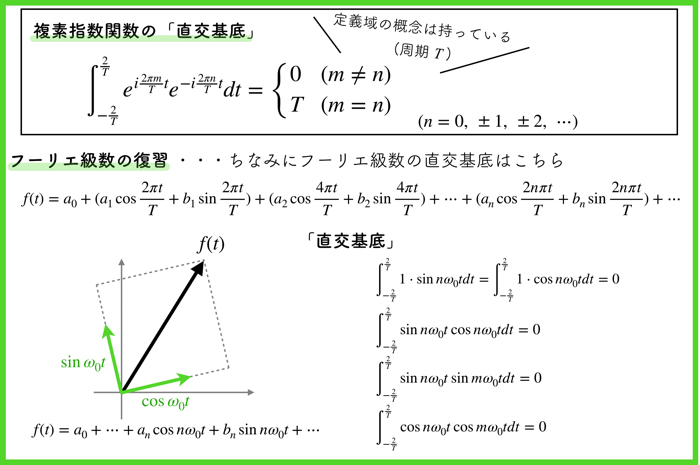
直交基底に関しては，フーリエ級数と同様に，積分をして，複素フーリエ係数を導出できます．
直交基底なので，\(n\)や\(m\)の整数が異なると，0になりますね．
\(n=m\)の場合は，\(\int_{-\frac{2}{T}}^{\frac{2}{T}} e^{i\frac{2\pi m}{T}t} e^{-i\frac{2\pi n}{T}t} dt=T\)が出てきます．

複素フーリエ係数の導出

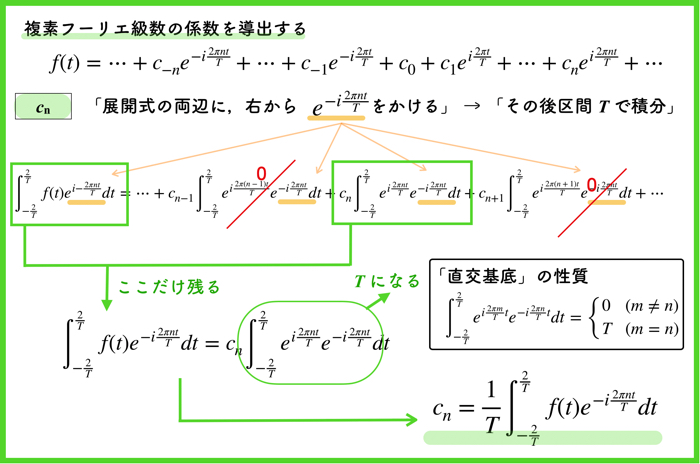
複素フーリエ係数の\(c_n\)を導出する際には，「展開式の両辺に右から複素指数関数\(e^{-\frac{2\pi nt}{T}}\)をかけて，その後，区間\(T\)で積分をする」だけです．

直交基底の性質より，\(n=m\)の場合以外の項は全て消えます．
そうすることで，上記のように\(c_n\)を導出することができます．

複素フーリエ級数のマイナス側の角周波数の理解

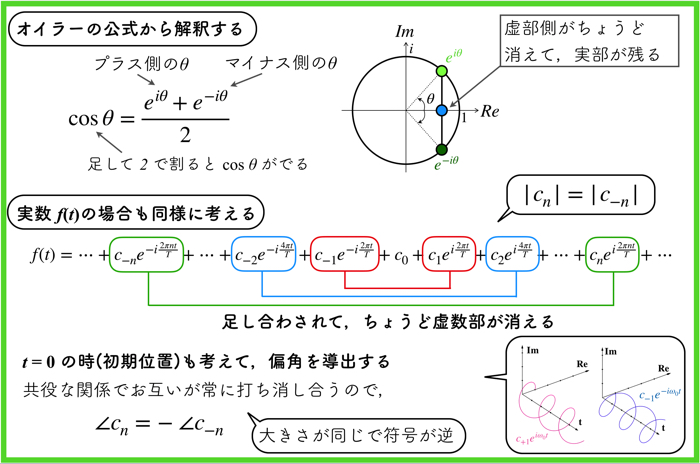
三角関数のみを用いたフーリエ級数と違って，複素フーリエ級数では，マイナス側の周波数が出てきます．
実はこれ，プラス側の周波数とともに計算されて，上手く虚数の値が相殺されるようになっているのです．

オイラーの公式をちょっと覗いてみたら理解度が上がります．
オイラーの公式の\(\cos \theta\)は，プラス側の\(\theta\)とマイナス側の\(\theta\)を足して2で割ることによって，上手く実数へと変換されます．

それと同様に複素フーリエ級数展開のプラス側とマイナス側も機能しています．
そのため，周波数解析を行う際に，考えるべきフーリエ級数は，プラス側だけを見れば良いことになります．

スペクトルの見方

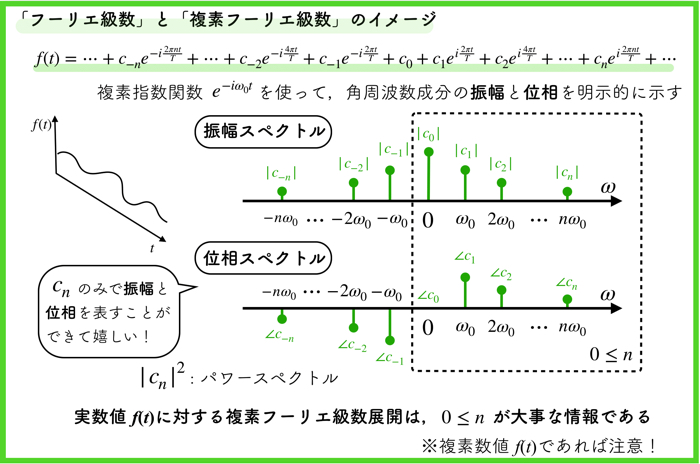
周波数解析を行うときに大事になるのは，周波数成分がどのくらい含まれているかを確認するためのスペクトル分布です．
複素フーリエ級数展開では，プラス側のみの係数\(c_n\)がスペクトルを表します．

• \(|c_n|\)・・・振幅スペクトル
• \(\angle c_n\)・・・位相スペクトル
• \(|c_n|^2\)・・・パワースペクトル

これらをみて，ある関数\(f(t)\)の周波数解析がなされます．
パワースペクトルは，振幅スペクトルを単純に2乗した値です．

このように，複素フーリエ級数展開だと，フーリエ係数\(c_n\)から直接，角周波数成分の振幅や位相を算出することができるので非常に便利です．

動画解説はこちら

練習問題を解いて理解度を高めよう！

解説はこちらです

フーリエ解析：フーリエ級数から高速フーリエ変換までのまとめスライド

参考にした本「道具としてのフーリエ解析」