【フーリエ解析01】フーリエ級数・直交基底について理解する【動画解説付き】

この記事はこんな人にオススメです．

研究で周波数解析をしているけど，内側のアルゴリズムがよく分かっていない人
フーリエ級数や直交基底について詳しく分かっていない人
数学や工学を学ぶ全ての大学生

こんにちは．けんゆー（@kenyu0501_)です．
今日は，フーリエ級数や直交基底についての説明をしていきます．
というのも，信号処理をしている大学生にとっては，周波数解析は日常茶飯事なことだと思いますが，意外と基本的な理屈を知っている人は少ないのではないでしょうか．
ここら辺は，フーリエ解析(高速フーリエ変換)などの重要な超絶基本的な部分になるので，絶対理解しておきたいところになります．

では，早速やっていきましょう！

フーリエ級数とは！？

フーリエ級数は，「あらゆる関数が三角関数の和で表せる」という定理に基づいた素晴らしい関数近似です．

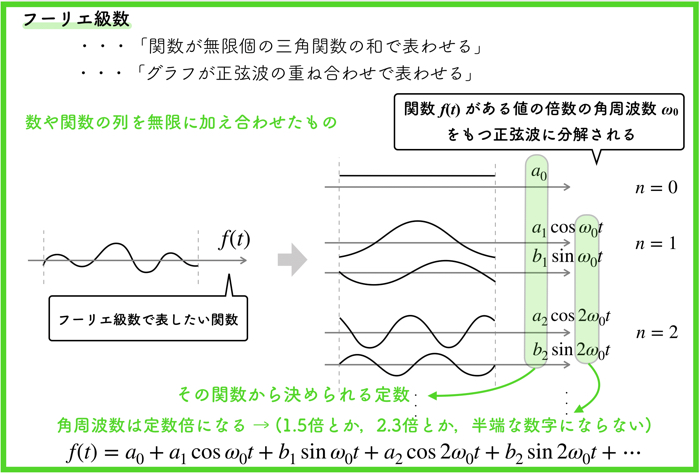
これ，結構すごい展開なんですよね．
あらゆる関数は，三角関数の足し合わせで表すことができるっていう，初見の人は嘘でしょ！？って言いたくなるような定理です．
しかし，実際に，あらゆる周波数成分を持った三角関数(正弦波)を無限に足し合わせることで表現することができるのですね．
素晴らしいです．

重要なこと！基本角周波数の整数倍！

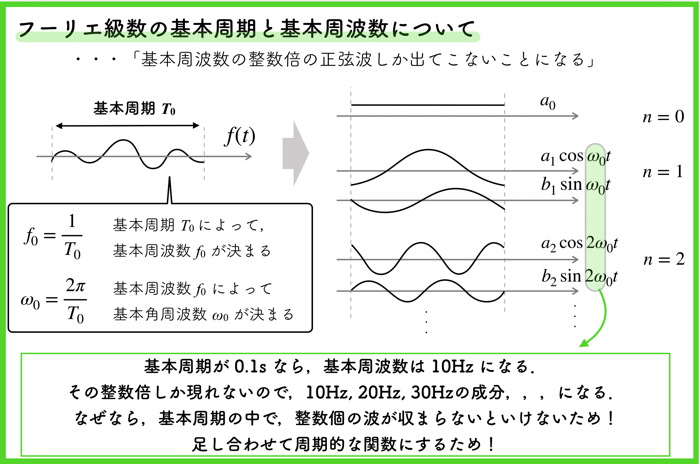
フーリエ級数の場合は，基本周期\(T_0\)が大事です．
基本周期\(T_0\)に従って，基本角周波数\(\omega_0\)が決まります．
フーリエ級数で展開される三角関数の角周波数は基本とされる角周波数\(\omega_0\)の整数倍しか現れないのです．

\(\omega_0\)の2倍，3倍・・・という感じだね！半端な倍数の1.5倍とかは現れないのだね！とびとびの角周波数を持つことになるんだ！

何の役に立つのか！？

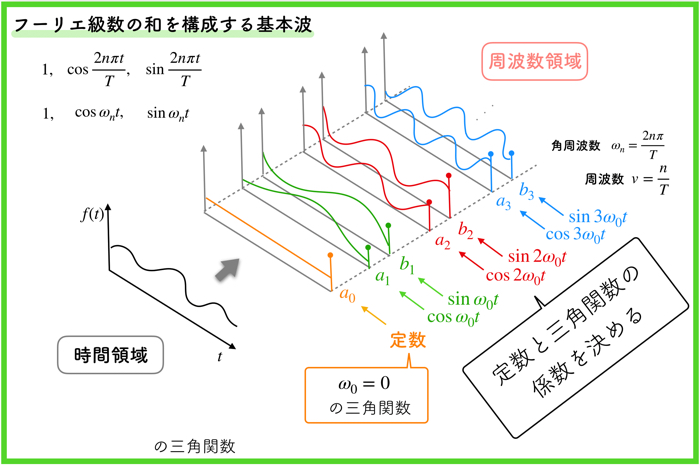
フーリエ変換を日常的に使っている人なら，フーリエ級数のありがたさが分かると思いますが，そういう人は稀です．
詳しく，説明していきましょう．

フーリエ級数とは何かというと，時間的に変動している波に一考察を加えることができる道具です．
例えば，この波は「速い」とか「遅い」とか，

そして，「どう速いのか」などの具体的な数値化を行うことができます．
これは物凄く嬉しいことです．
波の内側の特性を数値化することができるのですね．

フーリエ級数は，いくつかの角周波数を持った正弦波で近似的に表すことでした．
そのため，その角周波数の違う正弦波の量というものが，直接的に元々の関数の支配的(中心的)な波の周波数になりうるのですね．
低周波の三角関数がたくさん入っているから，この波はゆっくりした波だ，みたいな．

復習：波に関する基本用語

テンションアゲアゲで解説してきましたが，波に関する基本的な用語を抑えておかないといけないと思ったので，とりあえず復習しておきます．

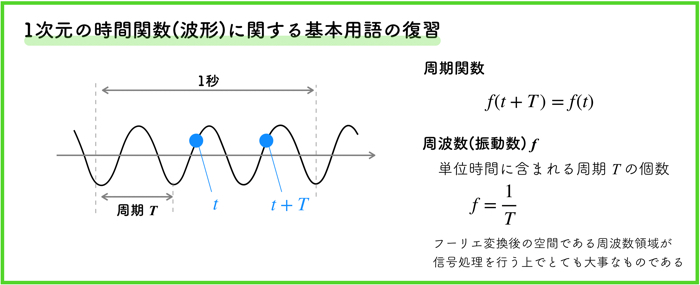
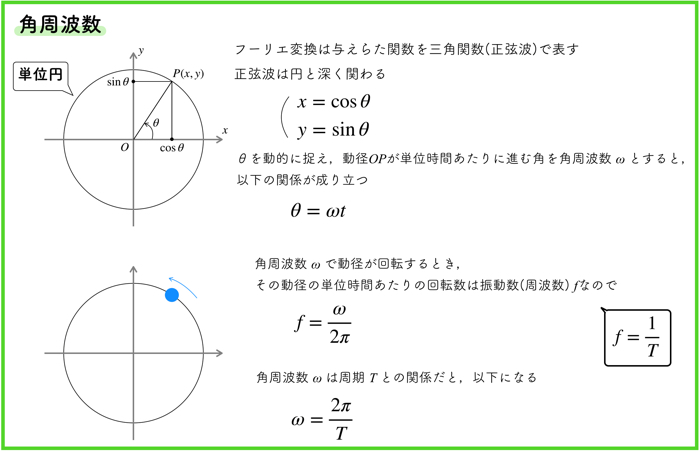
とりあえず，角周波数と周期の関係が把握できたら良しとします．
では先に進みます．
次はフーリエ級数の理論です．

波の基本的なことは絶対に忘れるでないぞ！逆にいうと，これを覚えておけばほとんど理解できてしまうよ！

フーリエ級数の理論

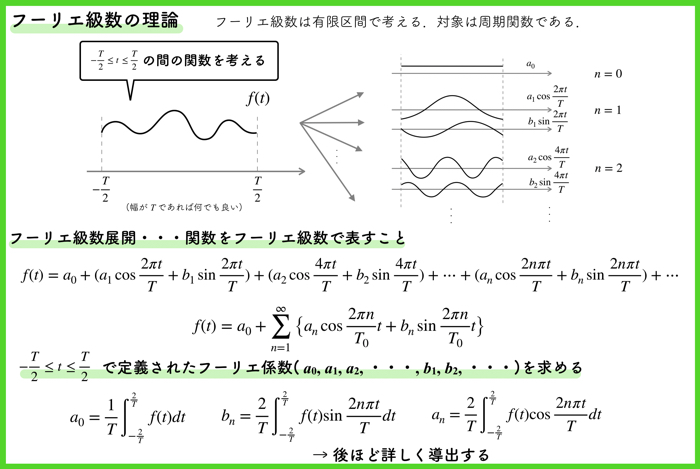
先ほどもちょろっとやりました．
フーリエ級数は，ある関数を，三角関数と直流成分(一定値)で近似することです．
しかしながら，そこには，ある概念が必要です．

区間です．

無限区間では難しいのです．
フーリエ係数という，フーリエ級数で展開した後の各項の係数の数値が定まらなくなるため，区間を有限の範囲に設定する必要があります．
これはだいたい周期\(T\)と呼ばれます．

フーリエ級数は周期\(T\)の周期関数である

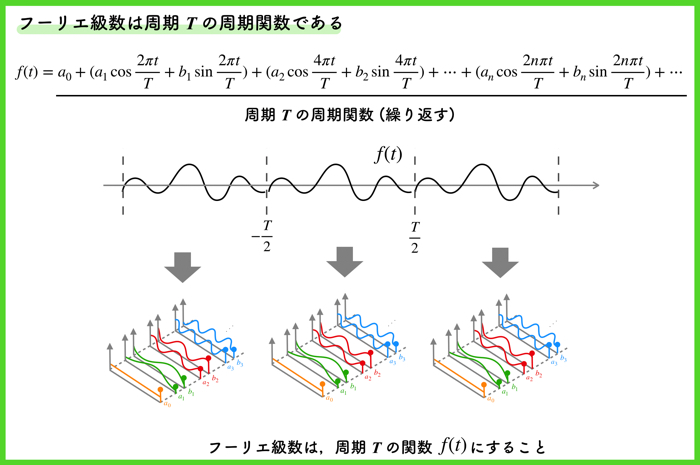
有限区間\(T\)という定まった領域で，関数の近似(フーリエ級数)を行うので，もちろんフーリエ級数で表した関数自体は，周期\(T\)の周期関数になります．
周期関数というのは，周期毎に同じ波形が繰り返す関数ですね．
サイン波とか，コサイン波みたいなやつです．

つまり，ある関数をフーリエ級数で近似的に展開した後の関数というものは，周期\(T\)毎に繰り返される波になるということになります．
これは致し方ないことなのですね．

周期\(T\)毎に繰り返される波になるのだよ！

なんでフーリエ級数で展開できるの！？

どんな関数でも，なぜフーリエ級数で展開できるのかはかなり不思議だと思います．
これには訳があります．
それが次のスライドです．

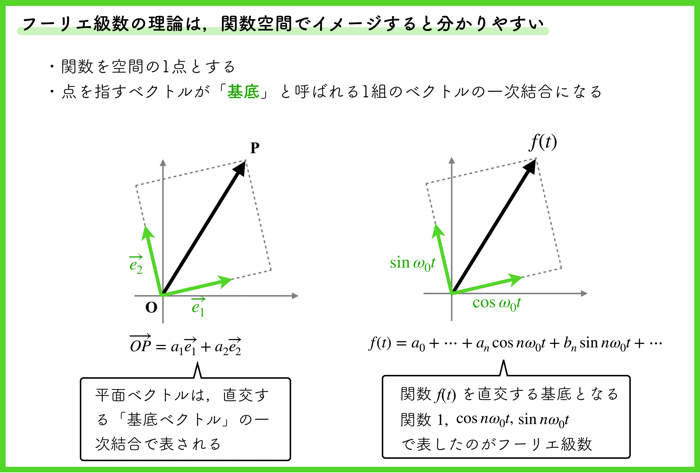
フーリエ級数の理論は，関数空間でイメージすると分かりやすいです．
手順として以下です．

フーリエ級数として展開したい関数を空間の1点とする
点を指すベクトルが「基底」と呼ばれる1組のベクトルの一時結合となる．

平面ベクトルって，各基底ベクトル\(e_1\)，\(e_2\)の線形ベクトルの一次結合で表現できたことは覚えていますか．
上の図の左側の絵のような感じですね．
それが成り立つのは，基底ベクトル\(e_1\)，\(e_2\)が直交しているからですよね．
つまりお互いが90度に直交していて，原点で以外交わらないからですよね．
こういった交わらないものは，座標系として成り立つわけです．
これらは，ベクトル的にいうと，内積＝０という特徴を持っています．

さてさて，
では，右側の関数空間に関しては，どうでしょうか．
実は，フーリエ級数の各展開した項というのは，直交しているのですよね．

これ，，，，控えめに言ってもすごくないすか．

めちゃくちゃ多くの軸(sinとかcos)がある中，全ての軸が直交しているのですね．
これはもちろん2Dでもかけませんし，3Dでもかけません．
数学の世界，代数的なベクトルの世界でしか表現しようがないのです．

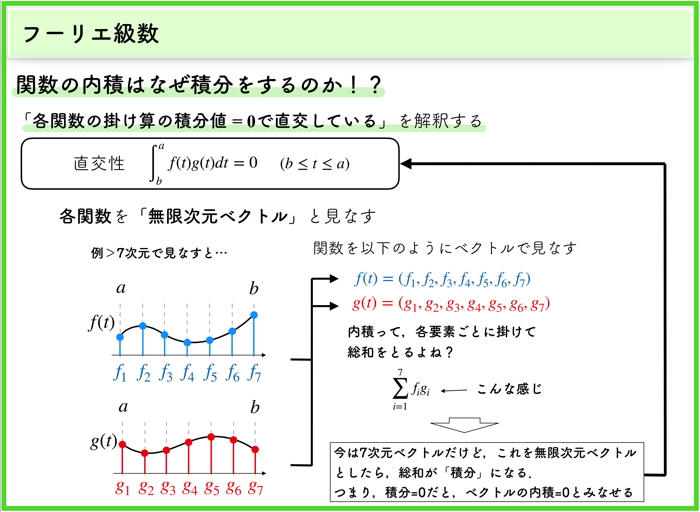
では，関数の内積ってどのように書くの？という疑問が生じると思いますが，これは積分です．
以下のスライドをみてください．

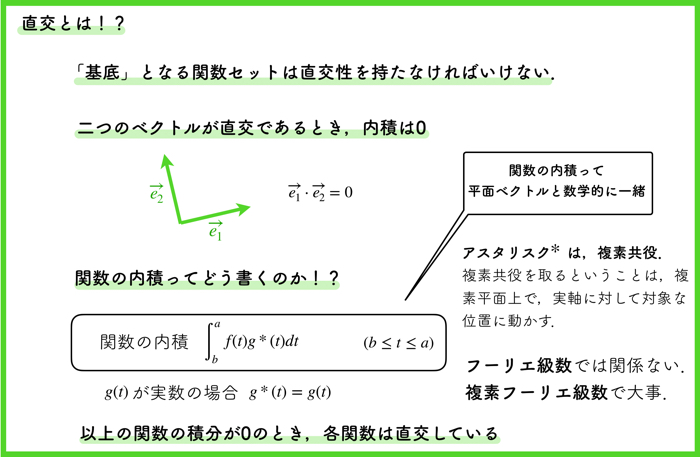
この関数を掛けた積分が内積に相当するので，これが0になれば，フーリエ級数の各項，は直交していると言っても良さそうです．
なぜ内積が積分で表すことができるのか，簡単に理解したい人は，以下のスライドを見てください．

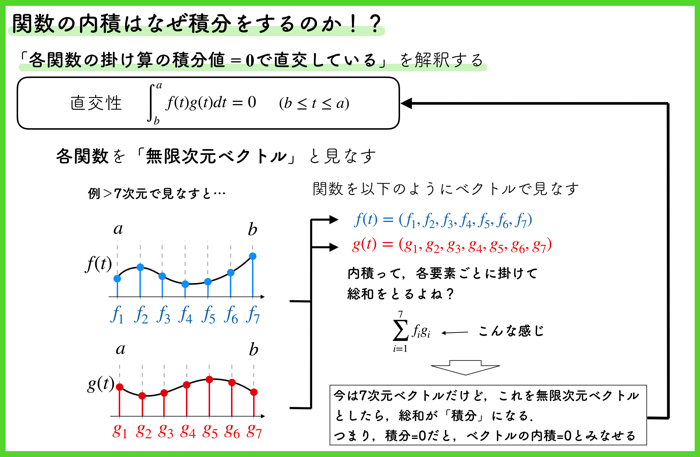
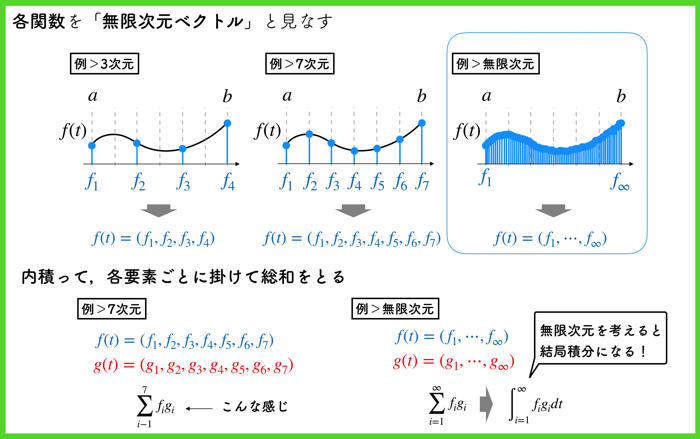
各関数を無限次元のベクトルとして見なせば，積分が内積の計算として見なせそうですよね．
それでもモヤっとしている方や，直交性についてもっと厳密に知りたい方は，こちらの記事をどうぞ．

【フーリエ級数の直交性】関数の積の積分をとるということで内積=0と見なす理由
https://kenyu-life.com/2019/07/11/fourier_naiseki/
この記事はこんな人にオススメです，フーリエ級数や複素フーリエ級数を学習している人積の積分がなぜ内積とみなさ…

数学的な定義だと，これらは直交基底と言われます．

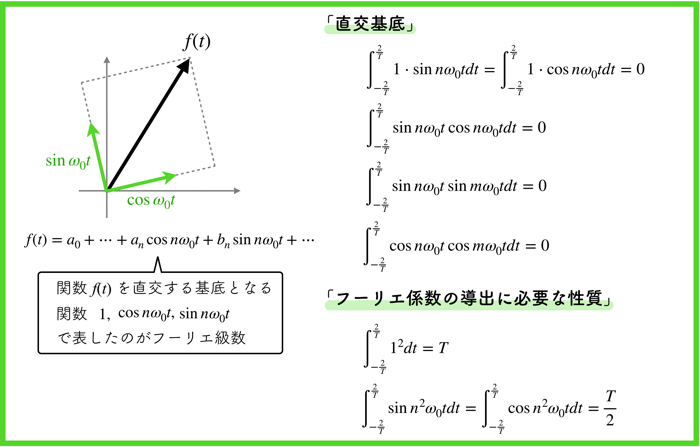
そしてまた，フーリエ係数\(a_0\), \(a_n\), \(b_n\)の導出に必要となる性質も頭に入れておいてください．
これらを用いて，フーリエ係数\(a_0\), \(a_n\), \(b_n\)を導出します，

具体的には，フーリエ級数で展開した後の全ての関数に，cosやsinを掛けて，積分をします．
すると直交基底を満たすものは，全て0になります．
そうすることによって，得たいフーリエ係数\(a_0\), \(a_n\), \(b_n\)が求まります．

各フーリエ級数\(a_0\), \(a_n\), \(b_n\)の導出

\(a_0\)の導出

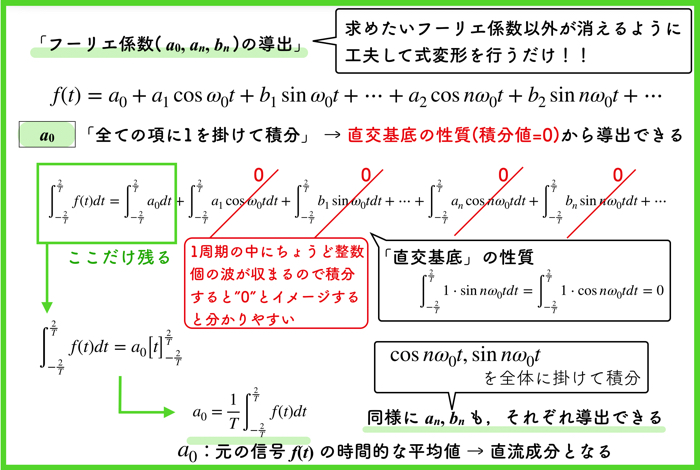
フーリエ係数\(a_0\), \(a_n\), \(b_n\)の導出は，ものすごく簡単です．
求めたいフーリエ係数以外が消えるように工夫して式変形を行うだけです．
\(a_0\)を導出したい場合は，上のスライドのようにします．

ステップ

全ての項に1を賭けて積分する(この積分がベクトルの内積に相当する)
直交基底の性質より，積分をとるとほとんどが0になる．
残った\(a_0\)の項を式変形してフーリエ係数\(a_0\)を導出！

\(a_0\)は元の信号\(f(t)\)の時間的な平均値を表しているね！一定値になるので，電気工学の分野では直流成分と呼ばれているよ！

\(a_n\)の導出

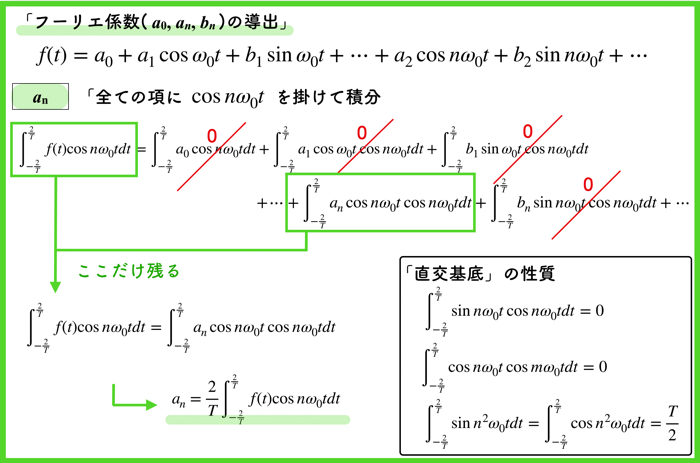
\(a_n\)も\(a_0\)の場合と同様に行います．
しかし，全ての項にかける値は，1ではなく，\(\cos n \omega_0 t \)を掛けます．
その後に全ての項に積分をとる．

そうすると右辺の展開項において，\(a_n\)の項以外は消えます．

\(b_n\)の導出

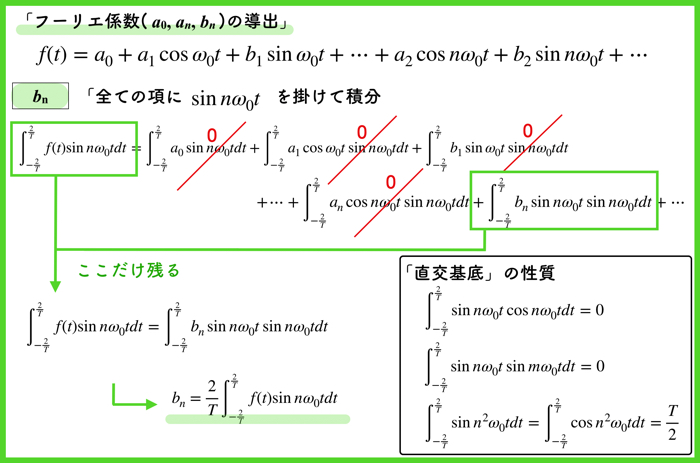
\(b_n\)も同様に導出します．
\(b_n\)を導出した場合は，全ての項に\(\sin n \omega_0 t \)を掛けます．

フーリエ級数の別の表記方法

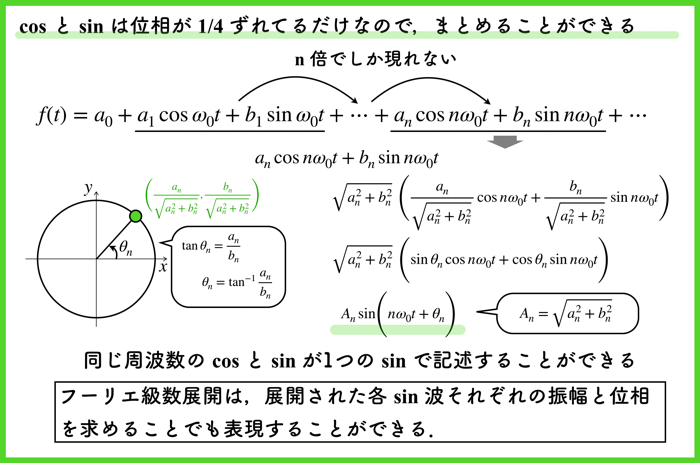
\(\cos\)も\(\sin\)も実は位相が1/4だけずれているだけなので，上のようにまとめることができます．
振動数の振幅の大きさと，位相を導出するために，フーリエ級数展開では\(\cos\)と\(\sin\)を使いましたが，振幅と位相を含んだ形の式であれば\(\sin\)のみでフーリエ級数展開を記述することも可能であります．

動画解説を見たい方は以下の動画がオススメ

フーリエ級数から高速フーリエ変換までのスライドの紹介

ツイッターでもちょっと話題になったフーリエ解析の説明スライドを公開しています．

まとめました！
・フーリエ級数
・複素フーリエ級数
・フーリエ変換
・離散フーリエ変換
・高速フーリエ変換
研究にお役立て下されば幸いです．
ご自由に使ってもらって良いです．
「フーリエ級数」から「高速フーリエ変換」まで全部やります！ https://t.co/5vscc5MXho
— けんゆー@博士課程 (@kenyu0501_) July 8, 2019