- 高速フーリエ変換のアルゴリズムを詳しく理解したい方
- 工学系分野の大学生,大学院生の方
- 信号処理を実際に活用している方
こんにちは.けんゆー(@kenyu0501_)です.
今回は高速フーリエ変換(Fast Fourier Transform :FFT)の説明をしていきます.
といっても,FFTは離散フーリエ変換(Discrete Fourier Transform: DFT)の計算の仕組みを上手く改良して,計算速度を速くするといったシンプルなものです.
なので,基本的には,DFTのアルゴリズムを理解していたら,すぐに理解することができます.
DFTの復習
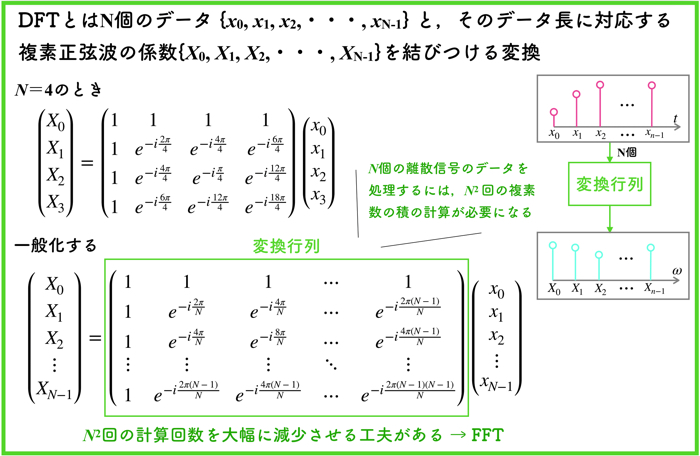
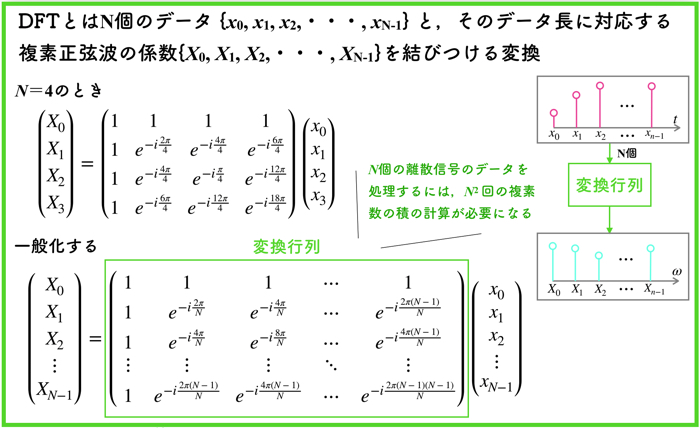
DFTとは,\(N\)個のディジタル信号 \({x_0, x_1, x_2, \cdots, x_{N-1}}\)と,そのデータ長に対応する複素正弦波の係数\({X_0, X_1, X_2, \cdots, X_{N-1}}\)を結びつける変換になります.
また,\(N\)個のディジタル信号を処理する場合,\(N^2\)回の複素数の積の計算が必要になります.
DFTについてはこちらの記事に詳しく記載しています.
この記事はこんな人にオススメです. 離散フーリエ変換について詳しく知りたい人 高速フーリエ変換(FFT)を使用…
FFTの概要について
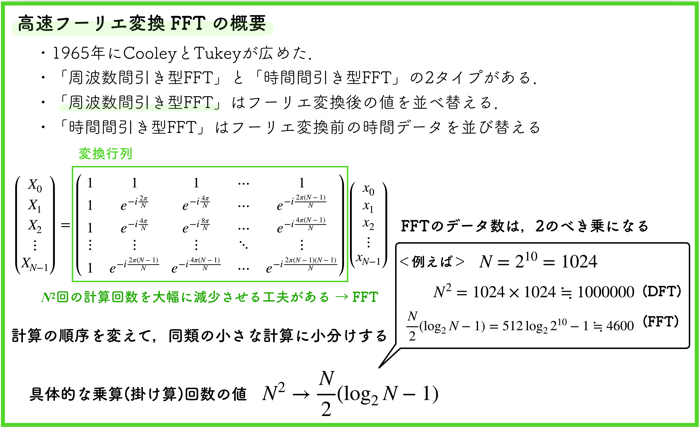
- 1965年にCooleyとTurkeyが広めた.
- 「周波数間引き型FFT」と「時間間引き型FFT」の二つのタイプがある.
- 「周波数間引き型FFT」はフーリエ変換後の値を並べ替える.
- 「時間間引き型FFT」はフーリエ変換前の時間データを並び替える.
- FFTを行う際は,データ数を2のべき乗に揃えないといけない.
- DFTでは\(N^2\)回だった計算回数が,\(\frac{N}{2} (\log_2N-1)\)回まで減るので計算が速くなる
今回説明していくFFTのは,「周波数間引き型FFT」についてやっていきます.
FFTを行うと,DFTよりも計算スピードが速くなるといいましたが,具体的にどのくらい速くなるかというのを上の図で確認してみましょう.
データ数が1024点の場合,FFTは DFTに比べて,200倍以上も速く計算ができることがわかります
また,このブログ記事では,FFTを理解していくために以下の4つを確認していきます.

データが2のべき乗に従わないといけないので,データ数が2, 4, 8の場合を考えます.
その後,バタフライ演算や,ビットリバースの概念について具体的な数値を交えながら解説していきます.
回転因子を導入する
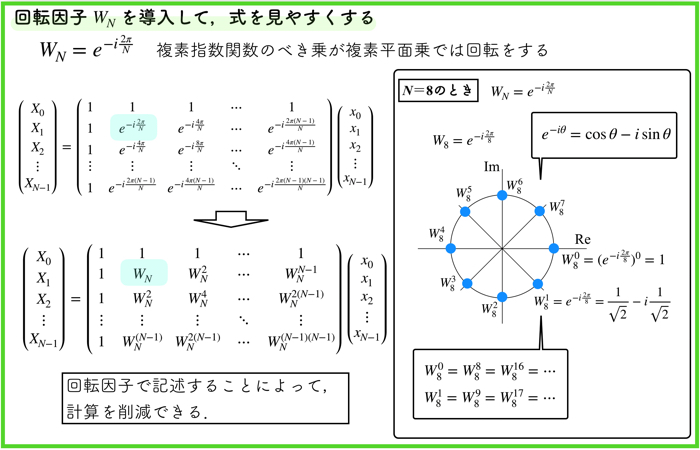
まず初めに,回転因子\(W_N=\exp^{-I\frac{2\pi}{N}}\)というものを導入して,式を見やすくします.
この回転因子というものは,複素指数関数のべき乗が,複素平面上では回転する性質を持っているので,回転因子という名前がついています.
N=8の時の回転因子を見てみてください.
この回転因子を8乗すると,単位円乗を一周して,元の値である0乗に帰ってくることがわかります.
このようにして,計算を削減するために式変形を行っておきます.
回転因子の導入に関して
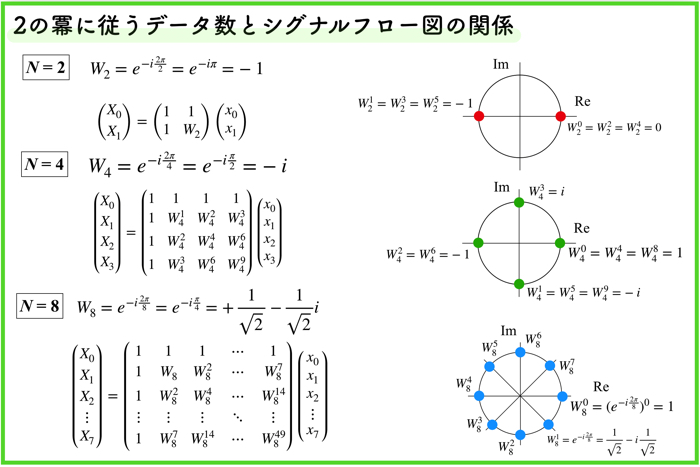
先ほどの回転因子を導入した式変形に関して,N=2,4,8の場合を取り上げておきます.
そうすると上の図のようになるかと思います.
バタフライ演算とシグナルフローについて
FFTの計算は,バタフライ演算という以下の方法をを知っておくと理解が早いです.
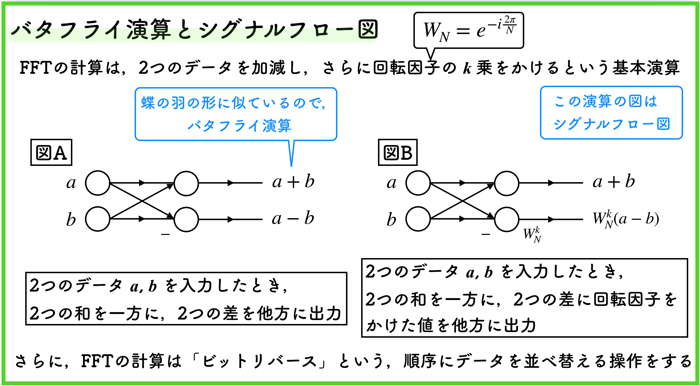
FFTの計算は,2のデータを加減し,さらに回転因子のk乗をかけるという基本演算に基づきます.
そのため,以上のシグナルフロー図で示したバタフライ演算が行われます.
バタフライ演算は,上の示した図のように,計算が蝶の羽の形に似ているのでその名前が付けられました.なんかおしゃれですね.
また,FFTの計算は,「ビットリバース」に基づいてデータを並び替える必要がありますが,それはまた後ほど説明します.
では実際に,バタフライ演算の具体例を見ていきましょう!
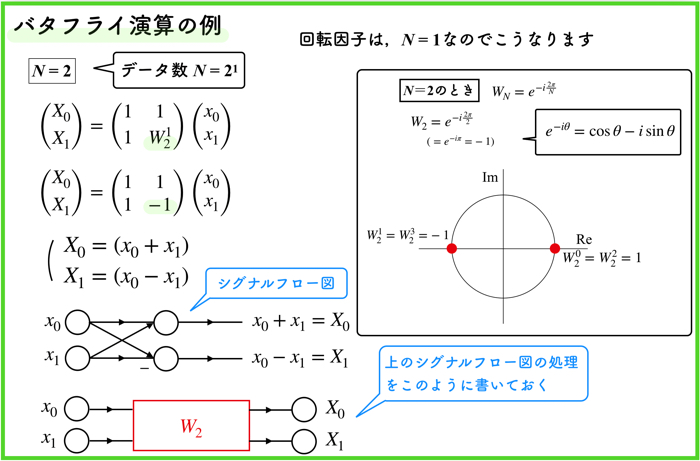
バタフライ演算の例 N=2の場合
N=4の時の例
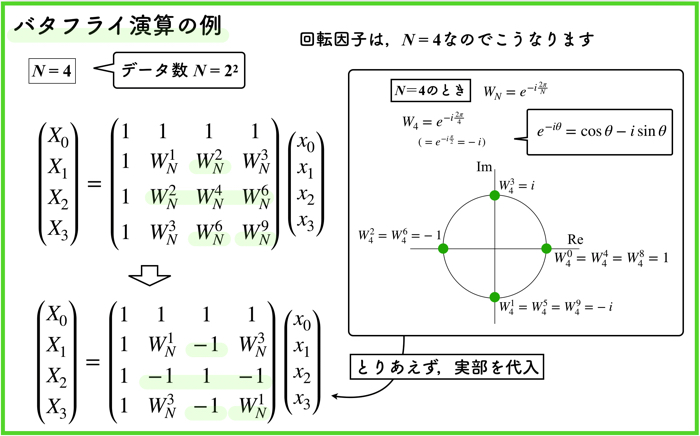
N=4の時は,ビットリバースを行なって,式変形を行う必要があります.
ビットリバースは,ディジタルデータの数値番号を一度2進数に直して,順番を逆転させたものです.
以下の図をご覧ください.
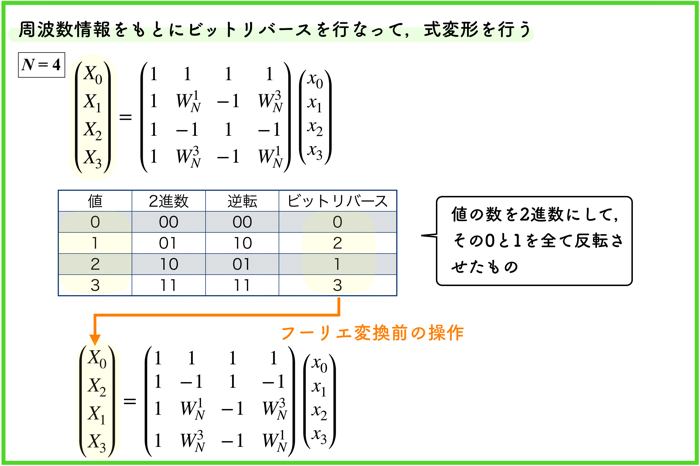
そうすると,以下のようになります.

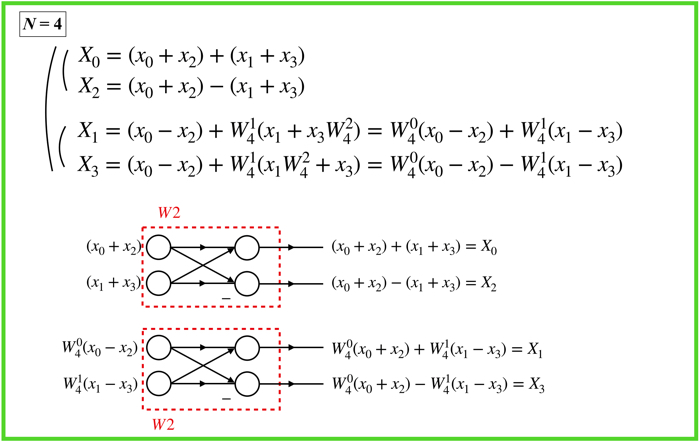
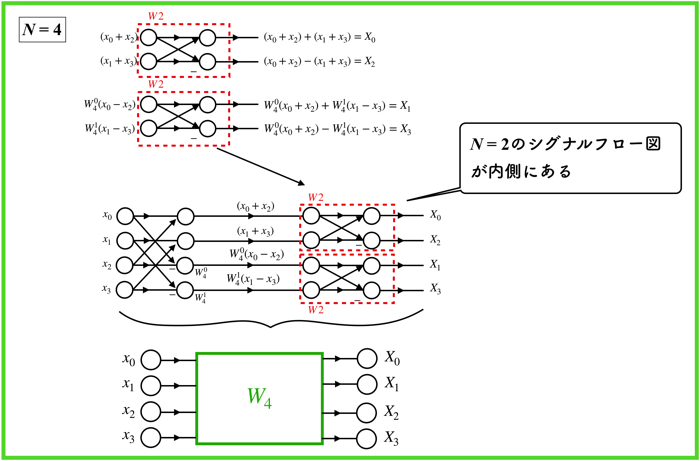
以上がN=4の場合のFFTについてでした.
N=4の場合のFFTの内側には,N=2の場合のFFTが入っていますね.
N=8の場合の例
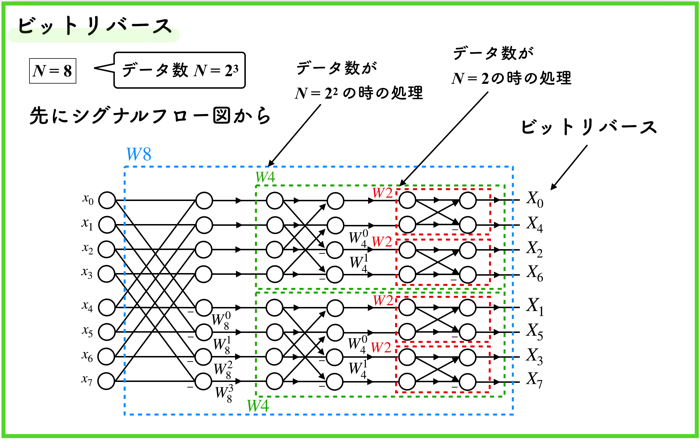
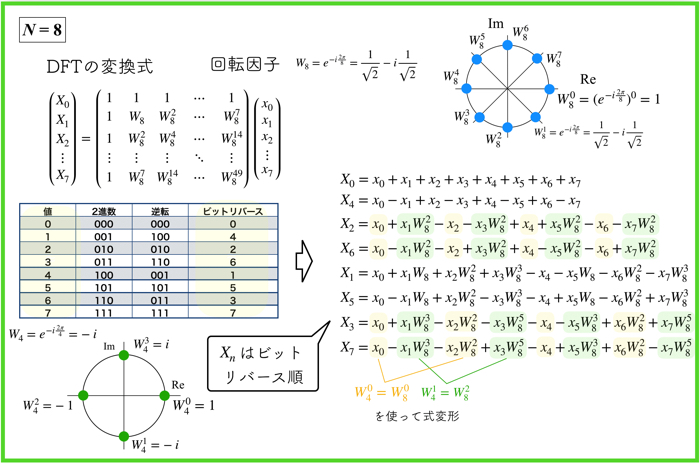
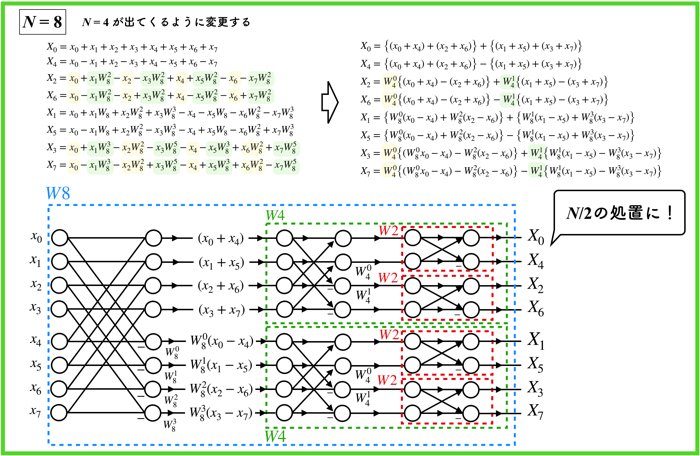
すごく複雑な式になっていますが,ギリギリ追いかけることができますね!皆さんもじっくり確認してみてください.
FFTの一般化を行う
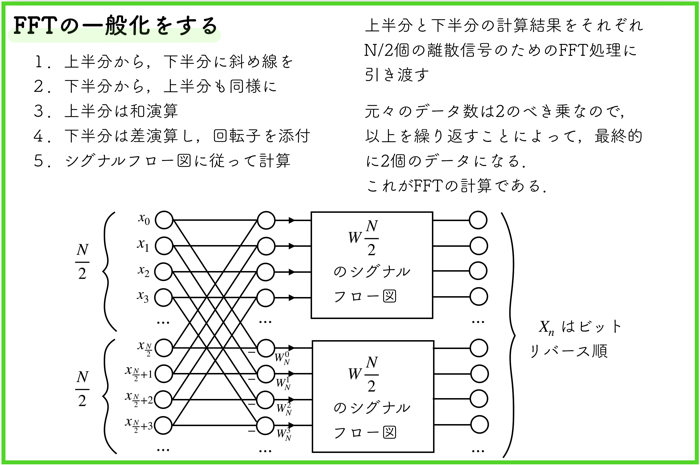
N=8のアルゴリズムで大方予想がたったと思いますが,FFTの一般化は上の図のようになります.
データを半分に分けて,上半分と下半分を上手くバタフライ演算していく,というのを繰り返していくのですね.
これがFFTの計算の仕組みです.
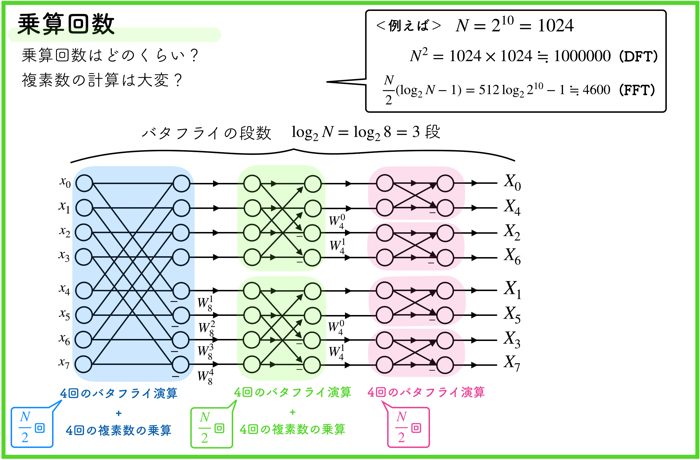
乗算回数はどのくらいになるの?

FFTの気になる乗算回数ですが,DFTでは\(N^2\)回だった計算回数が,\(\frac{N}{2} \log_2N-1\)回まで減ります.具体的な数値を入れて示したのが上の図です.
コンピュータの演算コストというのは,足し算と引き算に比べて,掛け算がものすごく大きいです.
掛け算だと桁が上がるので当然ですね.
なので,掛け算の数に従って,計算コストが高くなっていくのですね.
この掛け算の数が,FFTだとかなり小さくなって,\(\frac{N}{2}( \log_2N-1)\)回になっていきます.




非常にわかりやすかったです。別の記事も楽しみにしています!