- ガウスカーネル(RBFカーネル)，多項式カーネル，シグモイドカーネルを試す．
- irisのデータセットを使用する．
- プログラムの公開（任意でハイパーパラメータや使用するirisデータを変更できるようにしている）．
こんにちは．けんゆー（@kenyu0501_)です．
この記事では，サポートベクターマシンで2値問題を解くことを行います．
サポートベクターマシンが全く分からないという方は以下をさらっと見ておくことをお勧めします．
(参考：サポートベクターマシン(SVM)とは？〜基本からpython実装まで〜)
サポートベクターマシンでは，クラス分けをする際に，直線(もしくは超平面)での線形分離が不可能な場合があります．
その時は，特徴量を高次元へと写像して上手く分離ができる状態まで持っていきます．
しかし，入力する特徴量がもともと持っている次元数が，爆発的に増えるため，計算量も爆発的に増えます．
そのため，カーネルトリックという工夫を凝らして，マージン最大化の最適化問題を解くということをやるのでしたね！
(マージン最大化とは，各クラスのサポートベクトル(点)と分離超平面との距離を最大化すること)
今回は，irisデータセットを使って，各種カーネル関数がどのような分離超平面を形成するのか，について見ていきます．
使うデータ(irisデータセット)の確認
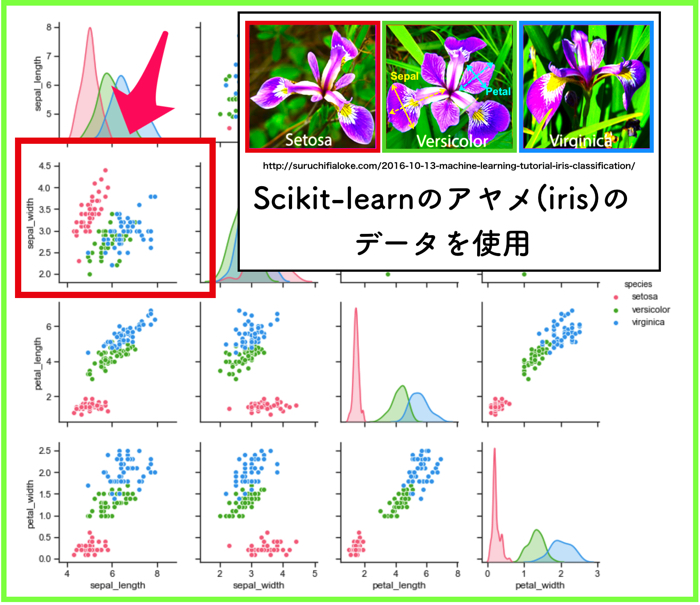irisデータセットが具体的に何か分からないという方は，こちらの記事をご覧ください．
（参考：iris(アヤメ)のデータセットをpandasとseabornを使って可視化する．）
今回は，irisデータのsepal_width とsepal_lengthのデータを使います．がく片の幅と長さですね！
(プログラム内では変更できるようになっています)
サポートベクターマシンで分離をしますが，線形分離可能なデータと線形分離不可能なデータを扱います．
＜線形分離可能なデータ＞
- setosa と versicolor を使う．
＜線形分離不可能なデータ＞
- versicolor と virginica を使う．
狙いとしては，線形分離不可能なデータを分離する際に，カーネル関数の種類によってどのような分離曲線が書かれるのか！ということを確認していきたいのです．
もちろん，ハイパーパラメータによって，分離線は違うと思いますが，ざっくりと知見を得ることは可能です．
試すカーネル関数について
上記の4つのパターンを比較します．
- カーネル関数なし
- ガウスカーネル $$K(x_i, x_j) = \exp (-\gamma||x_i – x_j||^2)$$
- 多項式カーネル $$K(x_i, x_j) = (x_i^T x_j+c)^d$$
- シグモイドカーネル $$K(x_i, x_j) = \tanh (bx_i^T x_j+c)$$
結果は！？
線形分離可能な場合
setosa と versicolor の結果です．
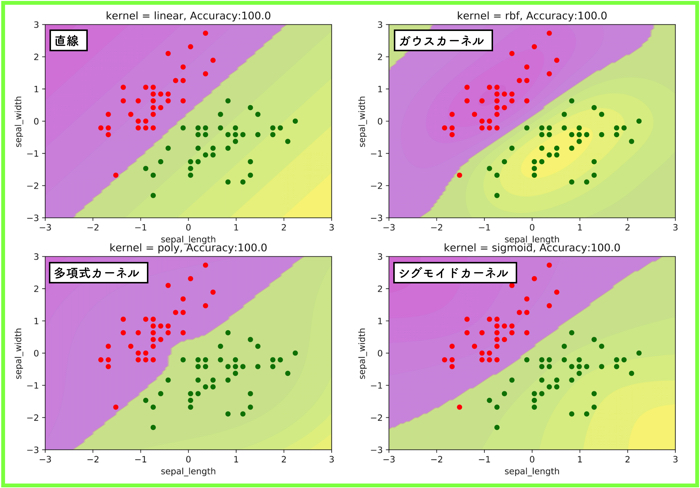
setosa と versicolor は各50サンプルずつあるのですが，トレーニングデータ(教師)に80%を使って，残りの20%をテストデータに使っています．
とりあえず，この線形分離可能なデータの分類は，テストデータで汎化性能を見た結果，正解率は100%になりました．
(当たり前ですね)
交差検証などはやっておらず，ハイパーパラメーターは以下です．
(γ=1，c=1, d=3，コスト関数C=1（ソフトマージン）)
もちろん，どのカーネルを見てもあまり違いがわかりにくいです．
(直線に近い)
ほとんど直線みたいな結果だね！
線形分離不可能な場合
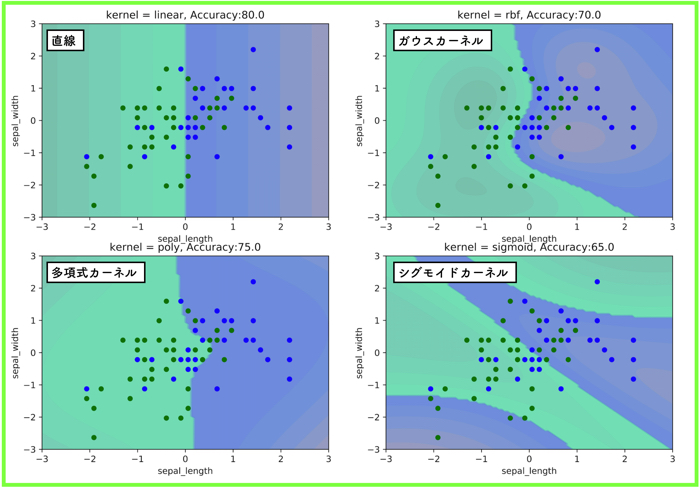
versicolor と virginica の結果です．
ハイパーパラメータなどはそのままで，扱うデータを変えたものです．
カーネル関数による形状を確認したかったので，交差検証などはやっていないのです．
正解率で一番大きいのは，何も手を加えていない直線っていうもの皮肉な話です．
そこらへんは，ハイパーパラメータを調整したりして検討しなければいけません．
ガウスカーネルの形状は，データが密集している箇所に局所的に領域があるみたいだね！
多項式カーネルの形状は，ある程度分布全体のばらつきを考慮して境界が歪んでいる感じだ！
シグモイドカーネルの形状は，写像後の特徴空間で急激な変動があったのか，境界面がいくつもできているね！
自分でプログラムを触ってみて，自分で扱うデータ点を変更してみてねー！
プログラム
作成したプログラムも載せておきます．
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 | #!/usr/bin/env python3 # -*- coding: utf-8 -*- """ Created on Sun May 12 10:26:57 2019 @author: ueharakenyuu """ import pandas as pd import mglearn import seaborn as sns import numpy as np import matplotlib.pyplot as plt from sklearn.model_selection import train_test_split from sklearn.preprocessing import StandardScaler from sklearn.svm import SVC from sklearn.datasets import load_iris iris_dataset = load_iris() ############irisのデータの確認として################### print("Keys of iris_dataset: \n{}" .format(iris_dataset.keys())) print("First five columns of data: {}" .format(iris_dataset['data'][:5])) print("Shape of data: {}" .format(iris_dataset['data'].shape)) print(iris_dataset['DESCR'][:193] + "\n...") print("Feature names: {}" .format(iris_dataset['feature_names'])) print("First five columns of target: {}" .format(iris_dataset['target'][:5])) print("Filename: {}" .format(iris_dataset['filename'])) print("Target names: {}" .format(iris_dataset['target_names'])) ############pandasを使ったデータ全体の図示################### #使うときには，コメントアウトを外して！ """ iris_dataframe = pd.DataFrame(data=iris_dataset.data, columns=iris_dataset.feature_names) print(iris_dataframe.head()) iris_datalabel = pd.Series(data=iris_dataset.target) print(iris_datalabel.head()) grr = pd.plotting.scatter_matrix(iris_dataframe, c=iris_datalabel, label=iris_dataset.feature_names, \ figsize=(8,8), marker = 'o', hist_kwds = {'bins':20}, s=60, alpha=.8, cmap = mglearn.cm3) plt.show() """ ############seabornを使ったデータ全体の図示################### #使うときには，コメントアウトを外して！ """ iris_dataset = sns.load_dataset("iris") sns.pairplot(iris_dataset, hue='species', palette="husl").savefig('seaborn_iris.png') """ ############irisデータの取り込み################### #特徴量のセットを変数Xに，ターゲットを変数yに X = iris_dataset.data y = iris_dataset.target #'setosa'=0 'versicolor'=1 'virginica'=2 X_sl = np.vstack((X[:, :1])) #sepal lengthのみを取得 X_sw = np.vstack((X[:, 1:2])) #sepal widthのみを取得 X_pl = np.vstack((X[:, 2:3])) #petal lengthのみを取得 X_pw = np.vstack((X[:, 3:4])) #petal widthのみを取得 X = np.hstack((X_sl,X_sw)) #sepal lengthとpetal widthのみを扱う X = X[y!=2] #'virginica'=2を排除 y = y[y!=2] #'virginica'=2を排除 scaler = StandardScaler() #標準化を行います． X = scaler.fit_transform(X) ############学習データとテストデータを分ける################### X_train, X_test, y_train, y_test = train_test_split(X, y, random_state = 0) print("X_train stape: {}".format(X_train.shape)) print("y_train stape: {}".format(y_train.shape)) print("X_test stape: {}".format(X_test.shape)) #----------グラフ描写用の関数---------------# def plot_decision_function(model): _x0 = np.linspace(-3.0, 3.0, 100) _x1 = np.linspace(-3.0, 3.0, 100) x0, x1 = np.meshgrid(_x0, _x1) X = np.c_[x0.ravel(), x1.ravel()] y_pred = model.predict(X).reshape(x0.shape) y_decision = model.decision_function(X).reshape(x0.shape) plt.contourf(x0, x1, y_pred, cmap='spring', alpha=0.4) plt.contourf(x0, x1, y_decision,levels=10, alpha=0.2) def plot_dataset(X,y): plt.plot(X[:, 0][y==0], X[:, 1][y==0], "ro", ms=5) plt.plot(X[:, 0][y==1], X[:, 1][y==1], "go", ms=5) plt.xlabel("sepal_length") plt.ylabel("sepal_width") #---------------------------------------# #----4つのパターンを試す-------------# plt.figure(figsize=(13,9)) kernel_names= ['linear','rbf','poly','sigmoid'] i=0 for kernel_name in kernel_names: X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, test_size = 0.2, random_state=0) svm = SVC(kernel = kernel_name) svm.fit(X_train,y_train) R = svm.predict(X_test) total = len(X_test) success = sum(R == y_test) plt.subplot(221 + i) plot_decision_function(svm) plot_dataset(X_train,y_train) plt.title("kernel = {}, Accuracy:{:.1f}".format(kernel_name, 100.0*success/total)) i += 1 #plt.show() plt.savefig('output.png',dpi=900) #----4つのパターンを試す-------------# |
そのまま回したら，線形分離可能な場合の4つのグラフが出てくると思うよ！
プログラムの仕組みを丁寧に説明していきます．
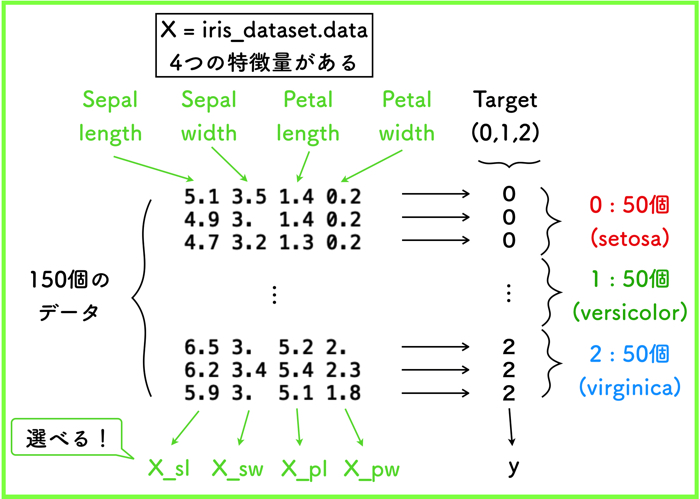
どの特徴量を使うのか
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | ############irisデータの取り込み################### #特徴量のセットを変数Xに，ターゲットを変数yに X = iris_dataset.data y = iris_dataset.target #'setosa'=0 'versicolor'=1 'virginica'=2 X_sl = np.vstack((X[:, :1])) #sepal lengthのみを取得 X_sw = np.vstack((X[:, 1:2])) #sepal widthのみを取得 X_pl = np.vstack((X[:, 2:3])) #petal lengthのみを取得 X_pw = np.vstack((X[:, 3:4])) #petal widthのみを取得 X = np.hstack((X_sl,X_sw)) #sepal lengthとpetal widthのみを扱う X = X[y!=2] #'virginica'=2を排除 y = y[y!=2] #'virginica'=2を排除 scaler = StandardScaler() #標準化を行います． X = scaler.fit_transform(X) |
今回，iris_datasetには，4つの特徴量があると思いますが，SVMで使用するのは，2つなので選択できるようにしました．
最終的に，X=np.hstack((X_sl,X_sw))とすると，Sepal lengthとSepal widthのみを取り扱うことになります．
また，2値問題を解くので，ターゲットも2つで良いです．
ターゲットは0,1,2の3種類(それぞれ50個ずつのデータ)があるので，１つのターゲット群を除外します．
上のプログラムの例では，virginicaを除外するので，X=X[y!=2]としています．
最終的に，0と1のデータに成形された後に，標準化(StandardScaler)を行います．
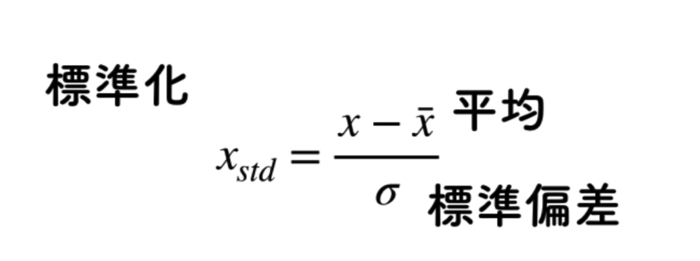
標準化をするとデータの群が以下のようになります．
- 平均→0
- 分散(標準偏差)→1
全てのデータを平均値で引いて，引いたデータに対して，標準偏差で割るためです．
1 2 3 4 5 | def plot_dataset(X,y): plt.plot(X[:, 0][y==0], X[:, 1][y==0], "ro", ms=5) plt.plot(X[:, 0][y==1], X[:, 1][y==1], "go", ms=5) plt.xlabel("sepal_length") plt.ylabel("sepal_width") |
また，グラフ描写用の関数のターゲットの値も揃えてください．
ここでは今回，ターゲットのyが0と1を使用しているので，y==0とy==1です．
(ターゲットが変わるとyの値も変えてください)
これで，必要な設定はほとんど済んだと思います
svmのハイパーパラメータの設定
カーネル関数は，以下4つの場合で試しています．
(１つは線形)
1 | kernel_names= ['linear','rbf','poly','sigmoid'] |
これは，全てデフォルトの値を使用しています．
sklearnのライブラリを使用してますね！
1 | from sklearn.svm import SVC |
線形分離不可能なデータに対して，SVMをとりあえず実装してみたい人はどうぞ！
ガウス(rbf)カーネルについては，以下の記事でチューニングする方法を書いています．
(参考：rbfカーネルのハイパーパラメータをグリッドサーチとベイズ最適化で探す)
