
- 脳神経の活動に対してどのように数学的アプローチを行うのか.
- 様々なモデルについて学べる.
- 決定論,確率論的制御についての理解など.
こんにちは.けんゆー(@kenyu0501_)です.
2019年6月に出版された「計算論的神経科学」を読んだのですが,かなり読み応えがありましたので,ざっとレビュー記事を書いておこうと思います.
読んだ感想を一言で言うと,「研究を中断してでも,早やめに読みたかった!」です.
脳などの神経系の研究をされている方で,数学モデルを構築したり,実際に実験をしていたりされている方は多いと思います.
おいらもその中の一人なのですが,そういった方には特におすすめです.
本を読んだレビュー:個人的な私情も挟みつつ.

おいらの研究の分野と非常に近しいので,私情を挟むよ!
この計算論的神経科学では,以下の3つの事柄を目的としています.
- 脳の計算理論 (脳の計算すべき目的とは?)
- 表現とアルゴリズム (計算のためにどのような表現とアルゴリズムを用いているか)
- 実装 (神経系にどのように実装するか)
これらの目的を,神経活動と行動のモデル化を通して理解していくという.
おいらも実際に,脳波とその背景にある規則性を数学モデルで解明しようとしているうちの一人です.
ここで大事なことは,脳の現象と数学をいかに対応させるのか,ということが研究の課題だったりします.
そのためには,上の3つの事柄でもあげたように.
「何の目的のために,数式を計算するのか」とか,「なぜこの変数が必要なのか」などをきちんと咀嚼していかなければいけません.
おいらでも,そのような問いを日常的に持って,研究をしているわけですが,この本を読んでより一層,研究意欲が増しました.
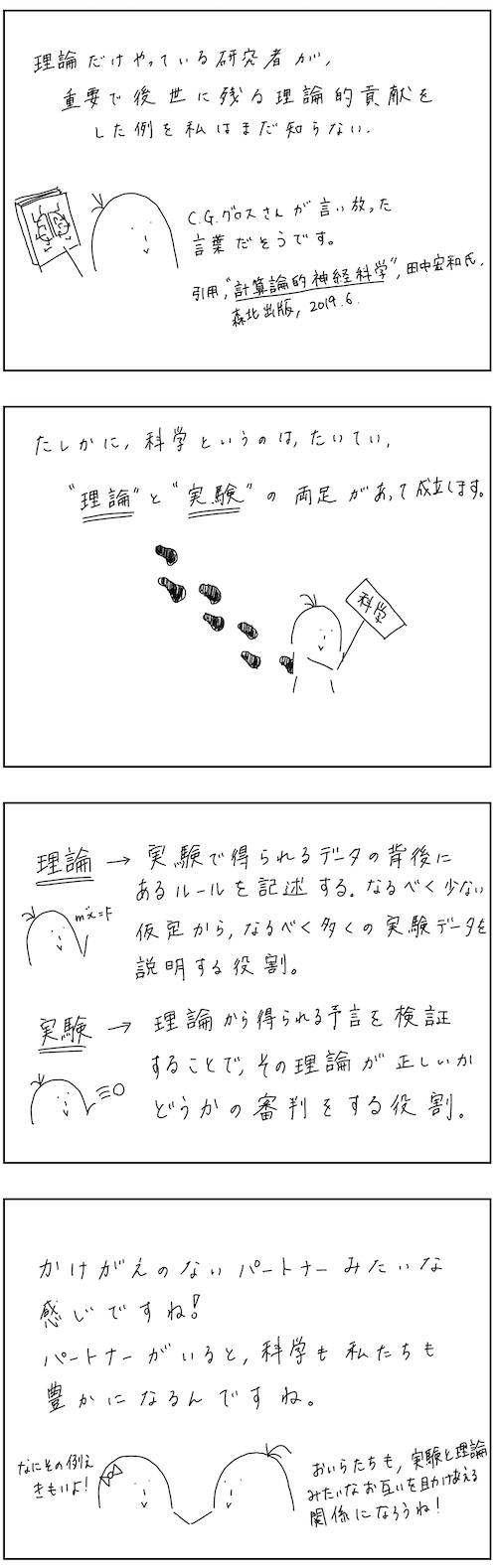
そういった目的意識が具体的に明記されているので,「なるほど!」と思うと同時に,理論や実験の重要性も再確認できました.
神経学を学んでいる人で,実験的アプローチって本当に限界があるの?と思っている方や,理論を重視した定量的アプローチってどのくらい重要なの?と思っている方に是非読んでほしい一冊です.

特に第0章こそ,読み応えがあるよ!
本の目次をざっくりと紹介
- 第0章 計算論的計算科学
ーなぜ脳科学に計算論が必要なのかー - 第1章 身体運動の基礎
ーキネマティックス・ダイナミクス・座標変換,それらの脳内表現ー - 第2章 決定論的最適制御
ー運動の背後に潜む最適化の計算原理ー - 第3章 状態空間モデル
ー運動過程と観測過程のモデル化ー - 第4章 最適推定
ー感覚入力からの外界再構成ー - 第5章 確率論的最適制御
ーノイズ下でも正確な運動を可能にする制御ー - 第6章 強化学習
ー報酬に基づく運動学習ー - 第7章 システム同定
ー運動適応過程のリバースエンジニアリングー - 第8章 次元縮約と成分分析
ー脳のなかの真の自由度ー - 第9章 デコーディングとブレイン・コンピュータ・インターフェース
ー脳の情報表現を読み取るー - 第10章 小脳の計算モデル



目次だけ抜粋しましたけど,ぜひとも本書「計算論的神経科学」を一読してもらいたいのです.








計算論的神経科学を軽く見ても全く分かりません。最低限の数式を理解するためにどの分野の数学が必要なのでしょうか?