この記事はこんな人にオススメです
- 脳波について興味がある人!
- 相関次元とは何かを知りたい人!
- 実際にプログラムを回して解析がしたい人!
こんにちは.けんゆーです(@kenyu0501_)
生体信号の一つである脳波(縦軸:振動振幅,横軸:時間)の解析をする場合,いろんなオプションがあると思います.
周波数解析(FFT)なんかは最も始めに試される信号処理ツールですが,そのような線形な解析手法を脳波に適用する場合は,もしかしたら本当に解析したいものが見えないかもしれません.
脳波のカオス的挙動をどう扱うか?
脳波を含め全ての生体信号は非線形的挙動をします.
すなわち,カオス的に振る舞うということです.
このカオス的に振る舞う性質を持つ脳波の解析をする場合には,非線形的な解析手法で問題を解くことが求められます.
(FFTなどの線形解析では過去の再現は容易にできるという特徴がありますが,どのくらい現象が複雑であるかの定量化ができないので未来の予測ができません.)
そこで今回の記事では,非線形性解析でよく使われる相関次元を用いて脳波の解析を行います.
脳波の時系列データからある規則に従った秩序を見出すことを狙いたいですが,ここでは相関次元の導出だけします.
相関次元とは
フラクタル次元の尺度を図る解析ツールの一つとして相関次元を調べるやり方があります.
相関次元とは,あるベクトルXiを中心として,その周辺の他ベクトルXjが存在する確率piを積分で解いたものです.つまり絵で描くと...(カキカキカキ)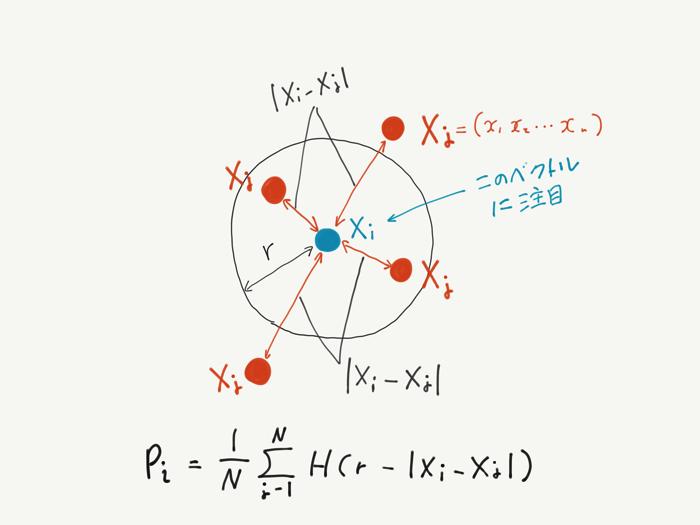
こんな感じです.注意したいことは,式中のHはヘビサイト関数といって,
H( r – |Xi – Xj| ) = 0 , r – |Xi – Xj| < 0
H( r – |Xi – Xj| ) = 1 , r – |Xi – Xj| >= 0
という決まりがあります.
あるベクトルXiというのは,時系列の連続時間データx(t)とそれを一定の時間遅れτでシストさせたずれた信号を含むデータセット群になります.
![]()
このデータセット群を用いて時系列データの軌道を再構成します.埋め込み次元mが十分に大きければ,本来のアトラクタの構造と本質的に同じ性質を持ちます.
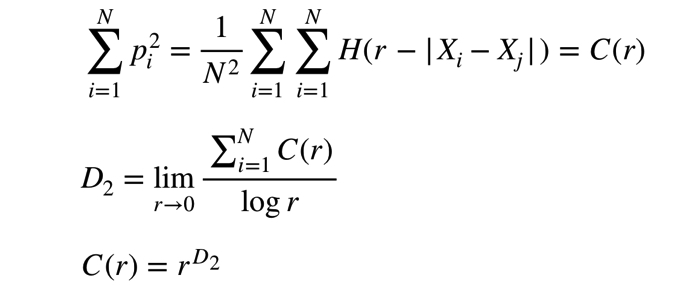
ここで相関次元D2は,この確率piに対して,
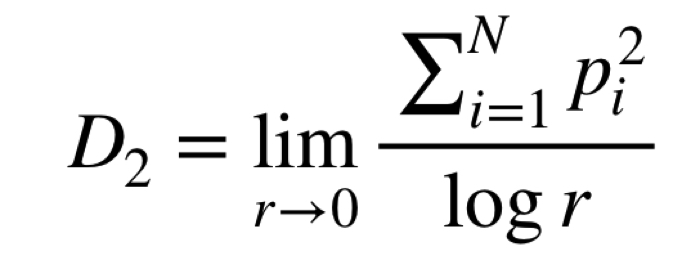
で定義されています.ここで,この相関次元D2を求めるために式変形をしますすなわち,相関次元を計算したい場合,rの変化に対するC(r)の値を算出し,得られた値を両対数のグラフへプロットし,その傾きを求めます.傾きは相関次元D2を表します.今回の記事ではこの相関次元を求めていきます.
脳波解析を実際にやってみる
ここでは相関次元を実際に脳波データに適用していきます.
使用する脳波データ:リラックス時とストレス時の脳波データ
リラックス時:ぼーっと風景画を観察している.
ストレス時:100マス計算を解いている.
どちらもアルファ波(8-13 Hz)の帯域制限を掛けた脳波です.ちなみに後頭部の視覚野という箇所のデータを取得しました.
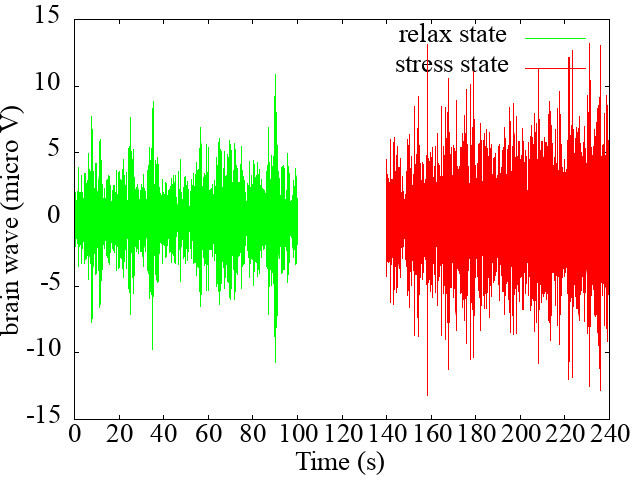
0秒 – 100秒まで → リラックス(緑)
140秒 – 240秒まで → ストレス(赤)
C言語プログラミング
井上純一先生のカオス・フラクタル講義ノートを参考に扱いやすいように組みました.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 | #define _CRT_SECURE_NO_WARNINGS 0 #include <stdio.h> #include <math.h> #define N 50000 double x[N]; double t[N]; double step( double x){ if(x>=0.0) { return (1.0); }else{ return (0.0); } } double g1[N]; double g2[N]; double g3[N]; double distance(int i, int j){ return (fabs(g1[i]-g1[j])+fabs(g2[i]-g2[j])+fabs(g3[i]-g3[j])); } double count(double epsilon, int n){ double sum; for(int i=0 ; i<n ; i++){ sum=0.0; for(int j=0 ; j<n ; j++){ sum = sum + step(epsilon - distance(i,j)); } } return ((double)sum/(n*n)); } double arg1 = 0.0; double arg2 = 0.0; double sim[N]; int main(void){ int window = 1500; FILE *input_exp; if ((input_exp = fopen("EEGdata.txt","r")) == NULL){ printf("Can't read your file 1\n"); } for(int i=0; i<N; i++){ fscanf(input_exp," %lf\t %lf\n ",&t[i],&x[i]); } fclose(input_exp); FILE *output; if((output = fopen("cd_relax.txt","w")) == NULL){ printf("Can't make new file 2\n"); } for(int k=0 ; k<N-1000 ; k++){ g1[k] = x[k]; g2[k] = x[k+10]; g3[k] = x[k+20]; } for(double epsilon = 1.0 ; epsilon < 20.0; epsilon = epsilon+0.1){ arg1 = count(epsilon, window); arg2 = epsilon; printf("%.3lf\t %.3lf\n",log(arg2), log(arg1)); fprintf(output,"%.3lf\t %.3lf\n",log(arg2), log(arg1)); } fclose(output); } |
ちなみに相関次元の各種条件設定はこちら!
- 時間遅れ τ = 0.02 sec
- 埋め込み次元 m = 3
- データ点数 1500点 (3秒分)
解析結果
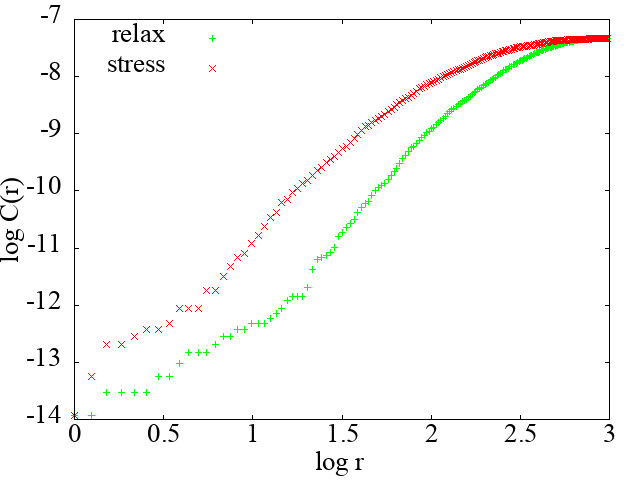
このような解析結果になります.相関次元は,log rとlog C(r)の傾きですので,だいたいリラックス時の脳波が4程度,ストレス時の脳波が3程度になりました.
この解析で得られた信憑性を確認してみます.以下は合原一幸先生が書いた「ニューラルシステムにおけるカオス(東京電機大学出版局)」の脳波の相関次元解析の一例です.
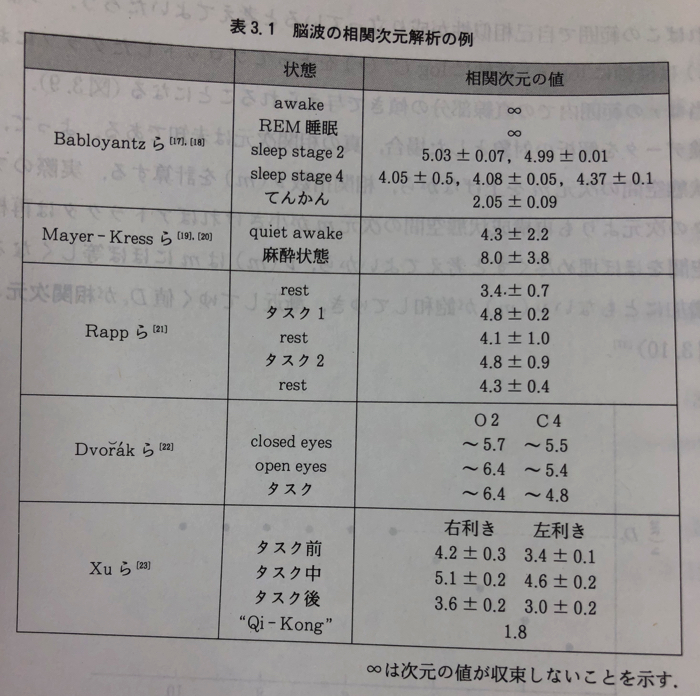
こちらの書籍によると,相関次元の値が4程度なら大体良い感じですね!
考察とまとめ
今回のちょびっと解析した結果によると,脳波の相関係数はおおよそ3〜4をとったので脳波の時系列波形の特徴を説明するためには,少なくとも3〜4程度の自由度を持つモデリングが必要な事がわかりました!
でもこの自由度って具体的にみるためには凄く難しんですよねー.
だって4次元とか5次元のマップって作成するのほとんど無理ですもん.
3軸+カラーリング+プロットの大きさとかを使えばギリ可能かと思いますが,そこはもはやアートの域に行きます笑
脳波の研究は奥が深いのです.
ちなみに今回参照した参考書はこちら!