- Duffing(非線形)振動子について知りたい人
- 数値解法プログラム(オイラー法)について知りたい人
- カオス的な挙動について興味がある人
おいらの研究では脳波の挙動をDuffin振動子(もしくはダフィング振動子)という簡単な一自由度の非線形振動子(運動方程式)でモデリングをしてます.
このような感じです.
今回は,そんなDuffing振動子について色々と情報をシェアして,その後簡単な数値解法プログラムを構築して,挙動を確認していきたいと思います!
Duffing振動子についての基本的な理解
Duffing振動子の基本的な理解は,すでに多くの知的ブロガー様たちが解説してらっしゃるので,勝手にオススメしておきます.
- Wikipedia
→一通り書かれてます.とっかかりはこれ! - Duffing振動子のカオス的運動シミュレーション
→時系列シミュレーションとそのプログラムが紹介されていて凄く勉強になります.超絶おすすめ! - Pythonでカオス・フラクタルを見よう!
→Duffing振動子の挙動だけではなく,フラクタルについてのプログラムもあるので参考になりますよ! - カオス&非線形力学入門
→超豊富なアニメーションが見れます.製作者の金丸先生には脱帽です.これは有料で良いレベルだと思います.超絶オススメ!
脳波モデルとして使用するDuffing振動子のシミュレーション
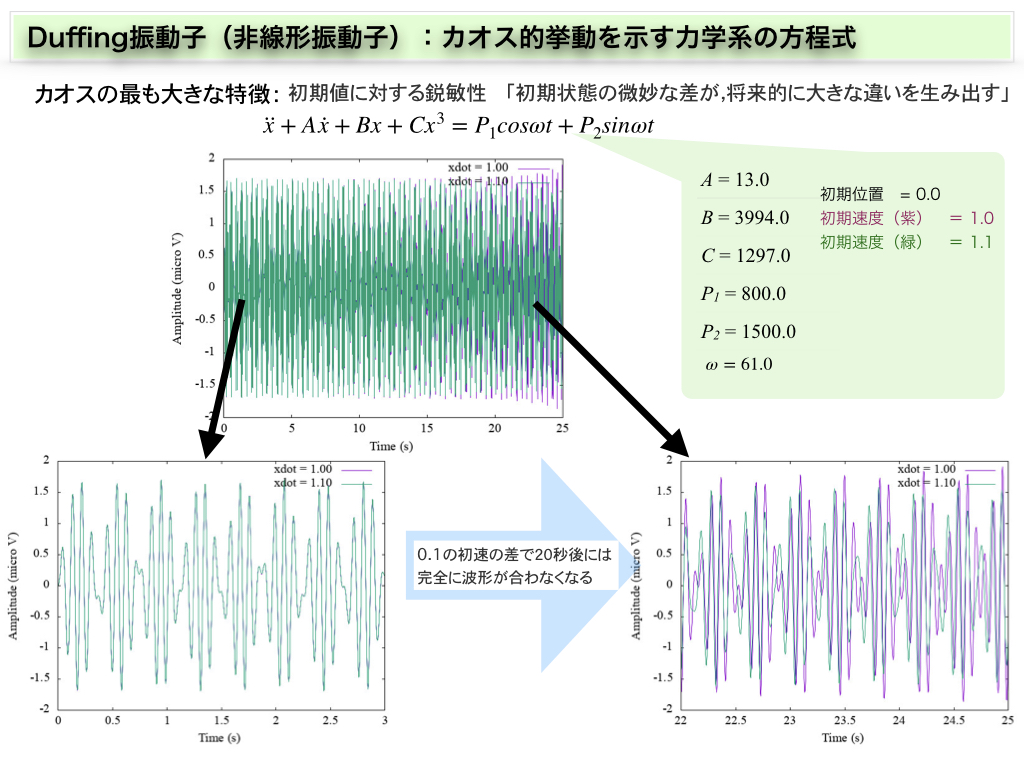
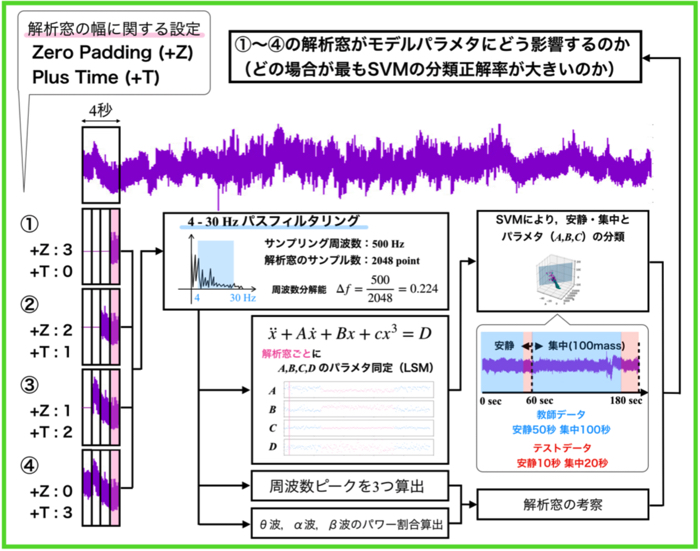
おいらの研究の場合は,Duffing振動子に内包する特性パラメータ(ばね定数やダンピング定数,非線形定数など)は実験的に調べます.
カオス的な振る舞いとは”初期値に依存して未来の挙動が大きく変動する”という特性を持つのでそういった挙動が観察できれば良いかと思います.(上のスライド)
解析プログラミング
以下に解析プログラミング(C言語)を示します.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 | #define _CRT_SECURE_NO_WARNINGS 0 #include <stdio.h> #include <math.h> #include <stdlib.h> #define N 50000 #define Window 12500 #define P 100 #define dt 0.002 FILE *out; double A; double B; double C; double P_cos; double P_sin; double w; double xdotdot[Window+2]; double xdot[Window+2]; double x[Window+2]; double x2dotdot[Window+2]; double x2dot[Window+2]; double x2[Window+2]; double t; FILE *gplot; char *out_data; int main(void){ A = 13.0; B = 3994.0; C = 1297.0; P_cos = 800.0; P_sin = 1500.0; w = 61.0; out_data = "duffing.txt"; out = fopen(out_data,"w"); //gnuplot gplot = popen("gnuplot -persist","w"); fprintf(gplot,"set yrang[-2.0:2.0]\n"); fprintf(gplot,"set xrange[0:25]\n"); fprintf(gplot,"set xlabel \"Time (s)\"\n"); fprintf(gplot,"set ylabel \"Amplitude (micro V)\"\n"); fprintf(gplot,"set xlabel font\"Times New Roman,15\"\n"); fprintf(gplot,"set ylabel font \"Times New Roman,15\"\n"); fprintf(gplot,"set key font \"Times New Roman,15\"\n"); fprintf(gplot,"set tics font \"Times New Roman,15\"\n"); x[0] = 0.0; xdot[0] = 1.0; x2[0] = 0.0; x2dot[0] = 1.1; for(int i=0; i<Window ; i++){ t = i*dt; xdotdot[i] = - A*xdot[i] - B*x[i] - C*x[i]*x[i]*x[i] + P_cos*cos(w*t)+ P_sin*sin(w*t); x2dotdot[i] = - A*x2dot[i] - B*x2[i] - C*x2[i]*x2[i]*x2[i] + P_cos*cos(w*t)+ P_sin*sin(w*t); xdot[i+1] = xdot[i] +xdotdot[i]*dt; x2dot[i+1] = x2dot[i] +x2dotdot[i]*dt; x[i+1] = x[i] + xdot[i]*dt; x2[i+1] = x2[i] + x2dot[i]*dt; fprintf(out,"%.3lf\t %.3lf\t %.3lf\n ",t,x[i],x2[i]); //fprintf(gplot,"%.3lf\t %.3lf\t %.3lf\n",t,x[i],x2[i]); } fprintf(gplot,"plot \"%s\" using 1:2 with lines t \"xdot = %.2lf\", \"%s\" using 1:3 with line t \"xdot = %.2lf\"\n ",out_data,xdot[0],out_data,x2dot[0]); fclose(out); fprintf(gplot,"set term jpeg\n"); fprintf(gplot,"set out \"duffing_2.jpg\"\n"); fprintf(gplot,"replot\n"); fprintf(gplot,"set term aqua\n"); fclose(gplot); } |
今回は,初期値依存のカオス的な挙動を確認したいために,二つの軌跡(xとx2)をオイラー法により同時に求めました.
サンプリングタイムdtは0.002秒です.
ルンゲクッタ法を使えばもう少しサンプリングを広く設定しても良いかもしれません.
オイラー法は一次近似なのでサンプリングタイムをどうしてみ短くしないと精度が担保できません.
プログラミングはMacのターミナルから直接コンパイルを実行しており,C言語上でgnuplotを呼び出しグラフを記述してます.
(popen関数でgnuplotを使うためのパイプを構築してます)
なので,macを使用していてgnuplotを入れている方は実行するとこの記事と同じグラフが作成されると思いますので試して見てください.
1 2 3 | kenyu-MacBook-puro:2018.8.29_duffing (^^)$ c++ duffing.cpp -o duffing.out kenyu-MacBook-puro:2018.8.29_duffing (^^)$ ./duffing.out |
ターミナル上でプログラムテキスト(.cpp)のあるディレクトリでコマンドを実行して見てください.
このような図が出てくると思います.
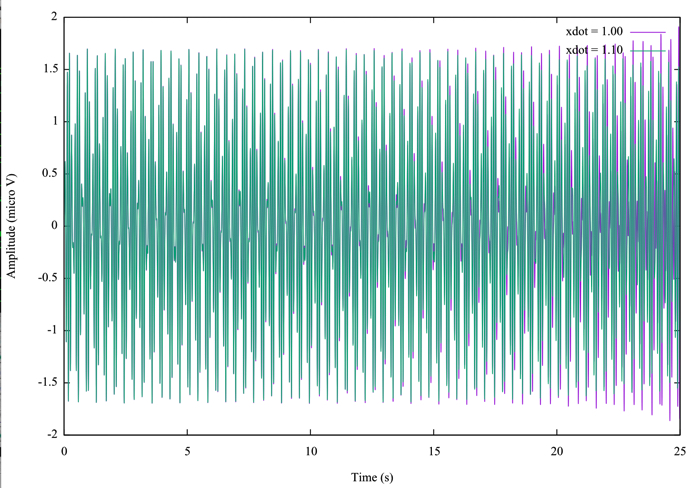
ちょっとした観察
Duffing振動子の動きはカオス的なので,初期値のちょっとした違い(今回は初速度)が後の時間波形にものすごく影響して挙動が変化するといった動きを見せます.
これは,カオス性という事ですが,脳波の動きとか,脈波だとか生体の循環システムなどはカオス的に動いているとされているので,もそ興味があれば皆さんもDuffing振動子で生体信号のモデル化をやってみても良いかもしれませんね!
以下はこの分野に必読&おすすめの2冊です
ストロガッツの非線形ダイナミクスとカオスと,非線形力学とカオスです.