- 脳波界隈の研究をしている人
- 生体医工学に興味がある人
- 集中度合いの可視化が気になる人
こんにちは.
2018年10月27日に松江医療センターで開催された日本生体医工学会 中国四国支部に参加してきました.
発表タイトルは「ゆらぐヒト脳波データからどのように集中度合いを可視化するか」です.
学会の発表件数が少ないであろうと予想し,おそらく脳波界隈の研究者はあまり来ないだろうと考えて,タイトルに専門用語を使わないようにしました.
資料を作成したので以下に発表で使ったスライドをまとめておきます.
脳波を用いた集中度合い:リアルタイムFFT
脳波とは
脳波とは!?
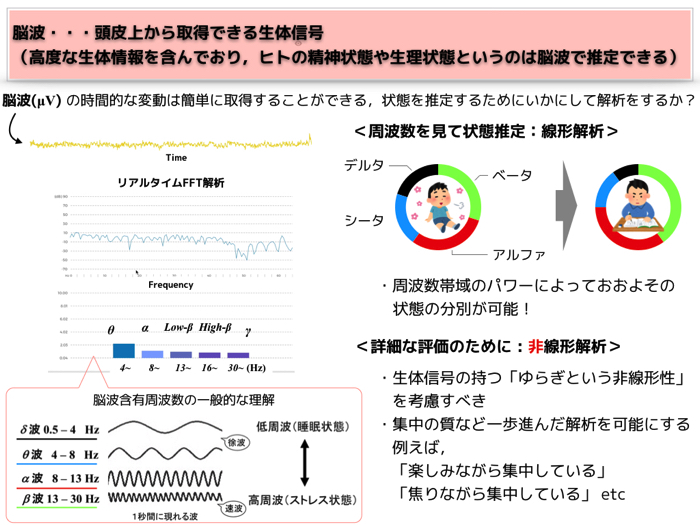
今回扱うのは,頭皮上から取得できる脳波(EEG)を使用しています.
脳波は生体信号の中でも最も高度な情報を持っているので,解析をすることによって状態推定を可能とします.
簡単に時間的変動を取得することができますが,どのようにして解析をするのかが大きなポイントです.
リアルタイムFFT(周波数解析)
脳波に含まれる周波数成分を見ると,とても簡単に集中度合いを把握することができます.
1秒間に約10回程度振動するアルファ波を基準として,それよりも速い波をベータ波(13 – 30 Hz)がより多く含まれていると割とストレスフルであり,アルファ波よりも遅い波であるシータ波(4 – 8 Hz)およびデルタ波(0.5 – 4Hz)がより多く現れていると眠たい(もしくは睡眠)状態だったりします.
まあ,一般的に集中状態が高くなると,脳波の時系列データに含まれる高周波成分の周波数の含有率が大きくなるわけですね.
周波数の成分を見ると,個人差を考慮してはいませんが,おおよそストレス状態を評価できると言われています.
しかしながら,周波数解析のようなある種単純な足し合わせの原理で成り立つ線形解析では,やっぱり集中度合いの詳細な評価はできないと思います.
脳波はゆらぎますもんね!
脳波のカオスという性質に注目する
脳波の性質は?
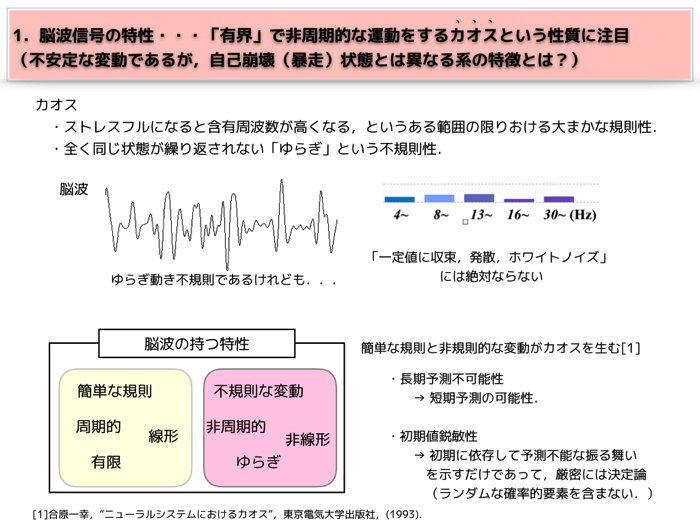
脳波の振る舞いは非常に複雑です.
しかしながら,ある電位の範囲で変動しますし,ある周波数の範囲を持って振動します.
集中状態になるとベータ波やアルファ波が増えるという「簡単な規則」もあります.
また,生きている限り,脳電位は一定値に収束することはないですし,爆発的な発散(てんかん性異常脳波は除く笑)もない,またホワイトノイズ的なランダム性もない.
でも細かい変動は,やっぱり揺らいでいるので同じ状態になるというのは全くありません.とても不規則な変動をします.
つまり,脳波は「簡単な規則的な動き」と「複雑な不規則な変動」を合わせ持っているのです.
脳波のモデリングと解析方法

モデリングについて
脳波の挙動自体は,確率的要素,すなわちランダム性が無いので決定論的に振る舞うと考えています.
決定論的というのは,数学的に記述できるということです.
例えばニュートン力学系の方程式,ボールの放物線軌道などは,完全に決定論的的です.
おいらの研究では,Duffing振動子という一自由度のモデリングをしてます.
機械系の学生は,大学の授業で習うと思いますが,「粘性減衰振動系」の線形振動子に,Cxの3乗の非線形項がついた簡単な式です.
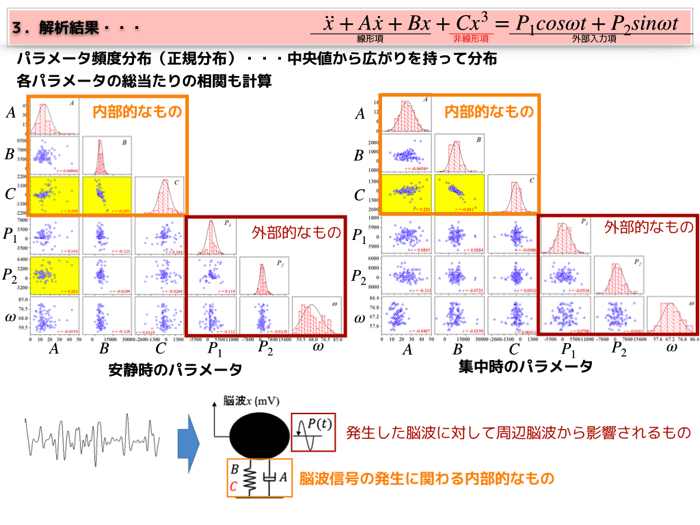
左辺は,取得した脳波信号の発生に関わる内部的なことを想定します.
右辺は,周辺脳波からの影響を受けていると想定し,三角関数の周期加振で表現してます.
脳波解析について

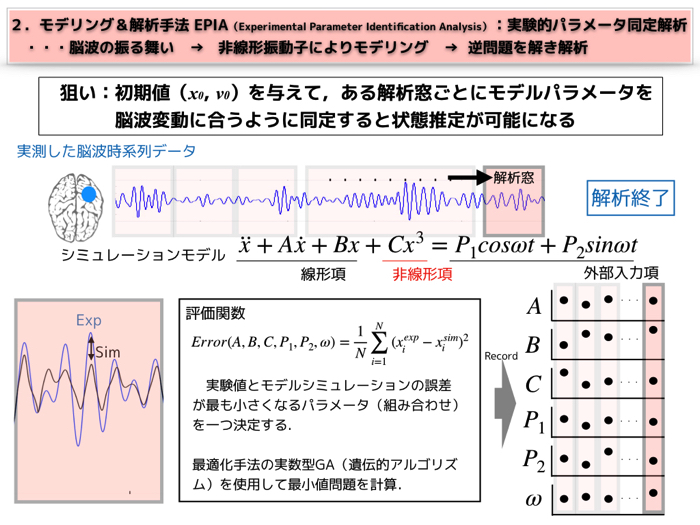
このような形で,実測値脳波に合うようなモデルパラメータ値を時事刻々定めて行きます.
評価関数を最小とする際のモデルパラメータの組み合わせを実数型遺伝的アルゴリズムによって定めました.
またいつかプログラムの公開をします笑
定めたモデルパラメータを確認して,集中度の確認をしていくというのが本研究です.
実験に関して
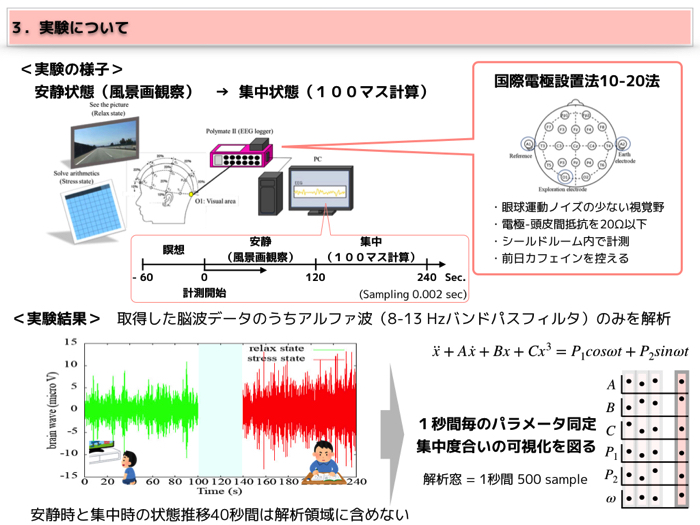
実験は以上のように行いました.
安静時脳波と,集中時の脳波を100秒間取得します.
できるだけノイズを入れたくないので,実験はシールドルームで実施しました.
脳波の取得位置は,後頭部(視覚野)です.
前頭葉で所得すると,瞬きによる生体ノイズが混入するので後頭部にしました.
さらに前日のカフェイン制限をしてます.
解析結果
エラー値とシミュレーションの精度について
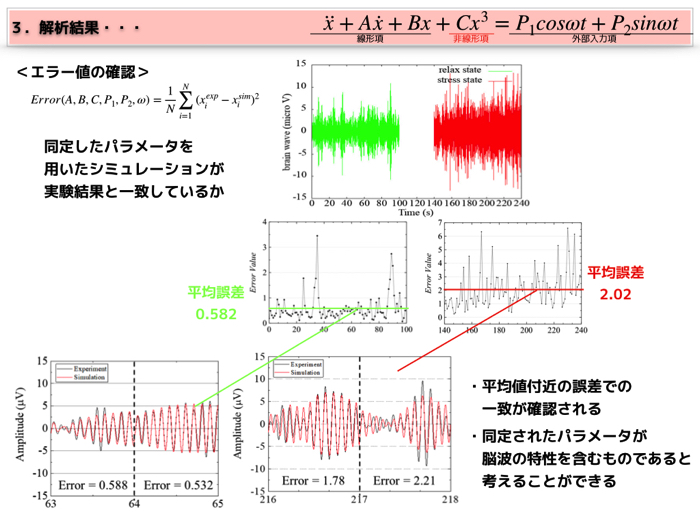
100秒の解析において,1秒窓で解析をしたので,エラー値の値も100点計算されます.
安静時と集中時で平均値が定まり(それぞれ0.582と2.02),その平均値付近のシミュレーション結果と実験結果を確認するとほとんどの一致が確認されました.
すなわち,脳波の振る舞いは決定論的にやっぱり書くことができて,単純な一自由度な方程式でモデリングすることができるのですね.
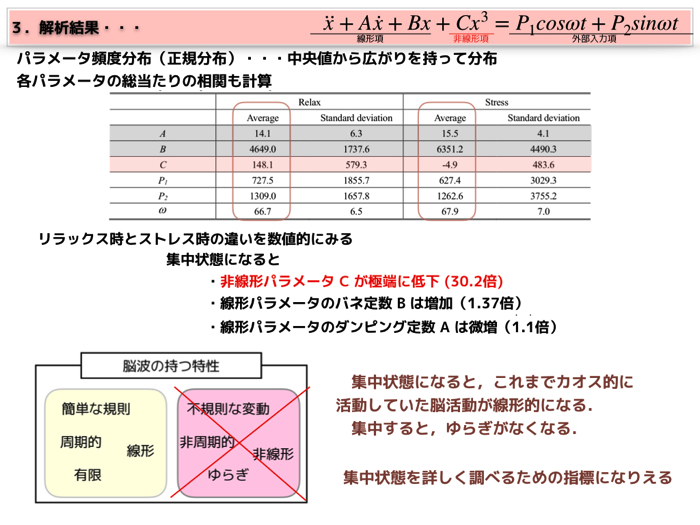
モデルパラメータの結果は!?
あとは,スライドを貼っておきます.
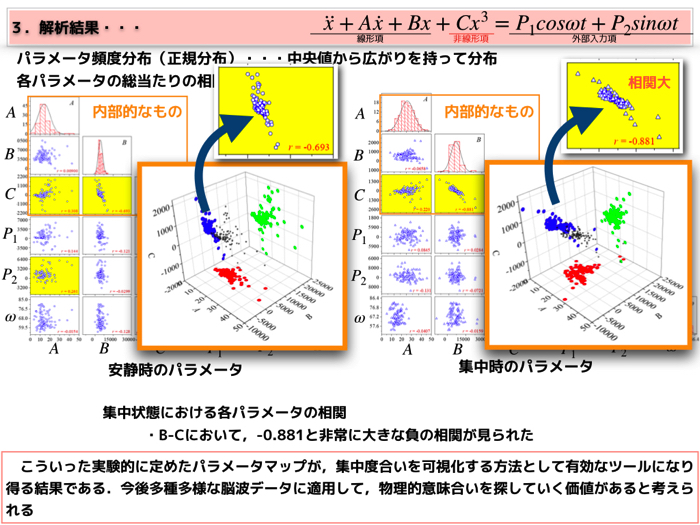
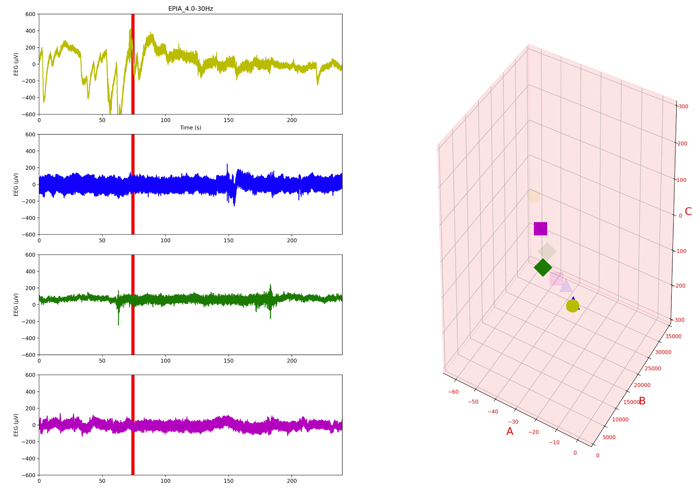
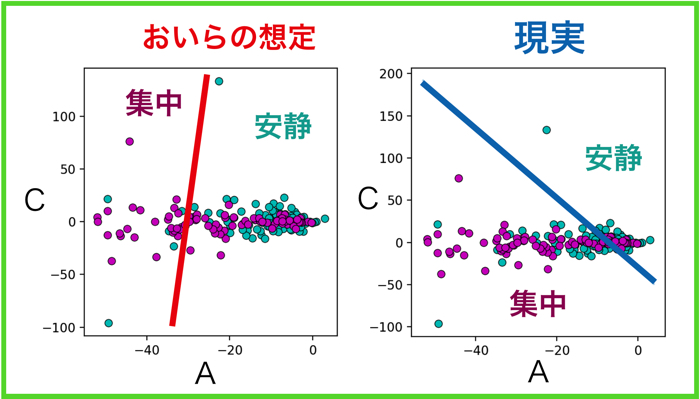
最終的に集中度合いをどのように見るのかというのは,モデルパラメータの分布で確認することになります.
最後のスライドのモデルパラメタA,B,Cの値を見ると集中度合いがどのようになっているのか確認することができます,