- 最適化手法に興味がある人
- パラメータ同定(推定)をしている人
- 評価関数を意識せずに使用している人
こんにちは.けんゆーです(@kenyu0501_).
今日は,最適化問題とかでよくパラメータを決める際にカギとなる評価関数のお話をします.
「評価関数」はいろんな呼ばれ方があって,例えば「目的関数」とか,「Error関数」,「エラー関数」とか,「誤差関数」とか,「成績関数」とか...
結論から言うと,全部一緒だと考えていいと思います.
言葉とか数式を使う側の好みの問題だと思っていいです.
大事なのは,その評価関数がどのような内部構造をしているか!と言うことです.
評価関数はどういった状況で使うのか?
色々とありますが,代表的なものでいうと逆問題を解く場合ですね.
すなわち,実験的にモデルの内側のパラメータを推定する場合です.
今日はとりあえずテーマとして,モデルパラメータを決める際に,
「実験値の誤差を直接下げれるような値を決めるには!?」
と言うことで話を進めていきたいと思います.
ちょっとスライドを用意してみました.

だいたい上のスライドを見てもらうと,理解しやすいのではと思いますが,評価関数の種類として使われる種類として以下の3つの式があります.
(誤差とは,実験値のモデルシミュレーションの値の誤差です)
- 絶対誤差
- 二乗誤差
- 相対誤差
この誤差を最小にするようなモデルシミュレーションを行えるパラメータを同定したい!と言うわけです.
それぞれの評価関数にはそれぞれ特性があるので,一つ一つ見ていきましょう.
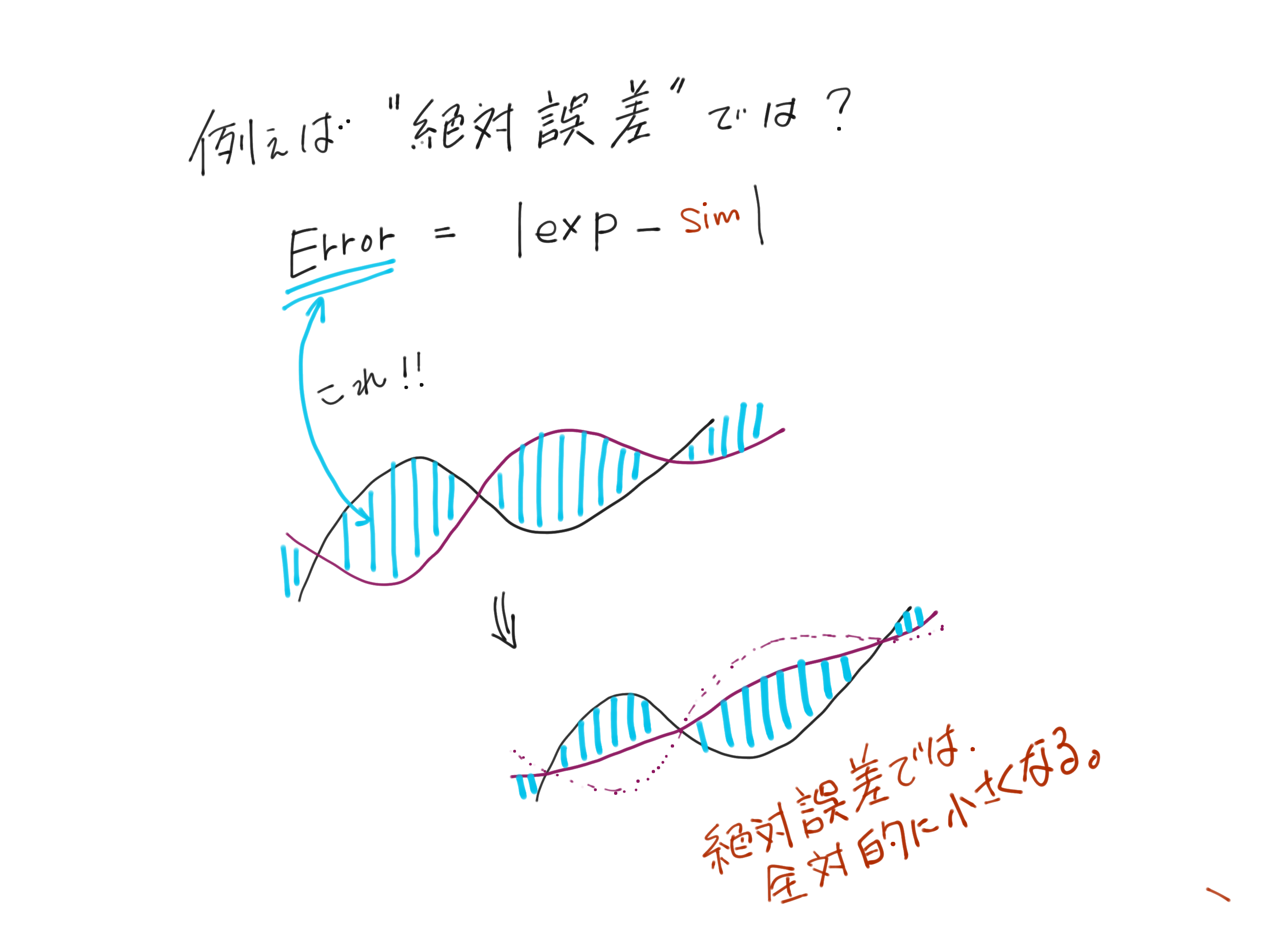
絶対誤差は!?
絵を描きました.
絶対誤差は,実験値との単純な誤差なのでこんな感じです.
緩やかな実験値に対しては効果をものすごく発揮します.
ただ,振動系モデルのパラメータ推定には非常に弱いです.
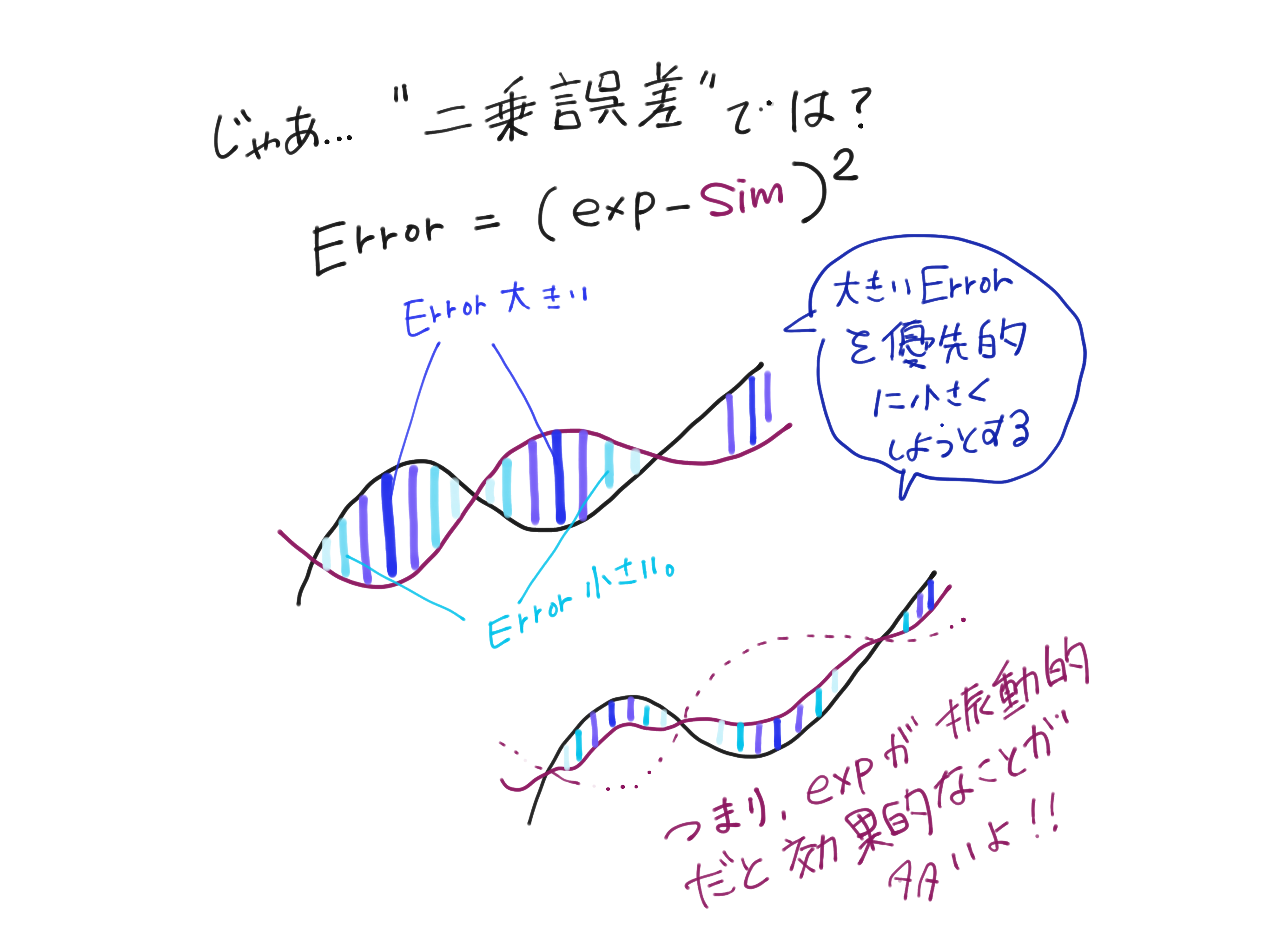
二乗誤差は!?
大体の評価関数を見たら使われているものですよね.
二乗されているので,実験値とシミュレーション値の直接的な差(誤差)が1を超えると途端に誤差が大きくなります!
つまり,直接誤差が例えば2の時,二乗すると,2×2=4で大きくなります.
(逆に直接的な差が1以下であれば,小さく出力されます.例えば,直接誤差が0.1の場合,0.1×0.1=0.01で小さくなる!)
なので,評価関数を小さくするためには,より大きな誤差を小さくしたほうが,式的にお得なのです.
振動系のモデルとかであれば,良いと思いますよ.
また三乗とか四乗誤差とかもワンチャンありかもしれません.
(マイナスを取る可能性が出る場合は,奇数乗は避けるか,絶対値をつけてください.)
相対誤差は!?
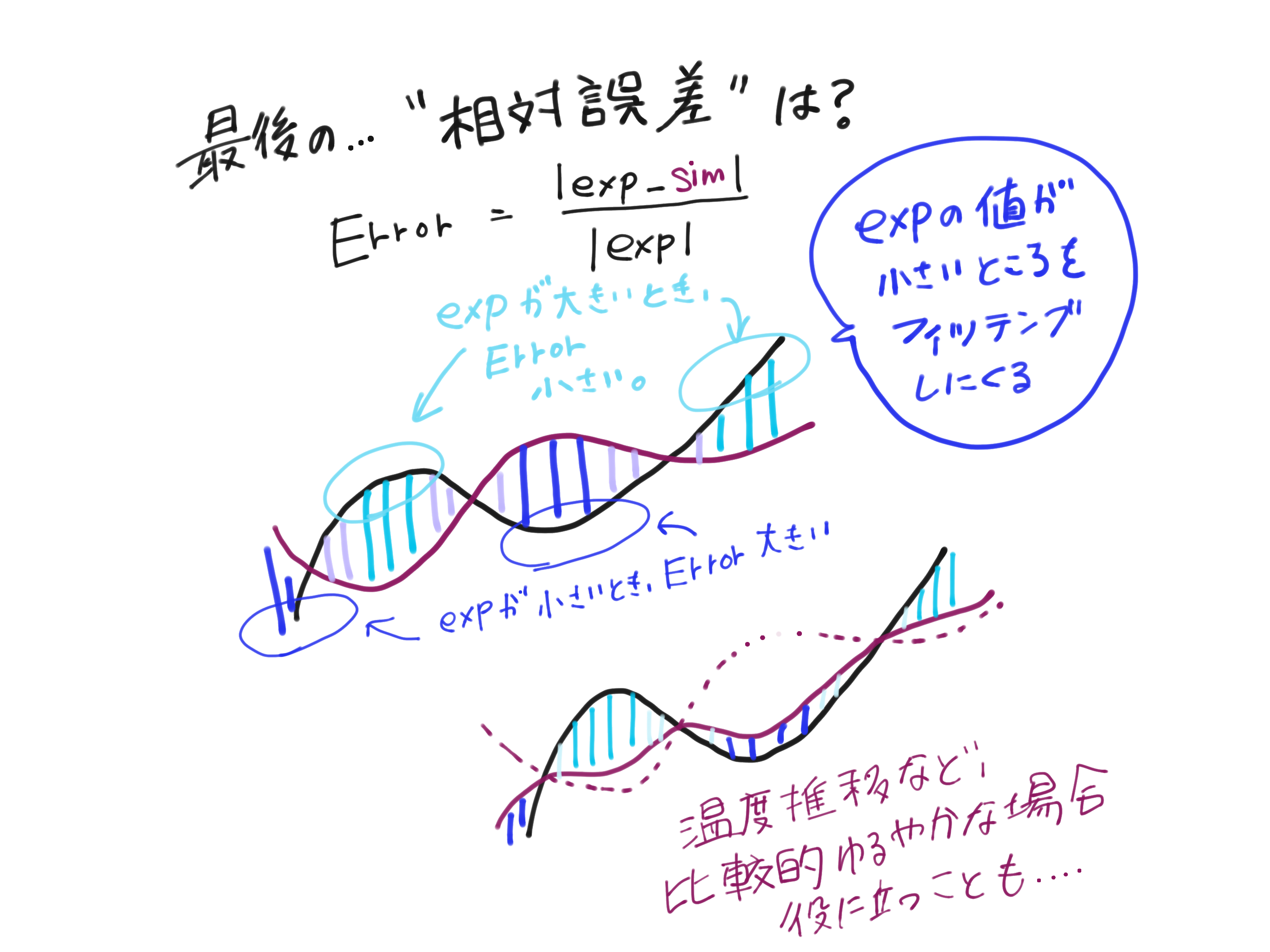
相対誤差,これは結構面白い評価関数です.
実験値の値のオーダーによって誤差が変わります.
つまり,実験値で割っているので,実験値自体の大きさが小さければ,評価関数は大きく見積もられるのです.
なので,実験値のオーダーが小さい所をより意識して合わせにいきたい!などある特定な理由がない限り使う理由がありません.
以前ペルチェ素子の温度モデルを研究していたときには使ったことがあります.
その時は,低温状態のモデルシミュレーションは上手く合いましたね笑
そんな感じです.ではー!