- 数学や工学が好きな人
- 非線形ダイナミクスが好きな人
- 分岐とかそこらへんを勉強したい人
こんにちは!分岐の話題もこの記事で3本目です.
(1.ダイナミクスのパラメータ依存性を考えて分岐を解く)
(2.亜臨界ピッチフォーク分岐からジャンプやヒステリシス性を見る)
それぞれ基本的分岐とちょっと特殊な亜臨界ピッチフォーク分岐について書きました.
どちらとも話の条件としては,1次元系 dx/dt=f(x) を扱っていて直線上xのベクトル場として見なして良いという考えを用いてきましたね!
そして,3次の項や5次の項が出てきましたが,内側の変数として取り扱うパラメータに関しては r の1つのみでした.
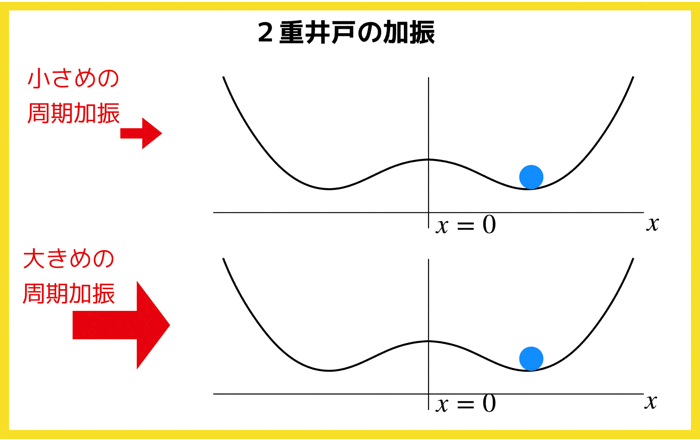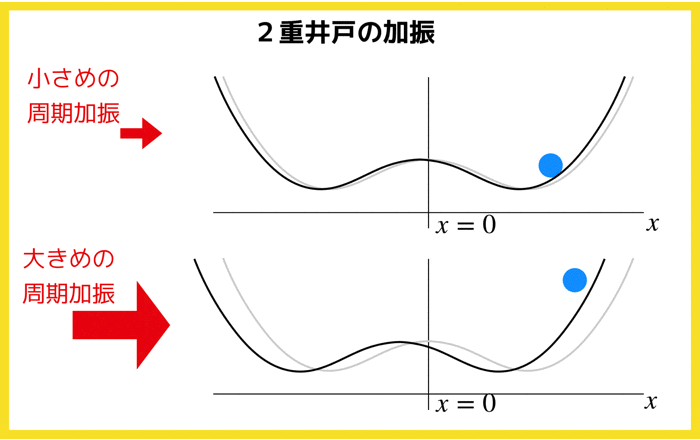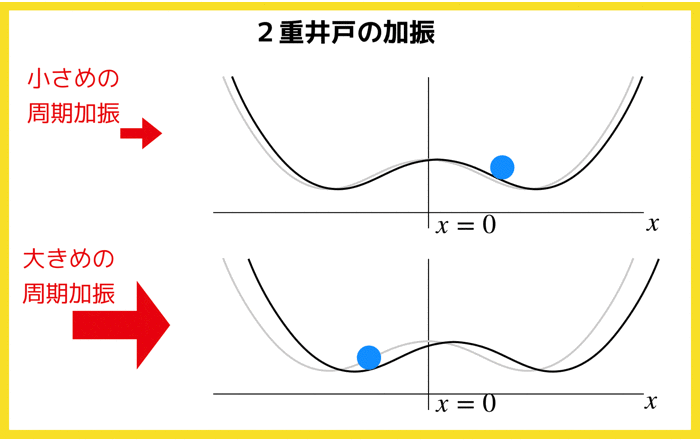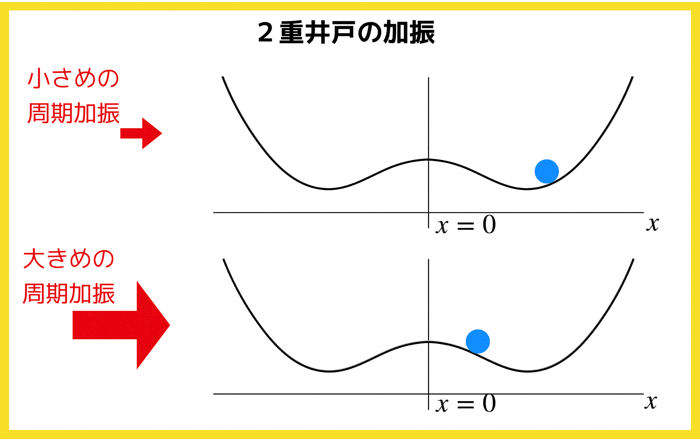
今回は,内側のパラメータを1つ増やして(でもまだ1次元系),
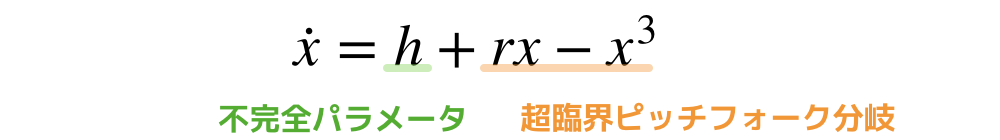
以上の形の分岐を考えていきたいと思います.
h=0 では,普通の超臨界ピッチフォーク分岐が起きますが,定数hがあるためベクトル場が全体的に上下するというイメージです.
ちなみに,このhを不完全パラメータと言います.
超臨界ピッチフォーク分岐なら,x=0に対して対称性がありましたが,hが加わることによってその対称性が崩れます.
そのため,不完全パラメータという呼ばれ方になっています.
2つの独立変数 r, h を考える
まずは,rからです.
これは,超臨界ピッチフォークなので,
- r<0の場合 → 安定固定点が1つ
- r>0の場合 → 安定固定点2つ+不安定固定点1つ
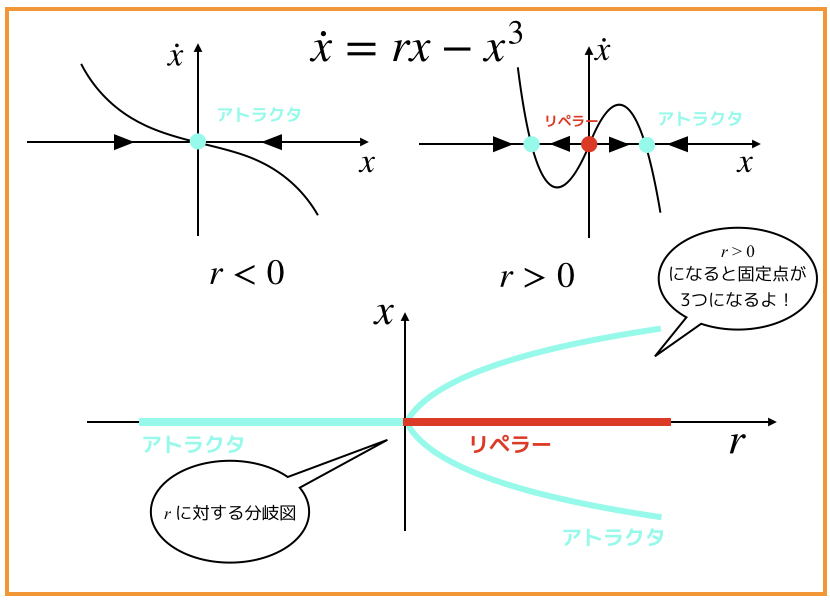
ですね.簡単な復習です.
今回は,rの他にhも変動するので,少々大変です.
とりあえず,考え方の指針として,rを一定値とした場合のhの影響について考えたい.
そこで,y=-hと,y=rx-x^3の2つのグラフの交点を求めます.
上の図で注目すべきことは,右側のr>0の時ですね.
hの値によって交点が増えます.
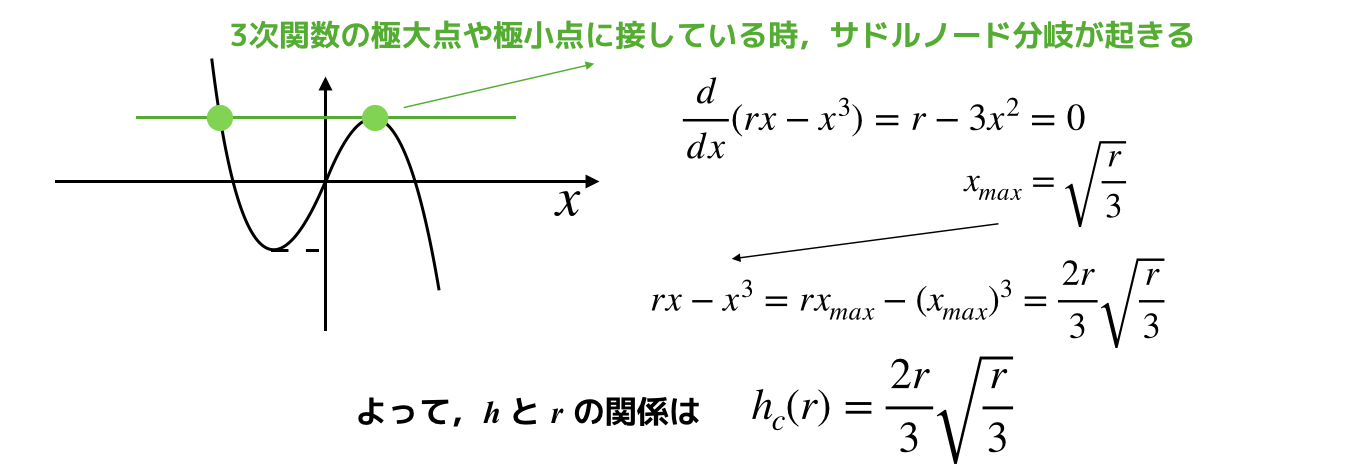
上の図は,サドルノード分岐が起きる場合のhとrの関係です.
2つの線がちょうど接する場合 hc に,サドルノード分岐(固定点が2つ)が生じるのですね.
また|h| < hc の場合は3つの固定点を持ち,|h| > hc の場合は,1つの固定点です.
これらの結果をまとめると以下のようになります.
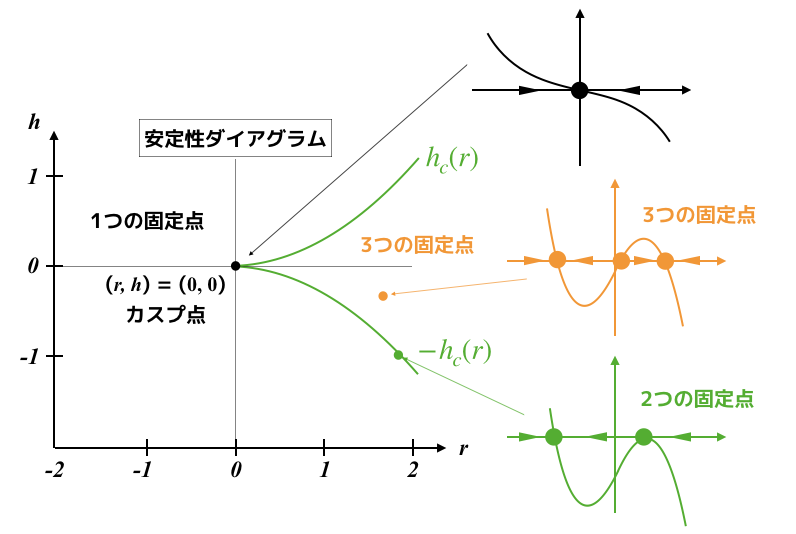
rとhのパラメータの値に対する安定性ダイアグラムです.
(0,0)の点は,カスプ点と呼ばれます.
3次元的に図示する
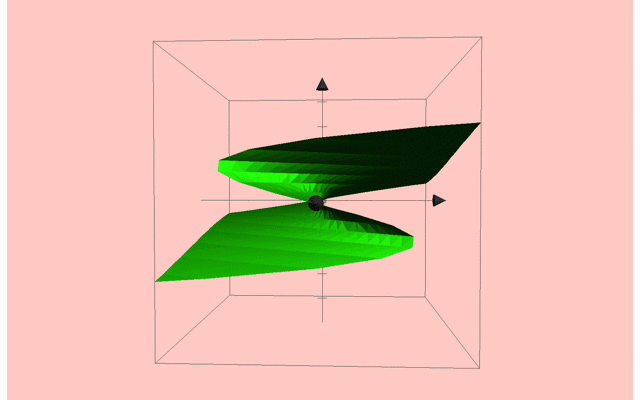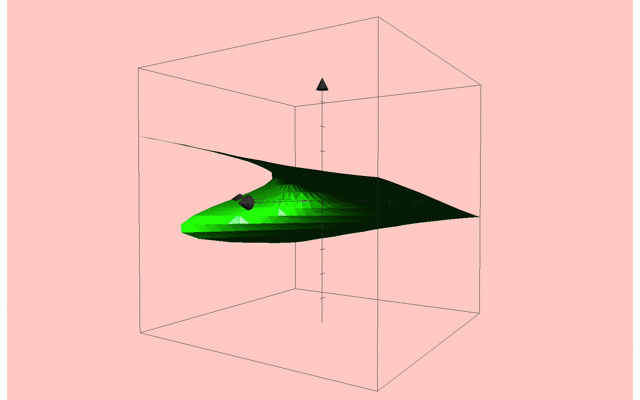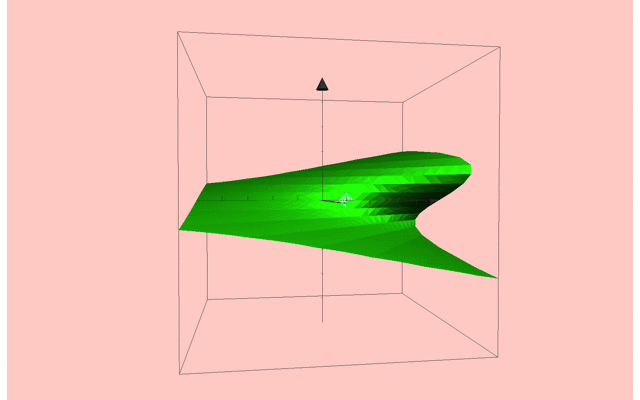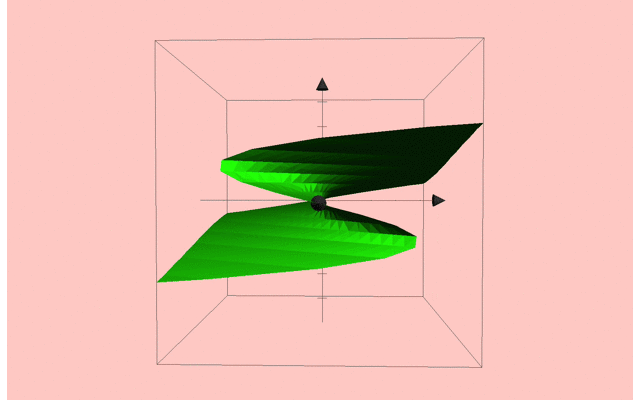
また,この (r,h)平面に対して,それぞれの固定点xを3次元的に図示して行くと,このようになります.

ちょっと頑張って図を作ってみました.
下の(r,h)平面に対して,固定点xを図示していくと,カタストロフィー面という面白い形状に遭遇します.
この局面は,ある箇所でそれ自体に折り重なるように畳み込まれてます.
パラメータの変化によっては系の状態が上側の端においやられ,下側の曲面へ不連続的に落下します.
これも一種のジャンプです.
ちなみに,以下は3Dの回転図を作ってみました.

カタストロフィーの簡単な例などは,以下「ストロガッツ 非線形ダイナミクスとカオス」が詳しいです.
昆虫の大発生や,簡単な力学系など具体例を紹介していて面白いです.