- 微分方程式が好きな人
- ダイナミクスな系が好きな人
- 振動工学を学び始めた大学生
こんにちは.以前「非線形微分方程式の解を幾何学的に算出する」という記事を書きました.
直線上(x軸)に対応するベクトル場(dx/dt)を観察することで,系の解を導出するという方法でしたが,この記事では,それのちょっと進化版で円周上の流れについて考えていきます.
円周上の点θ
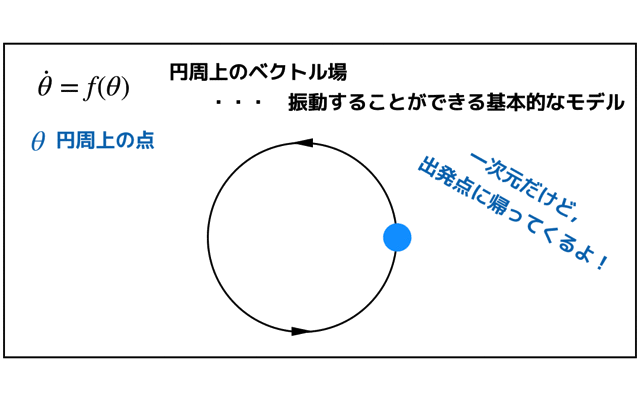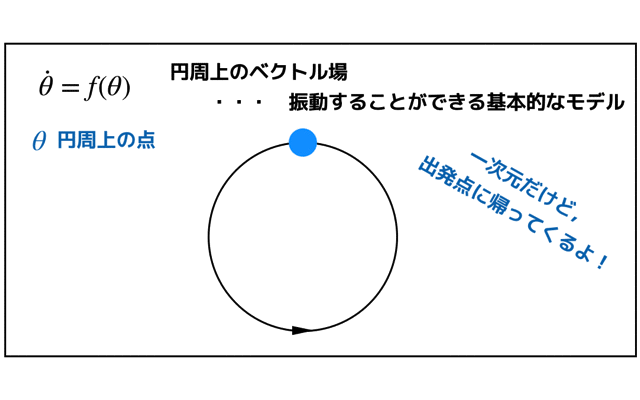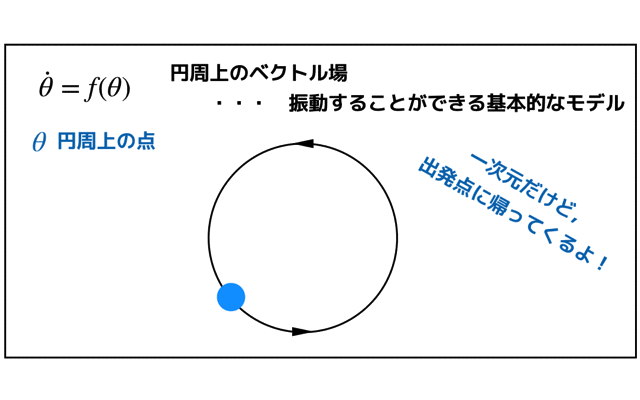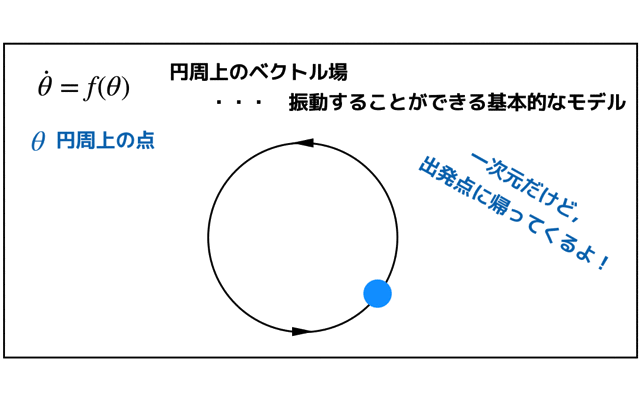
扱うベクトル場は以下のような円周上です.円周上の点はθになります.

一次元系ですが,一方向に流れていき出発点に戻ってくるので,振動を表すことができる基本的なモデルになります.
(周期解が出てくるよ!)
この基本的な系を学べば,ホタルの周期的な発光や超伝導ジョセフソン接合素子の電圧の振動などが理解できるかもしれません.
(詳しくは,ストロガッツ 非線形ダイナミクスとカオスへ)
sinθのベクトル場を考える
上の本書からの問題文を引用しますが,このブログでも以下の式をはじめに考えていきます.
![]()
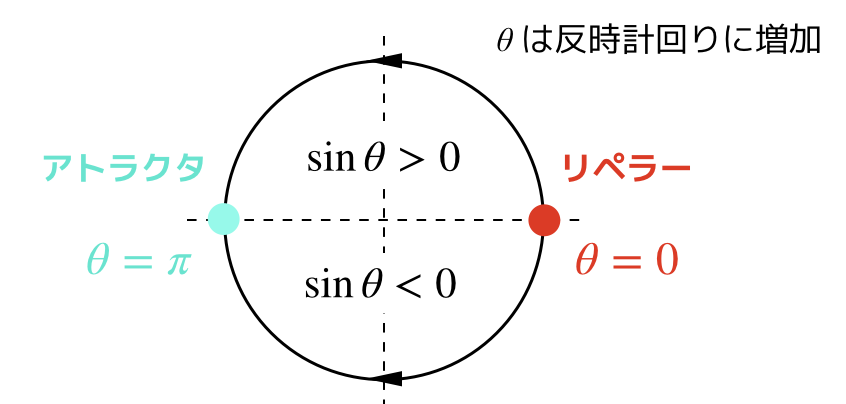
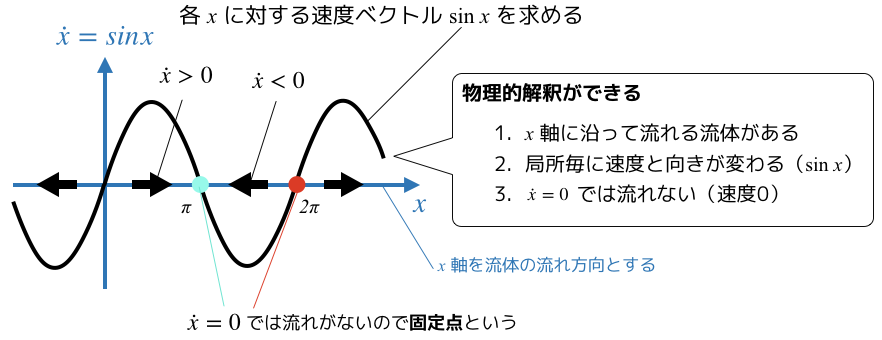
前回の記事でやったdx/dt=sinxは直線上のベクトル場を考えたが,今回は円周のベクトル場なのです.
前回の記事はこちら「非線形微分方程式の解を幾何学的に導出する」.
なお,今回の円周上のベクトル場においては,-∞<θ<∞ の範囲で考えることはできません.
これは,θ=0と2πは,位置的に同じであるが,速度(dθ/dt)は異なるからです.
ということで,この非一意性を避けるために,-π<θ<π の範囲で限定することにします.
つまり,円周上のベクトル場のルールは,円周上の各点θに一意的に速度ベクトルを当てはめることで行う.
非一様な振動子を考える
以下の方程式を考えていきます.
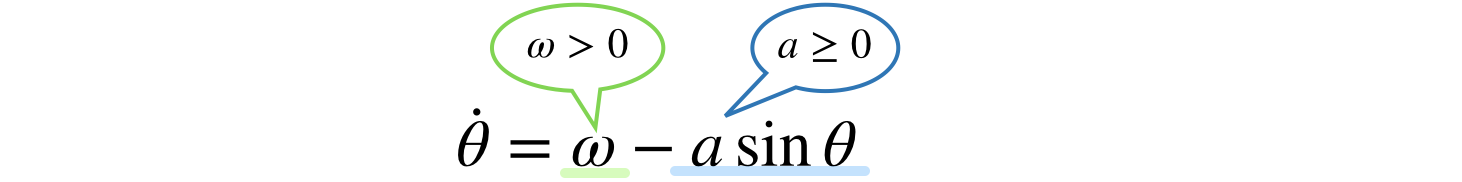
内側の各パラメータωとaに関しては,簡単のために正ということにしておきましょう.
ベクトル場の確認
aが0の場合
速度が一様な振動子になりますが,aが入ることによって速度に非一様性が生まれます.
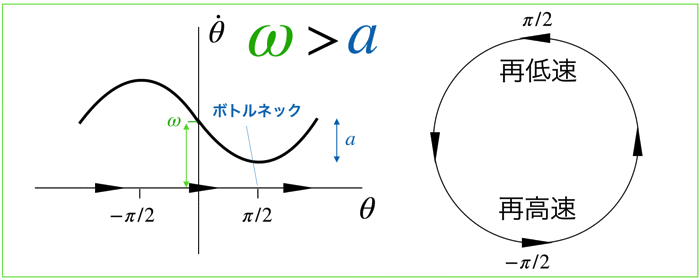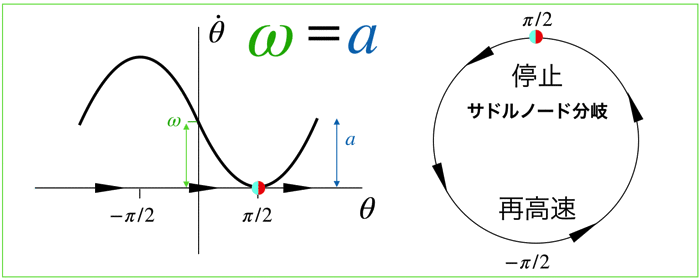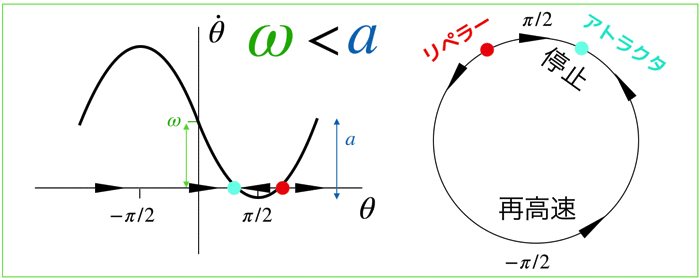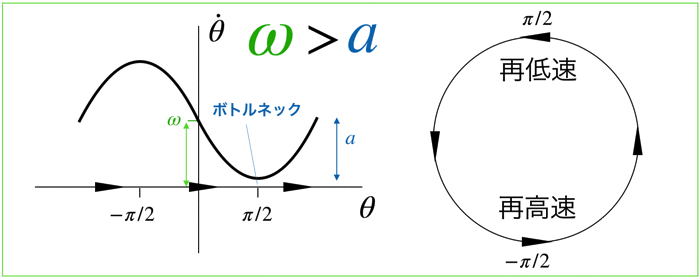
ω>aの場合
ベクトル場を見たら確認する頃ができますが,速度は θ=-π/2 でもっとも速いです.
逆に θ=π/2 でもっとも遅くなります.
この速度の非一様性は,aの値が大きくなればなるほど顕著になります.
θ=π/2 では最も遅くなるため,相空間の点θは,π/2を通過するためにものすごく時間がかかます.
(ボトルネックと言います)
この点を通過すると徐々に速度を増していきます.
ω=aの場合
系は振動しません.サドルノード分岐によって,系は半安定な固定点にいきます.
(サドルノード分岐について知りたい人はこちら「ダイナミクスのパラメータ依存性を考えて分岐を紐解く」)
ω<aの場合
アトラクタ(安定固定点)とリペラー(不安定固定点)が現れます.
t → ∞ で安定固定点に引き込まれます.
ボトルネックに費やされる時間
ω>aの場合
速度は θ=π/2 でもっとも遅かったですね.このとき,この点θを通過するときにものすごい時間がかかることをボトルネックと言いました.
実際に固定点はないですが,この付近で回転が止まったように見えるため,
見かけのサドルノード分岐がそこに存在しているという意味で「ゴースト」なんて呼ばれることもあります.
ここでは,ボトルネックに費やされる時間を見ていきましょう!
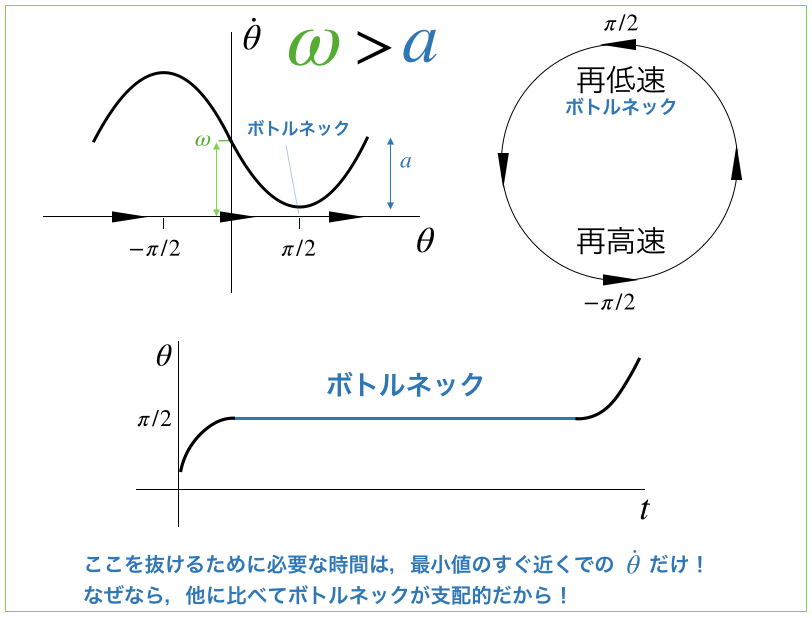
ボトルネックにかかる時間は,一周期 = ボトルネックとします.
上の図からも確認できるように,一周期のうちボトルネックが占める時間がかなり支配的なので,このような近似で大丈夫です.
そこで,ボトルネック付近の曲線を見てみると,二次関数的な近似ができることがわかります.
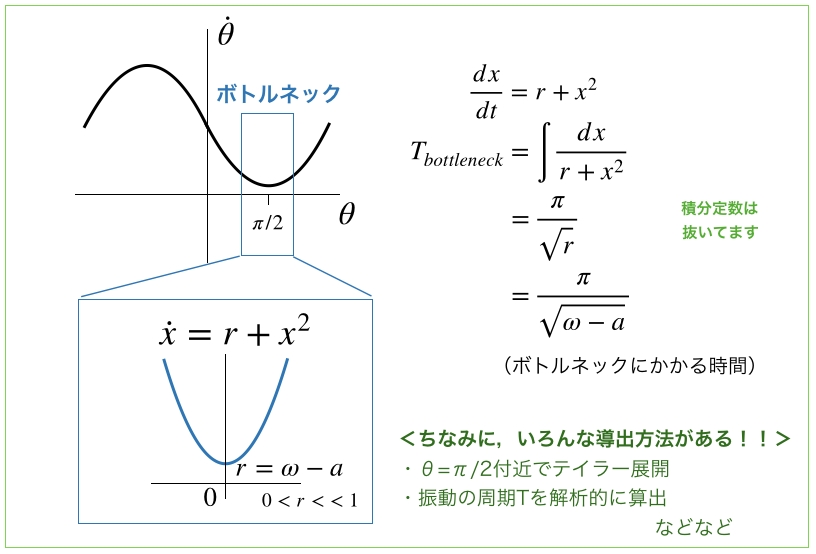
二次関数近似をして,ボトル付近を積分することで,ボトルネックに費やされる時間を見積もることができ,結局これが近似的な一周期の時間となります.
なので,他にもテイラー展開をしたり,普通に振動の周期を算出しても結果はほとんど同様なものになります.
最後に,,,
現在は,1次元ですが,これだけ読めばかなり理解は深まると思いますよ!