- 亜臨界ピッチフォーク分岐について理解したい
- 数学や工学が好き!
- カオスや非線形が好き!
以前,分岐の種類に関しての記事を書きました.
(ダイナミクスのパラメータ依存性を考えて分岐を紐解く)
この記事では,亜臨界ピッチフォーク分岐について詳しくみていきたいと思います.
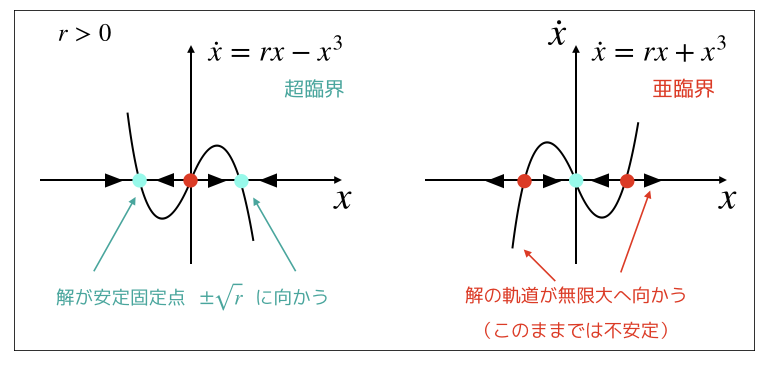
亜臨界ピッチフォーク分岐(3次の項がプラス)の場合,実際の物理系では,3次以上のより高次の項の働きによって安定化がはかられます.
すなわち,5次のマイナスの項を付け加えることになります.
![]()
これが,亜臨界ピッチフォーク分岐の標準系になりますが,今日はコイツをやっていきましょう!
グラフについて
まずは,3次の項と5次の項の影響を見ていきましょう.
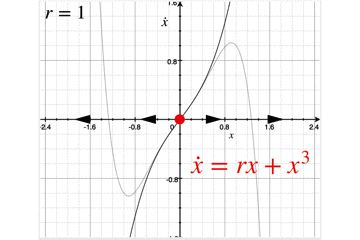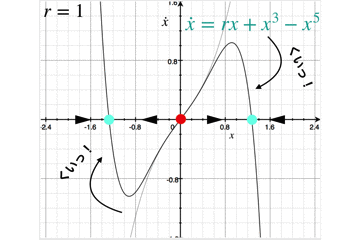
簡単のため,パラメータr=1 の場合の比較を載せています.
5次の項を導入することによって,これまで無限大に発散していたグラフが,折り返しており安定固定点に収束するようなグラフになることがわかります.
超臨界ピッチフォーク分岐的になりますが,5次の項を導入することで,複数の安定固定点が生まれるためジャンプやヒステリシスといった現象が生じます.
そこで,まずは,パラメータr に対する亜臨界ピッチフォーク分岐のグラフを考えていきます.
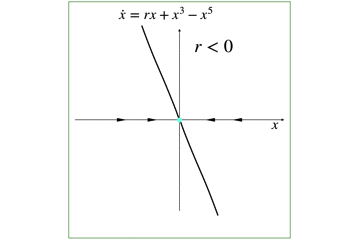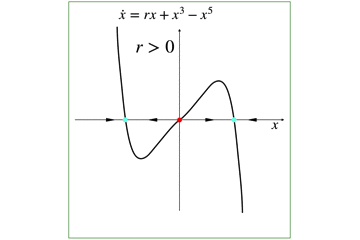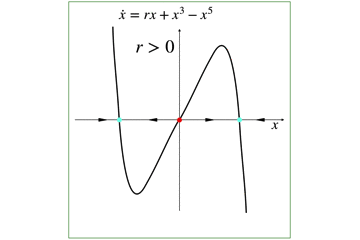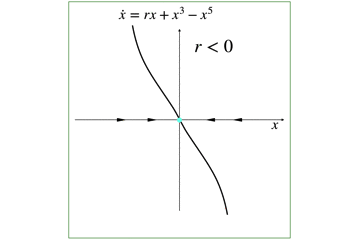
具体的に,パラメータrに数値を入れた時の値は以下です.
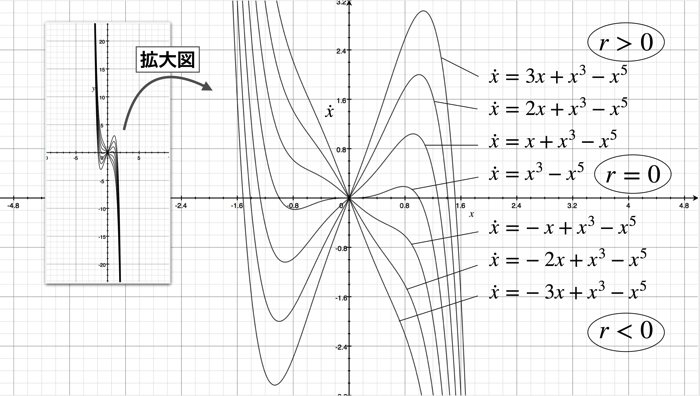
ちなみに,xが小さい項では,5次の項は無視されるほど小さくなるので,分岐に関しては,一番はじめの絵 (rx+x^3) のようになります.
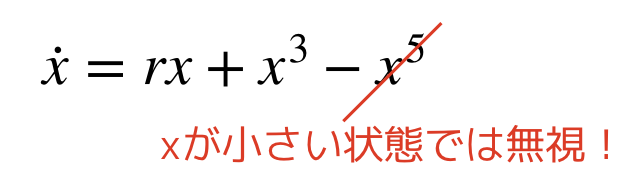
分岐図に関しては?
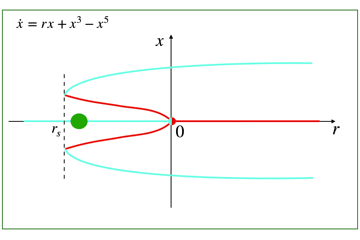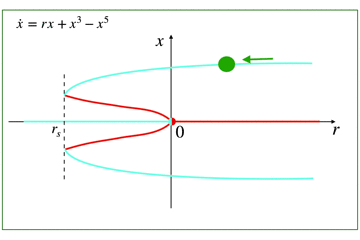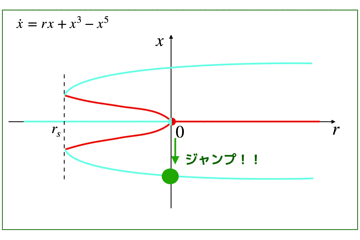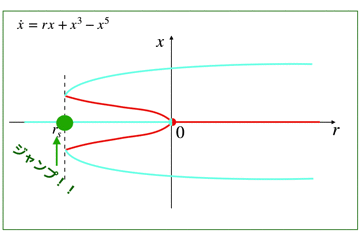
5次の項の影響による亜臨界ピッチフォーク分岐の分岐図は以下の通りです.

5次の項によって生じる新たなことは,不安定固定点がrsで折り返して安定固定点に転じるということです.
ここで,rsは負です.
rs<r<0 の状態では,2つの安定状態を持ちます.そのため,t→∞で,ジャンプやヒステリシスなどの面白い性質を見ることができます.

亜臨界ピッチフォーク分岐図を確認すると,パラメータrの値によって面白いことが読み取れます.
rを負から徐々に大きくしていく場合
はじめにパラメータrを負から徐々に大きくしていきましょう.
系をx0から出発させて,パラメータrの値を負から徐々に大きくしていくと,r=0でジャンプという現象を見ることができます.
r=0は不安定点になり,ちょっとの摂動を与えると原点から上か下か,どちらかの安定固定点に飛びます.
どちらかに飛んだ後,rをさらに大きくしていくと,系の枝に沿って変化していく様子が確認できます.
rを正から徐々に小さくしていく場合
今度はrを正から徐々に小さくしていきましょう.
r=0より小さくなっても,安定固定点のままなので,xの状態は原点にジャンプしません.
このように,パラメータ変化に伴う系の状態が可逆でないものをヒステリシスと言います.
ヒステリシス性があるので,r=0よりももっと小さくなり,r=rsになってはじめてジャンプがおきます.
ちなみに,rsでの分岐は,「サドルノード分岐」です.
サドルノード分岐についてはこちら
おまけ
分岐にはいろんな読まれ方があって,例えば
- 超臨界ピッチフォーク分岐 → 前方(フォワード)分岐,ソフト,連続転移など
- 亜臨界ピッチフォーク分岐 → 反転分岐,後方(バックワード)分岐,ハード,不連続転移など
と呼ばれたりします.
相変わらず参考にした本は「ストロガッツ 非線形ダイナミクスとカオス」です