自分の研究アーカイブ用記事として残しておきます.
(間違っている可能性もあるので責任は持ちませぬ...)
脳波信号(安静時 vs 集中時)を時間周波数解析(時間FFT)して,時間波形から周波数波形に直した時に出てきたピークの値をヒストグラムにして表示します.
つまり,安静時の脳波と集中時の脳波の周波数のピークの推移を見たい.
的な考えで良いと思います.
時間FFTの窓幅は約1秒の矩形窓です.
時間FFT後のピークの値はすでにテキストか何かに落とせているものとします.
以前の記事でプログラムと,やりたいことは公開してます.
gnuplotのコマンドとして以下
軸の設定
1 2 3 4 5 6 7 8 9 10 11 | set xrange [0:240] set xlabel "Time (s)" set xlabel font "Times New Roman, 20" set xtics font "Times New Roman, 20" set yrange [0:30] set ylabel "Frequency (Hz)" set ylabel font "Times New Roman, 20" set ytics font "Times New Roman, 20" set key font "Times New Roman, 20" |
時間窓ごとの周波数ピークの描写
1 | plot "relax.txt" u 1:($6/(2*pi)) w lp t "relax"lc rgb "green", "stress.txt" u 1:($6/(2*pi)) w lp t "stress" lc rgb "red" |
おいらのtxtデータでは,1列目に時間,6列目に固有角振動数(2πf)が入っているので,6列目を2πで割ってグラフに書いてます.
1 2 3 4 | set term jpeg set out "result.jpg" replot set term aqua |
jpegで画像を保存する時のコマンド.
term はterminalの略.
画像の保存が終わったら元のターミナル(aqua)も戻しておきます.
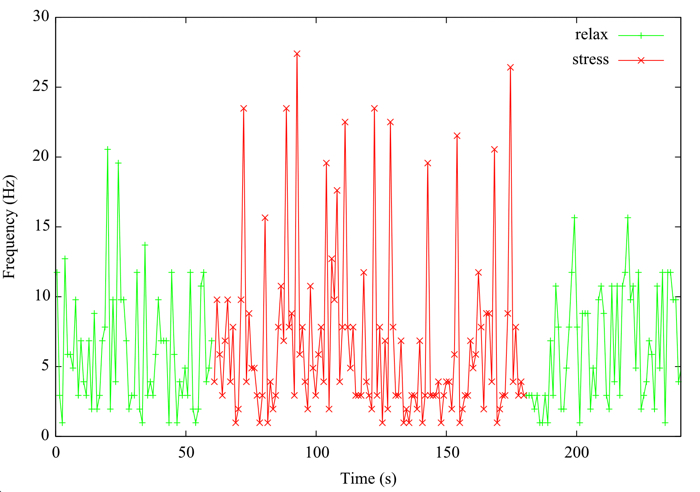
今回は時系列データの60秒から180秒の間で負荷を与えたので,こちらでピーク周波数が高い結果になっています.
実はこれは第1ピークですが,第3ピークまで同様に取得してます.
次に,こいつらをヒストグラムにしていきます.
各ピークのヒストグラムの描写
ヒストグラムの幅を指定して
1 2 | binwidth=0.25*0.5 bin(x,width)=width*floor(x/width)+width/2.0 |
relax.txtを(relax1.txtとrelax2.txt)に分けました.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | set multiplot layout 3,3 set xrange [0:30] set xlabel "frequency (Hz)" set ylabel "numbers" set yrange [0:30] plot 'relax1.txt' u (bin(($6/(2*pi)),binwidth)):(1.0) smooth freq with boxes t "omega1(a-relax)" lc rgb "green" plot 'stress.txt' u (bin(($6/(2*pi)),binwidth)):(1.0) smooth freq with boxes t "omega1(a-stress)" lc rgb "red" plot 'relax2.txt' u (bin(($6/(2*pi)),binwidth)):(1.0) smooth freq with boxes t "omega1(a-relax)" lc rgb "green" plot 'relax1.txt' u (bin(($9/(2*pi)),binwidth)):(1.0) smooth freq with boxes t "omega2(a-relax)" lc rgb "green" plot 'stress.txt' u (bin(($9/(2*pi)),binwidth)):(1.0) smooth freq with boxes t "omega2(a-stress)" lc rgb "red" plot 'relax2.txt' u (bin(($9/(2*pi)),binwidth)):(1.0) smooth freq with boxes t "omega2(a-relax)" lc rgb "green" plot 'relax1.txt' u (bin(($12/(2*pi)),binwidth)):(1.0) smooth freq with boxes t "omega3(a-relax)" lc rgb "green" plot 'stress.txt' u (bin(($12/(2*pi)),binwidth)):(1.0) smooth freq with boxes t "omega3(a-stress)" lc rgb "red" plot 'relax2.txt' u (bin(($12/(2*pi)),binwidth)):(1.0) smooth freq with boxes t "omega3(a-relax)" lc rgb "green" unset multiplot |
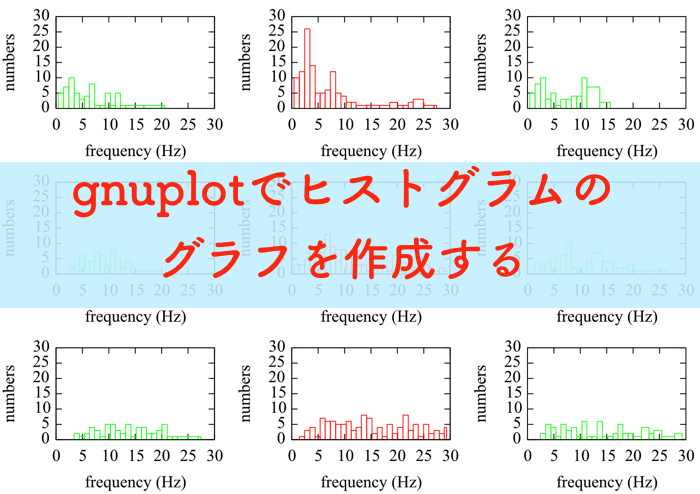
作ったグラフはこちら.
- 上の行3つのグラフが第1ピーク
- 中の行3つのグラフが第2ピーク
- 下の行3つのグラフが第3ピーク
の推移です.
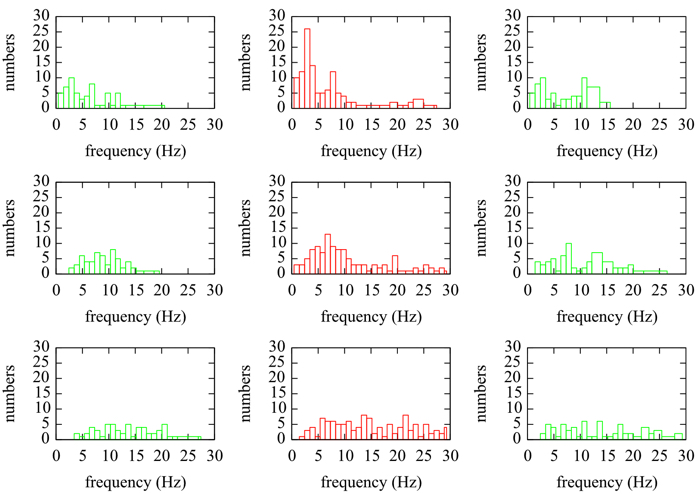
赤で示した集中時(stress)のヒストグラムには,20Hz以上の高い周波数帯域を持つことが確認できます.
やっぱり集中した時の脳波には,高い帯域の周波数が見られるのですね!
しかし,第3ピークになると緑で示した安静時脳波も高い周波数を取ることが確認できます!
パワーはかなり低いですけどね!
(今度パワーも見せます)
終わり!