- バイオメディカル系（工学）の研究をしている人
- 脳波の数学的モデルの研究をしている人
- おいらが読んだ海外の論文のストック
表題の通り，おいらが読んだ読んだ論文をコメントをつけて勝手にストックしていきます．
読んだものを整理して置くのって大事なのです！
あくまで自分用ですが，見たい方はどうぞ！
論文のリンクも貼っておきます．
Emotion clustering from stimulated electroencephalogram signals using a Duffing oscillator
原文はこちら(PDFで読めます)
Duffing振動子を用いてEEG信号の感情推定(クラスタリング)を行なっている文献です.
感情は以下の5つです．
- 怒り
- リラックス
- 喜び
- 悲しみ
- 恐れ
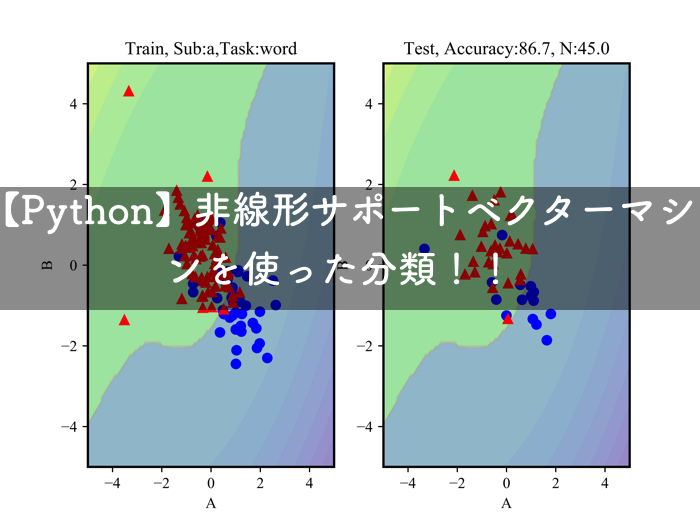
Duffing振動子の外部入力項自体に，脳波信号を入れて，duffing振動子の位相平面を確認するといったようなものです．数値解法はルンゲクッタ法を用いています．
最終的に，サポートベクターマシンを使用してクラスタリングを行なっている．
Duffing振動子のモデルを通して，脳波解析を行うことによって，ノイジーな信号解析をロバストに行うことができるのが大きいメリット．
A Method for Determinism in Short Time Series, and its Application to Stationary EEG
脳波の決定論を時系列アトラクタの法線ベクトルを使いあれやこれやで探した結果，
低次元の決定論的構造は過去の文献と同様に存在しないとことがわかったが，解析時間を短くしたらワンチャンあるかも！という感じでした．
考察で提言があった論文は気になったので，後で読みます．
Glass and his colleagues have employed the Ka- plan–Glass method for deterministic dynamics for an EEG and found that real EEG record is not deterministic [14].
[14] L. Glass, D. T. Kaplan, and J. E. Lewis, “Tests for deterministic dynamics in real and model neural networks,” in Proc. 2nd Annu. Conf. Nonlinear Dynamical analysis of the EEG, 1993, pp. 233–240.
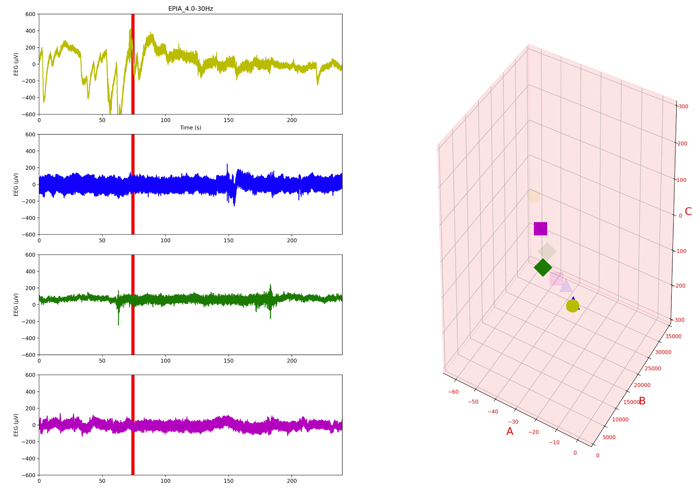
A phenomenological model of EEG based on the dynamics of a stochastic Duffing-van der Pol oscillator network
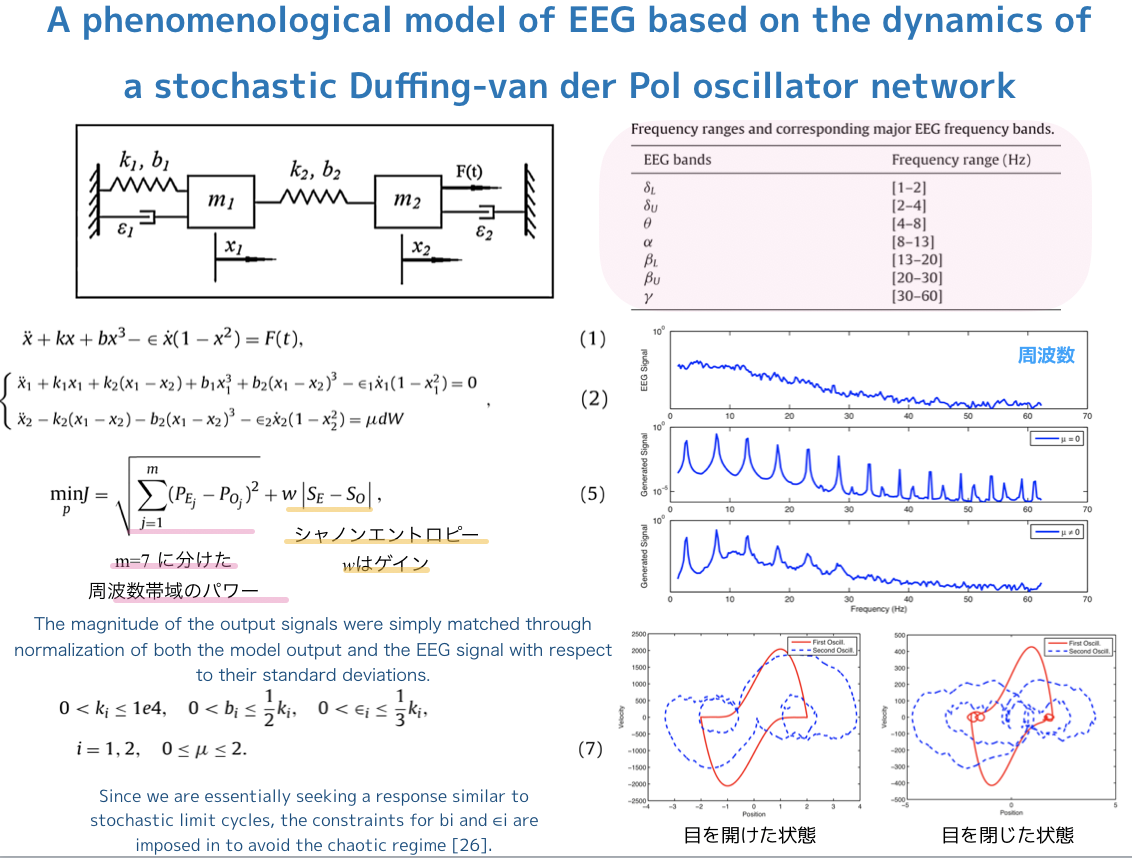原文より適当に抜粋しました．
確率論的 (Stochastic) な数式モデルってなんか惹かれますよね．
しかもDuffingとvan der Polを使ってます．←決定論と確定論の融合だ！
（参考：ダフィング振動子とファンデルポール振動子の時系列アニメーション）
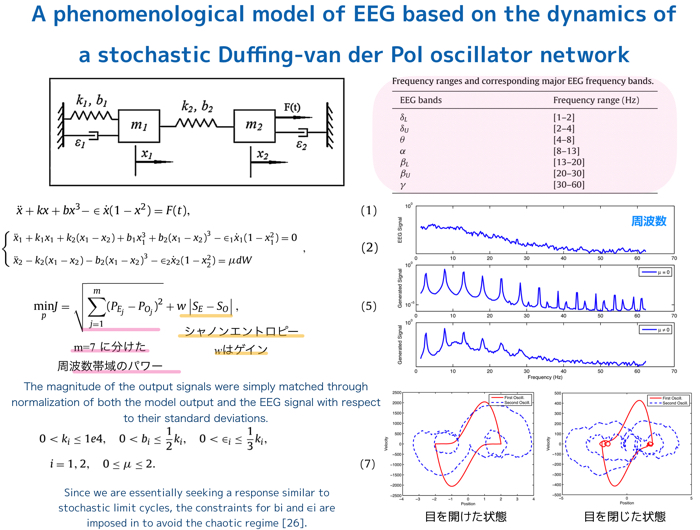
モデルのパラメータを推定し，位相平面より脳波の状態（開眼or閉眼）を解析するようです．
モデルパラメータ推定には，実波形のEEGと非線形モデル出力の周波数特性およびシャノンエントロピ（情報量）が一致するように定めてます．
おいらも脳波の波形を合わせるためのモデルパラメタ同定を行なっていますが，評価関数を周波数とシャノンエントロピで一致をさせているわけではないので非常に興味深い記事です．
また，モデル出力の時系列波形や周波数波形，さらにはパラメタ値まで公開しているので参考になりました．
（気になる人は原文をどうぞ）
しかし実験値の脳波（前頭葉）に関してはちょっと疑いが強い，，，です．
あと，パラメタ同定の誤差がちょっと気になるくらいでしょうか．
同定のアプローチやモデルアウトプットとしては興味深いので真似してみます．
あと，以下は，引用文献で気になったので後で読みます．
（論文の積読がやばいので後ほど調べる！）
子引き孫引き地獄！！！
Analysis and modeling of time-variant amplitude–frequency couplings of and between oscillations of EEG bursts
Duffing振動子による脳波のモデリングをしてるのですが，低周波と高周波帯域を模擬するために式を2つ（u，v）用意しております．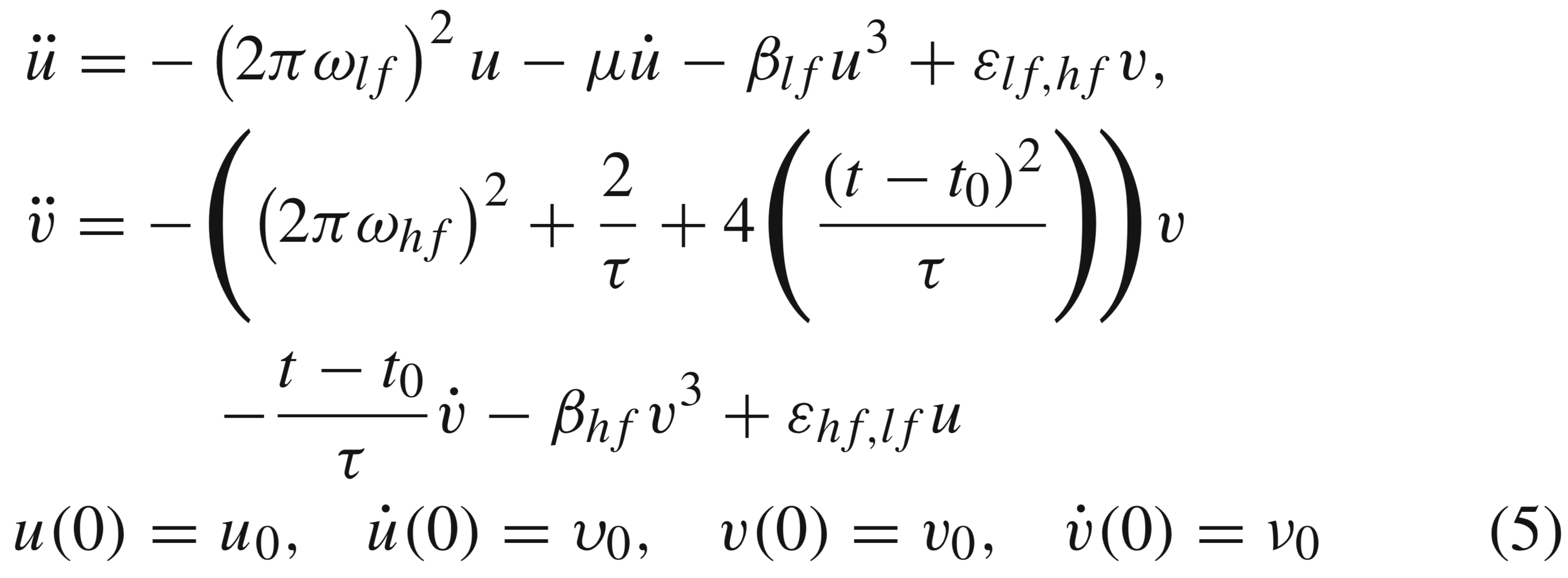
パラメタ同定をするときの目的関数は以下です．
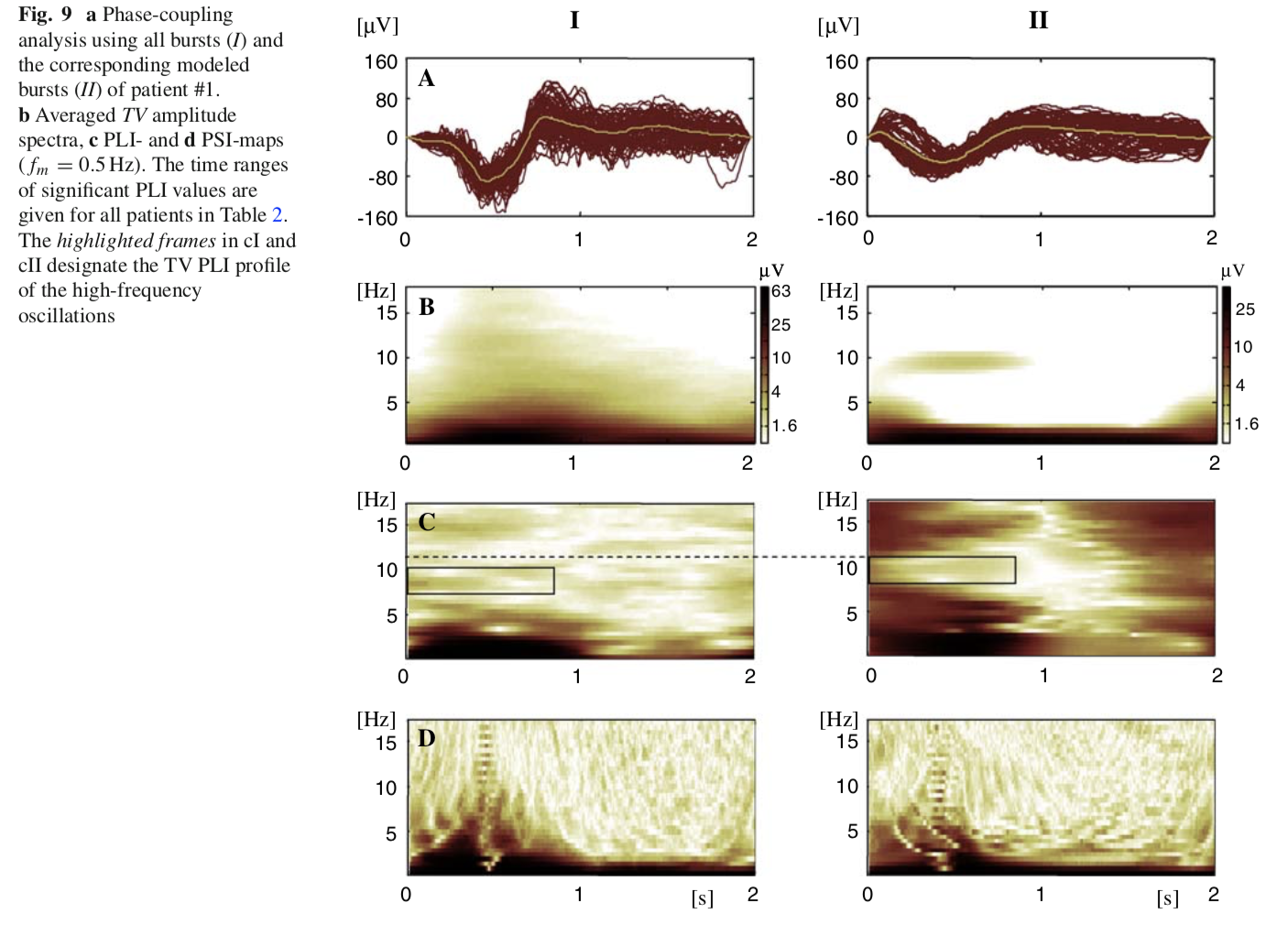
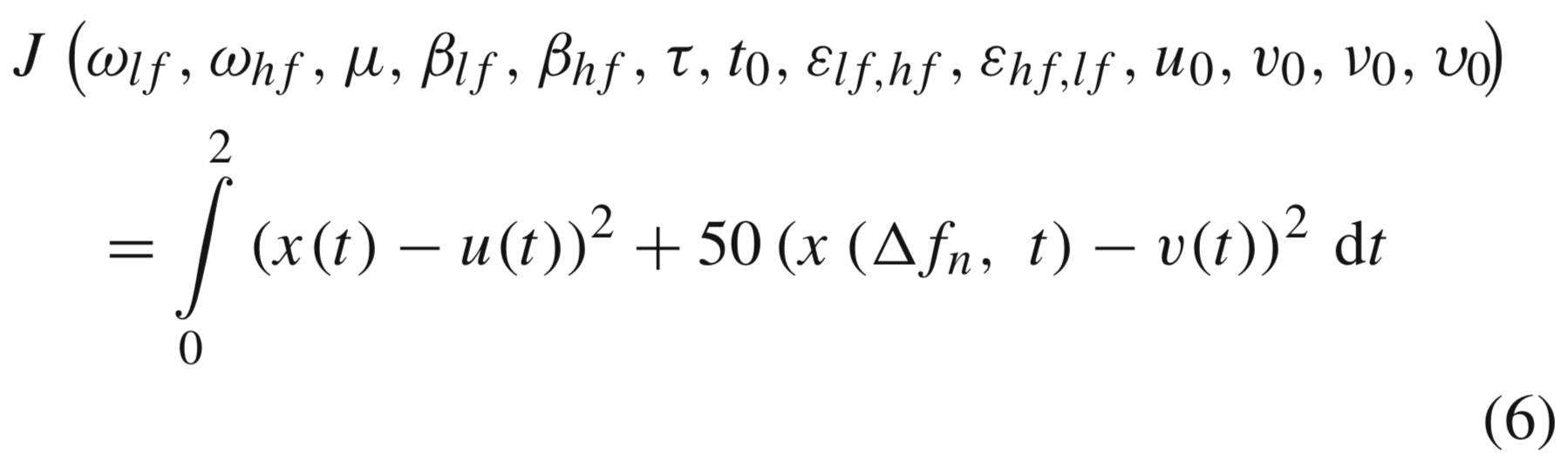実験データの脳波データは，脳波がバーストしている箇所を解析しているようですが，解析結果の図が多過ぎてちょっと混乱状態になったので，一旦飛ばします笑
詳しくは原文を読んでください！
（見てくれ綺麗ですが，あんまり画像の色彩データを結果として表示するのは好きではない派です）
Coupled oscillators for modeling and analysis of EEG/MEG oscillations
いくつか連成された非線形振動子を使ったEEG/MEG解析の研究ですね．
（新生児の睡眠EEGや，体性感覚野のMEG，鎮静患者の異常脳波）
モデル化することによって，脳波データの隠れた特性を探すことを目的としています．また，いろんな種類のデータを使用し，適宜モデルを更新していくことによって，多種多様なデータ解析を可能にするようなことが書かれています．
しかし，モデル中のパラメタは66個もあり，モデルパラメタ同定は結構難しいような印象を受けました．
低周波(1.0~1.6 Hz)では上手くいっている様子ですが，高周波（3.5 ~ 6.0 Hz）の波形はなかなかチャレンジングらしいです．
おいらは30 Hzくらいの波をやろうとしているのだけど，，，それはやばいのですね．．
以下の画像は，論文からの引用です．
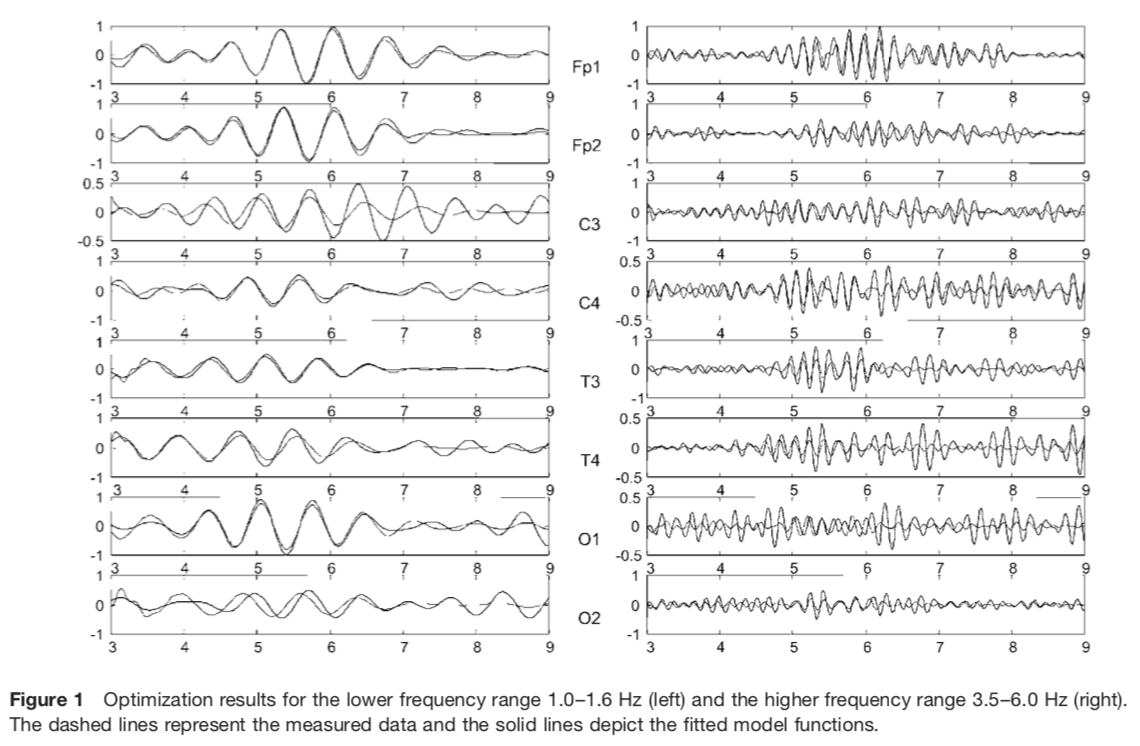
他にも色々と結果がありましたが，ちょっと方向性が違ったのでこの辺で．．．
Estimation of coupling between oscillators from short time series via phase dynamics modeling: Limitations and application to EEG data
原文はコチラ
これちょっと面白そうです．
なんとなくの邦題は”位相ダイナミクスモデリングによる短時間系からの振動子間結合の推定：EEGデータの限界と応用”（Google 先生8割）ですかね．
てんかん脳波の推定に2チャンネルの脳波データ用の非線形振動子を提案して，その結合の強さを評価パラメータにしている研究ですね．
モデルは，白色雑音を入れた非線形振動子で，短い時間の解析窓を用いてパラメタを調べるようです．
本当は，実験データから直接位相を求めたいようですが，位相を計算するためのいくつかのモデルパラメタを同定し，非線形振動子の挙動による観測結果の方が議論しやすいらしいです．（同定値が出てくるので）
しかし，どうしてもフィッティング誤差が出るので，ホワイトノイズを入れ込んで，誤差分を観測ノイズとして考慮してます．
ファンデルポールとダフィングを用いたモデルは以下のようです．
（以下は本文からの引用です）
ノイズの混入モデルに関しては，色々と検討したいところなので，この論文のガウシアン白色ノイズを参考にします．
Fractional dynamical model for the generation of ECG like signals from filtered coupled Van-der Pol oscillators
この論文は生体信号の細かい話がすごく調べられてて参考になります．
生体信号の数学モデリングがなぜ大事なのかを理解したかったら一度じっくり目を通してみても良いかもしれません．
この論文では，心電図ECGに関するモデリングの検証をしているようです．
このような心電図ECGのモデリングの一般化は，正常および異常な心臓状態における脳波信号発生の背後にある生理学的プロセスを理解するのに有用だと言ってます．
現実的な脳波信号を表すためのファンデルポールのモデルパラメタを推定するための最適化手法についての言及もあります．
Is the EEG a strange attractor? Brain stem neuronal discharge patterns and electroencephalographic rhythms
EEGはストレンジアトラクタを形成するのか？また脳幹神経細胞の放電パタンとリズムに関しての論文ですね．
このような疑問詞により訴えかけのニュアンスが入る題目，好きなんですよね．
遊び心あってセンスいいなーなんて思います．
ちょっと古いですが，整理されていて内容も面白いと思います．
脳波の時系列パターンの規則性というのは，しばしばアトラクタなんかで議論されることが多いです．
決定論的動態（一種の規則）を，どの時間かつどの次元スケールであれば追うことができるのかという問題は，数学をやっている人からも関心があるようです．
本当は，そういう規則性を見出して，社会的もしくは医学的にメリットがあれば良いですが，，，，
（例えば相関次元で診断しますっていうのは研究レベルでしょうね．）
この論文のちょっと面白いことは，ストレンジアトラクタではなくて，振動モード的な観点からの観察を行います．
振動工学を学んだことがある人であれば，モードというものはピンとくるのではないでしょうか．
タイヤとか鉄の棒とか振動数によって1次のモードとか，2次のモードとかありますよね．
この時，対称性があるかないかとか，，，生物は難しいんですけどね．
追記
現在，積まれている論文をざっと読んでますので，，，まだまだ加筆していきます．
