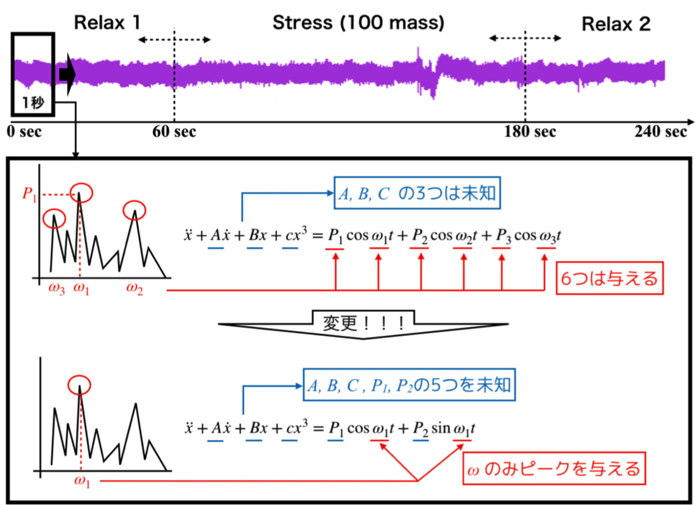
研究用アーカイブですが,モデルのパラメータを最小二乗法でそれっぽく同定することをひたすらやっています.
モデルは,非線形の3乗項を持つDuffing振動子です.
脳波の実験データから逆問題を解き,ヒトの状態を推定したいのですが,どのようなモデルが適切か分からないので,色々と式を弄ったり,検討する周波数帯域をいじったりして,解析結果を眺め考察するという作業をひたすらやりまくっています.
前回までの結果はこちらから.
(参考:Duffing振動子のモデルパラメータを最小二乗法で実験的に同定してみる)
2018年12月22日にデータの一部が間違っていたので更新してます.
さてさて,冒頭で書いている脳波用モデルがどのようなものが至適か分からないので今回も色々と試してみます.
まずは前回使っていたモデルの変更(修正)を行います.
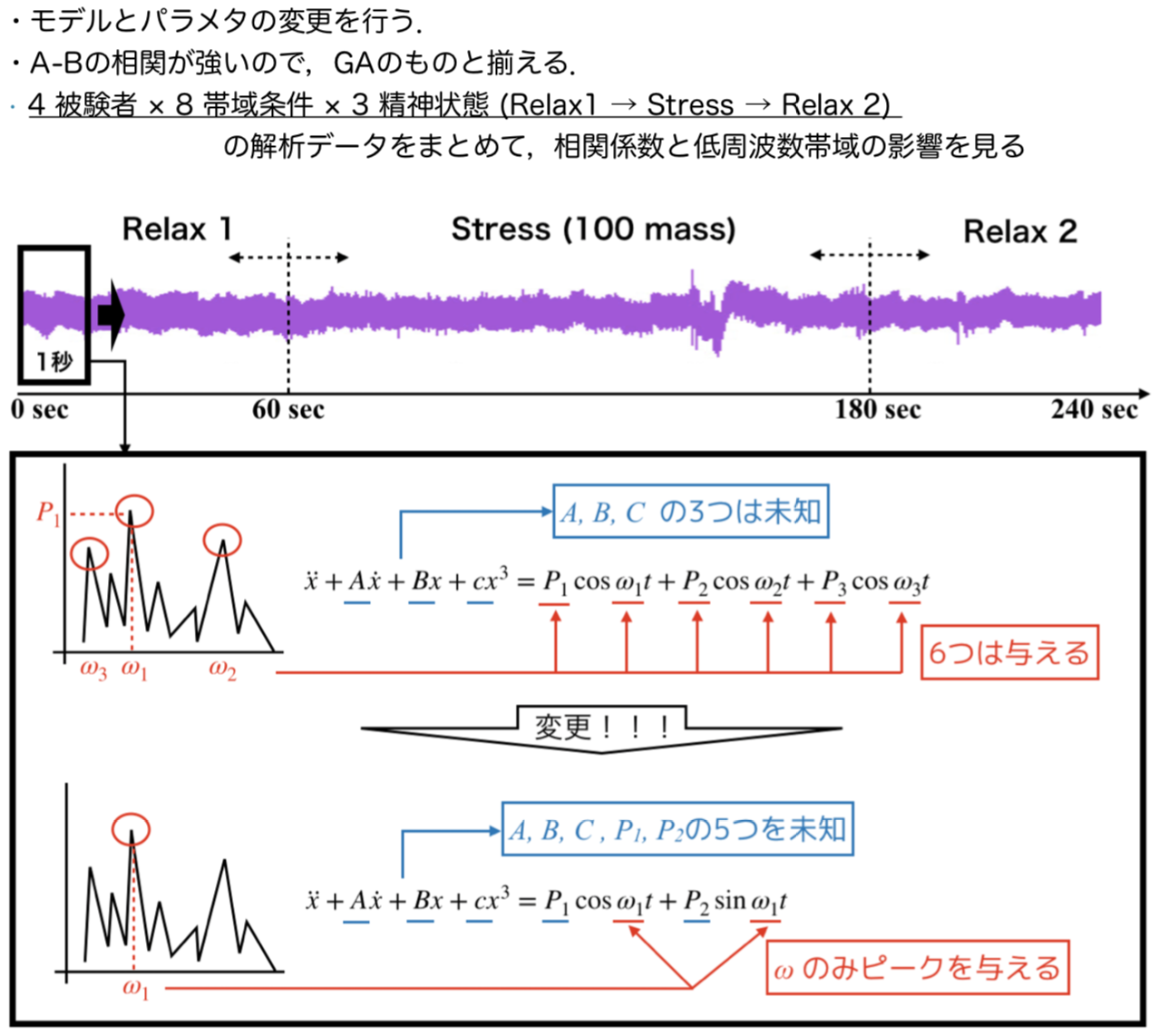
考慮した点は以下です.
- 位相差を加える(sin項)
- 振幅はパラメータ同定する
- 考慮する周波数のピークを第一ピークまでにする
- どの周波数帯域でパラメタ同定をしたら良いか調べる.
(条件①〜⑧)
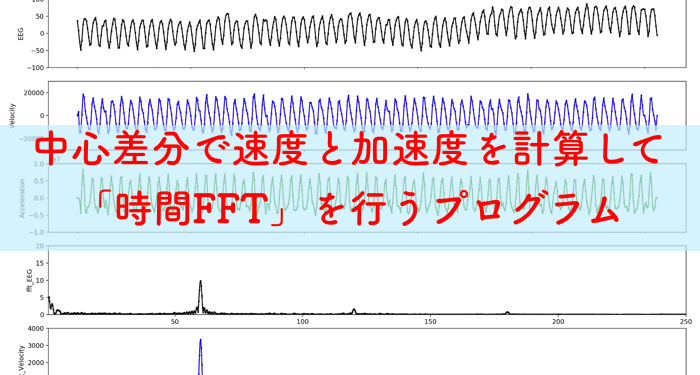
これで1秒毎に内側のモデルパラメタ5つを同定していきます.
時間的に周波数解析も行なって,モデルで使用する各周波数も与えます.
(参考:「時間周波数分析とは!?」)
どの周波数帯域でパラメタ同定したら良いか分からないので,めんどくさいですがゴリゴリ調べないといけません.
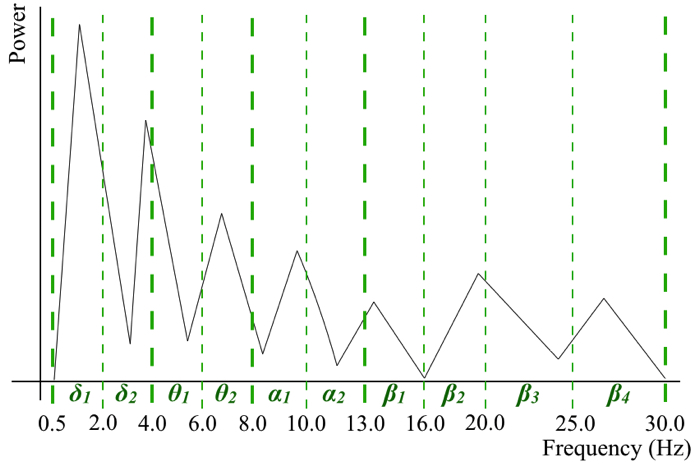
脳波の周波数には帯域別に生理学的な意味合いがあると言われています.
だいたい 0.5 ~ 30.0 Hzなのですが,超低域の 0.5 ~ 4.0 Hzはパワーが高いので解析の際に少し邪魔です.
なので,逆問題を解くようなパラメタ同定する場合,ヒトの生理的特性を同定したいので,低周波数側の影響度を調べるためにも,そこは細かく調べなければいけません.
よって,以下のような8つの帯域条件を調べることにします.
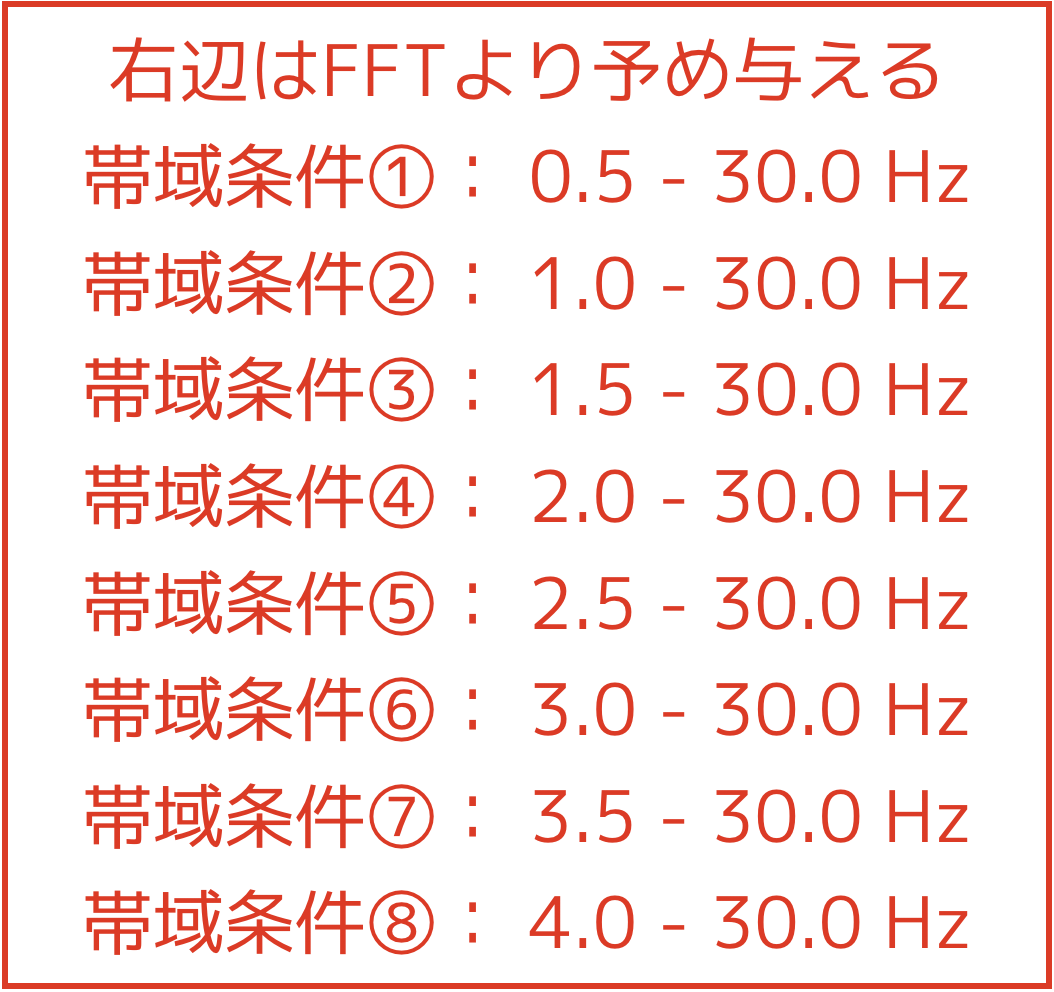
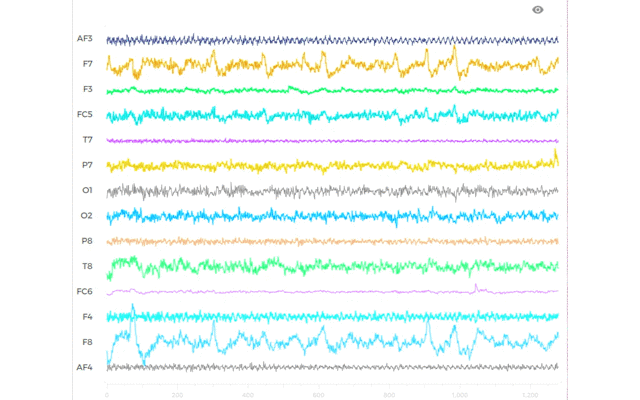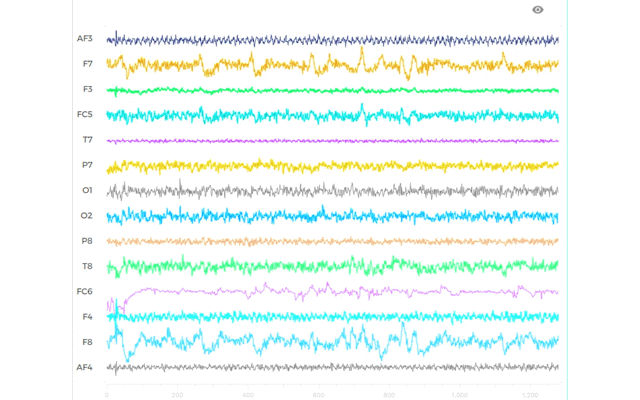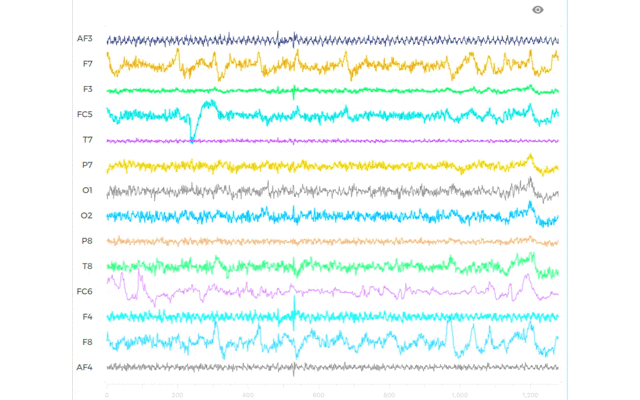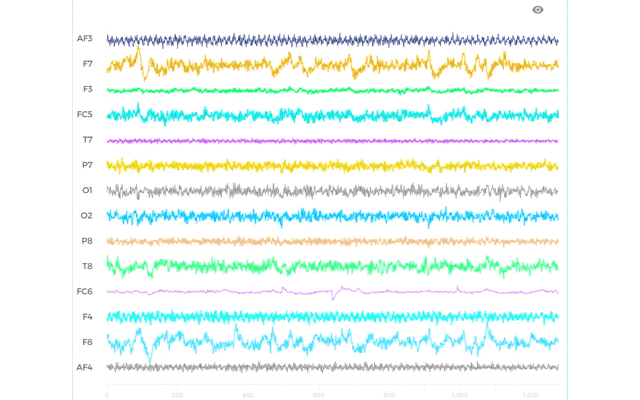
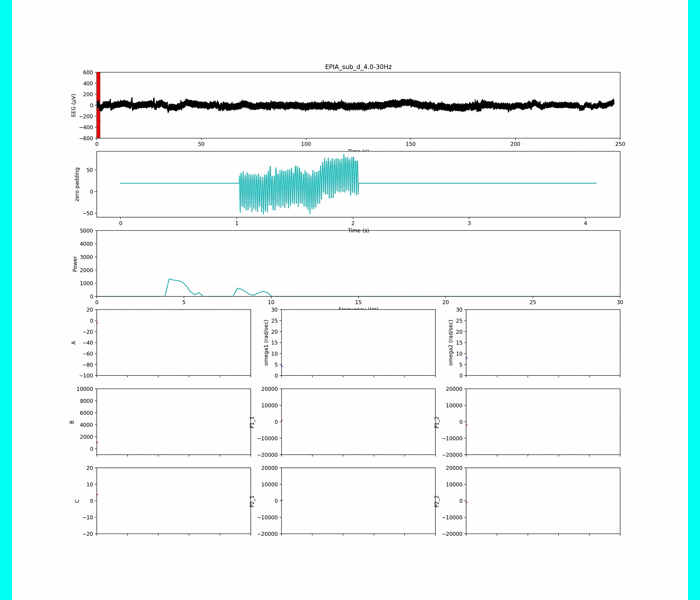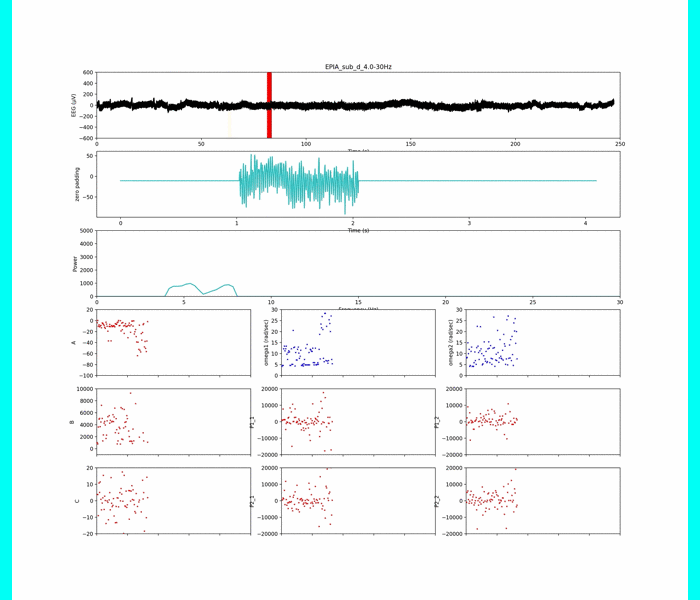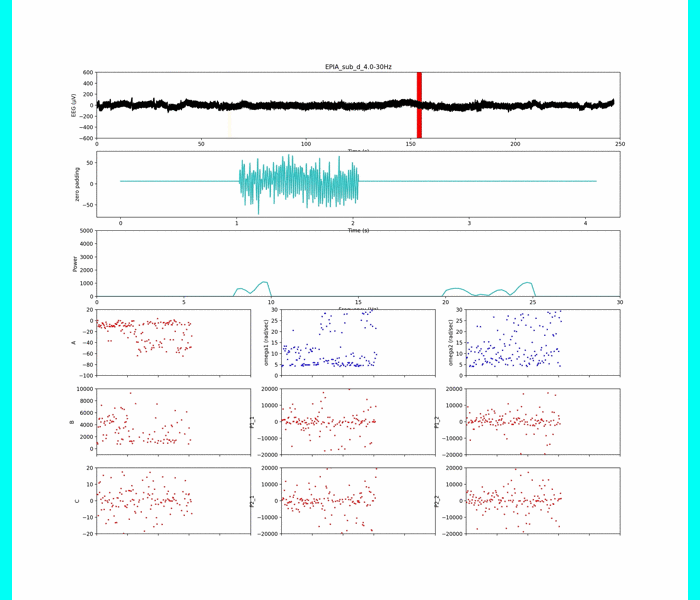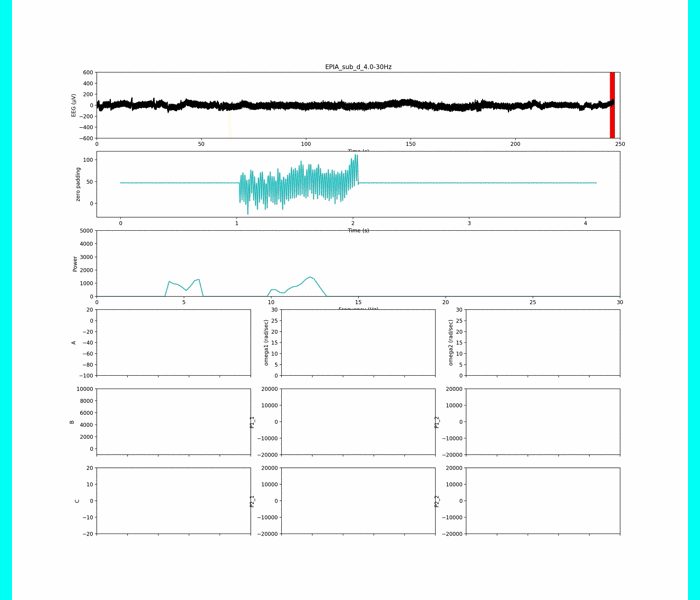
この条件で全てパラメタ同定します.一例として,被験者1の0.5 ~ 30.0 Hzの帯域でパラメタ同定した結果を示します.
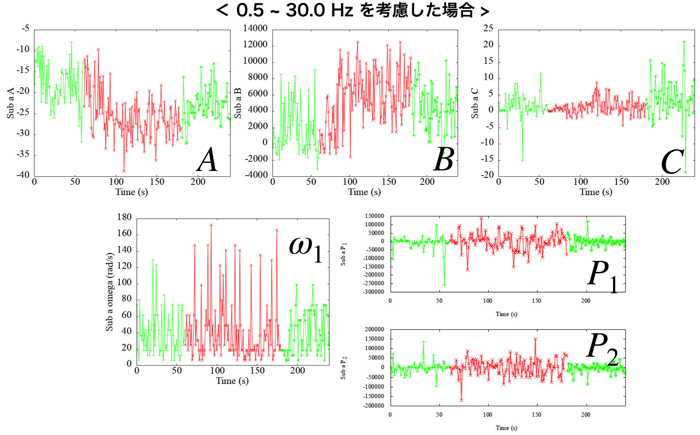
Aは集中時には低下し,Bは増加,Cは0付近に近く,振幅Pは増加,という結果になりました.
このパラメタ同定を8つの条件,全ての被験者で行います.
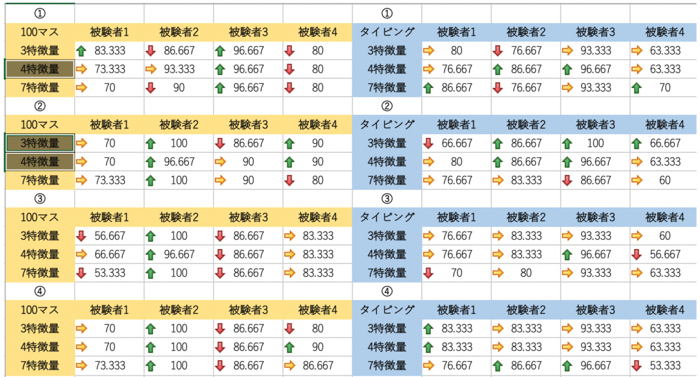
以下の結果は,全ての同定が終えた後の,パラメタA,B,Cの相関係数です.
検討する周波数帯域によって,パラメタ同士の相関はどのような様子になるのか調べました.
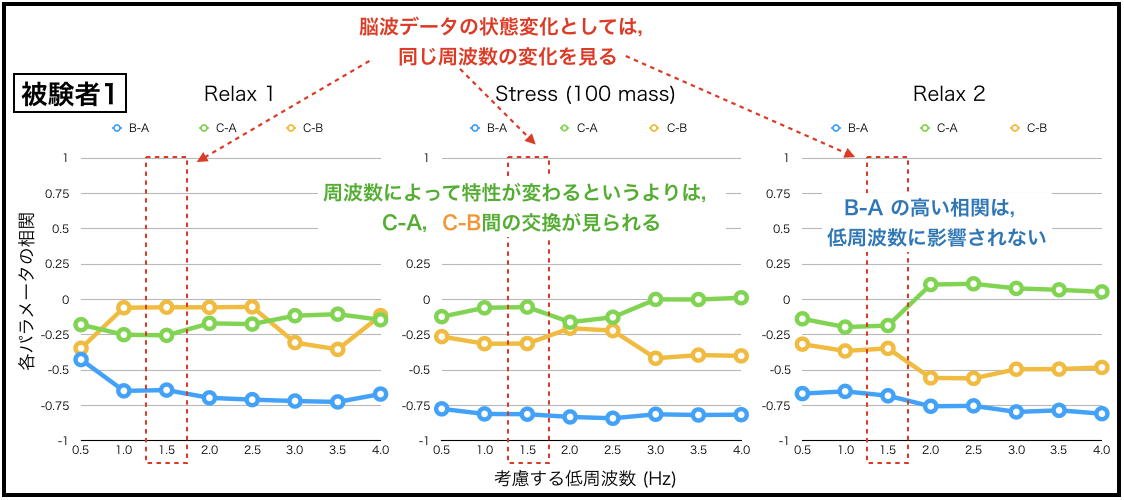

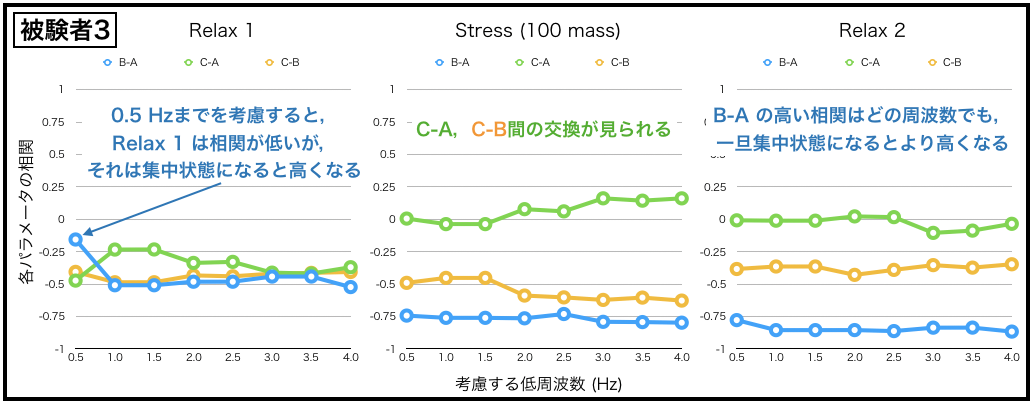

全ての横軸は,検討している周波数(8つの条件)の最小の値です.
例えば,検討している周波数帯域が1.5 – 30.0 Hzであれば,表記を1.5としてます.
最大側の30.0 Hzはどの条件でも変わらないので...
縦軸は,各パラメタの相関値を示してます.
どのような場合でも,パラメタA-Bの相関はかなり大きくて(負),特徴的な値であるという結果になりました.
実は,パラメタAとBは線形項のパラメタなのであんまり嬉しくないのですよ.
脳波の非線形性の把握をちょっとやりたいところなので,きちんと非線形強度を示すCの値の特徴をどうにかして探したい!
というのが,興味の1つでもあります.
問題点は色々とあるので以下を検討していきます
- 周波数帯域(~ 30.0)が広すぎるのか?
- 最小二乗法の同定がだめ?
- FFTの窓関数(矩形窓)がだめ?
- Running windowの幅やオーバーラップ?
- 周波数分解能をもっとあげないとだめ?
- モデルがだめ?(van der Pol型を入れるか)
などなど,色々とあります...
引き続き調査をしていきます...