最小二乗法によるパラメータ同定奮闘記6 〜サポートベクターマシンの試し〜

今日も自分用の研究アーカイブとして残しておきます．
分かる人，見て面白いと思える方だけ適当に読まれてください．
前回，パラメータ同定した結果に対して，サポートベクターマシンを実装して，状態判別（安静VS集中）をしていたのですが，あまり結果が良くなかったです．

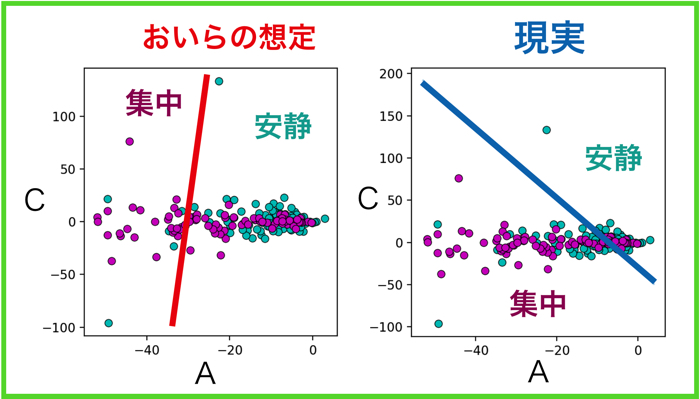
成績でいうと，60パーセントくらいの正解率だったので，まだまだですね．
パラメタ自体が，そもそも二つの状態に分けられるという前提が必要だと思うのですが，そういう特徴量の取り方をしていないですね．
反省です．．．

つまり原因として，安静時と集中時の特徴量（モデルパラメータ）が上手く分離していない（特徴量設計ができていない）ということなので，

これがある程度解決したら，SVMのアルゴリズムも強化できるし，色々とハッピーになるのかな，，とか思っていたりします．

今回の改良

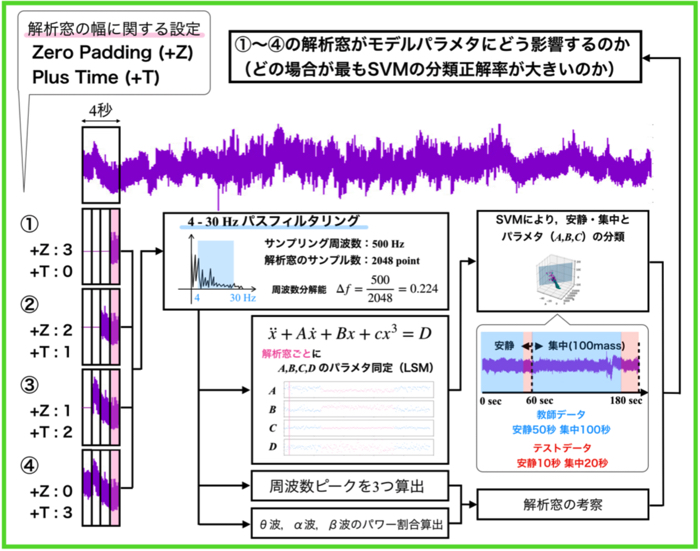
今回の内容は，特徴量設計ができていなかったので，もう一度パラメタ同定を見直すです．

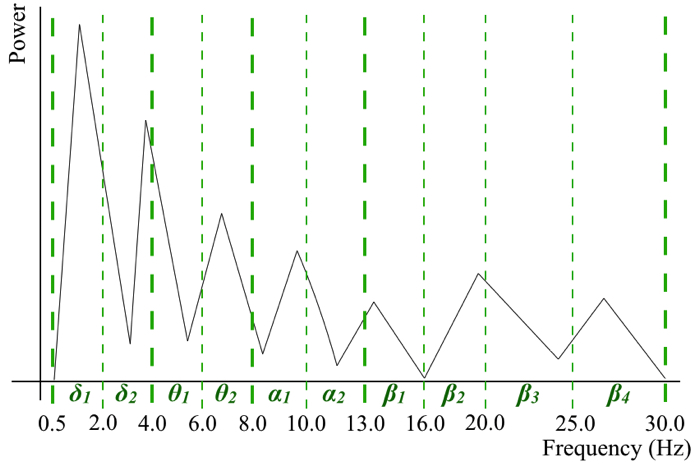
前回のデータは，モデルパラメタを決める際に，解析窓毎の支配的な周波数でIFFTをして決めていました．

しかし今回は，4-30 Hzの帯域でモデルパラメタ同定をしていこうかと思います．

かつ被験者は4人．
サクサク全体のデータをやっていきます．

結果

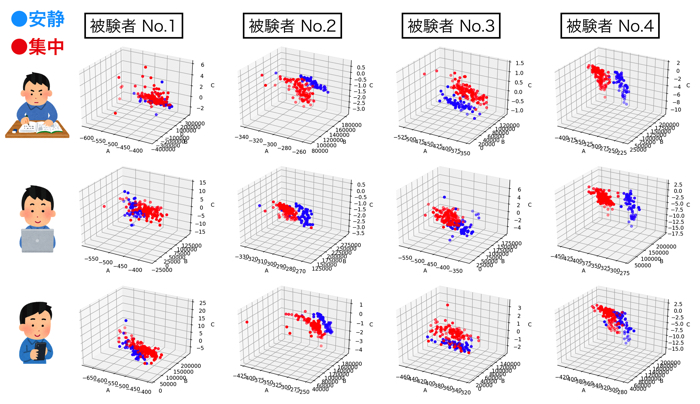
さっそく各被験者(N=4)のサポートベクターマシンの分類結果を見て行きましょう．

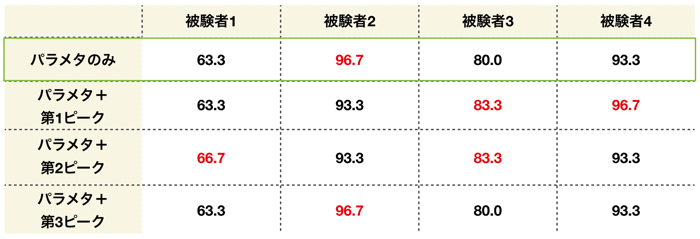
こちらがサポートベクターマシンによる正解率の表です．
パラメタのみという行がとりあえず，下のグラフの正解率をしまします．

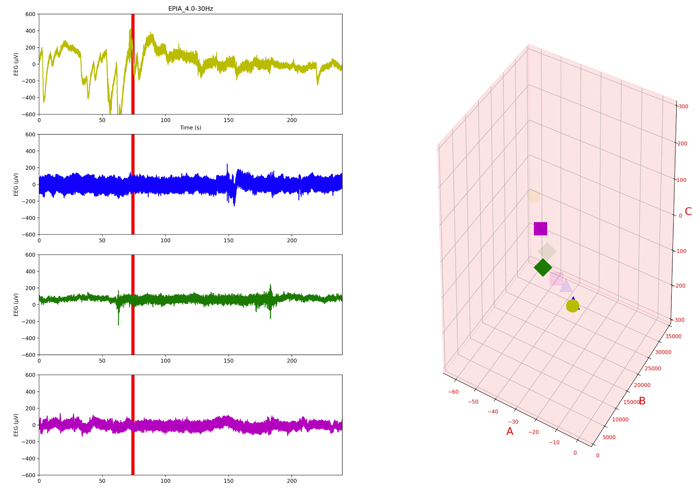
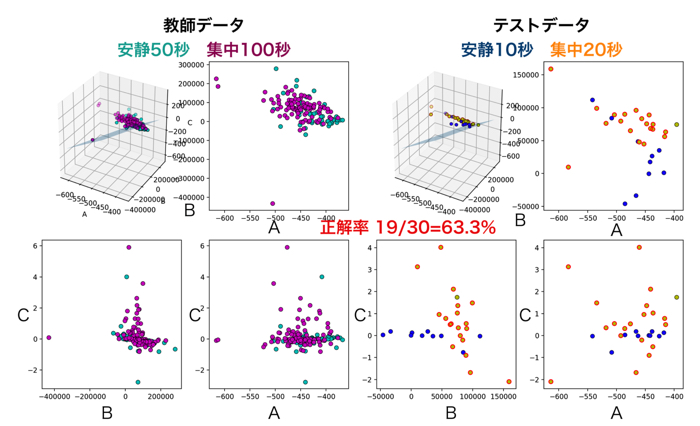
被験者1

被験者2

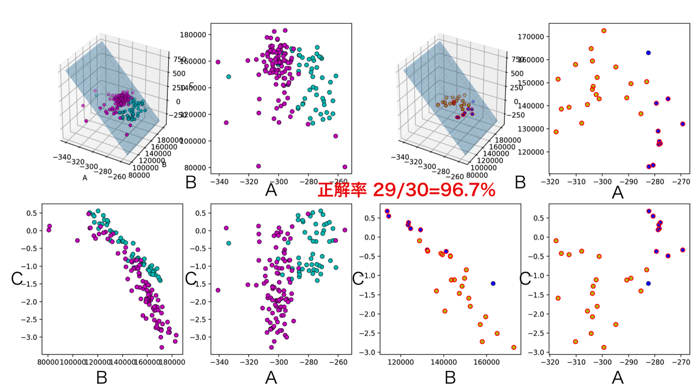
被験者3

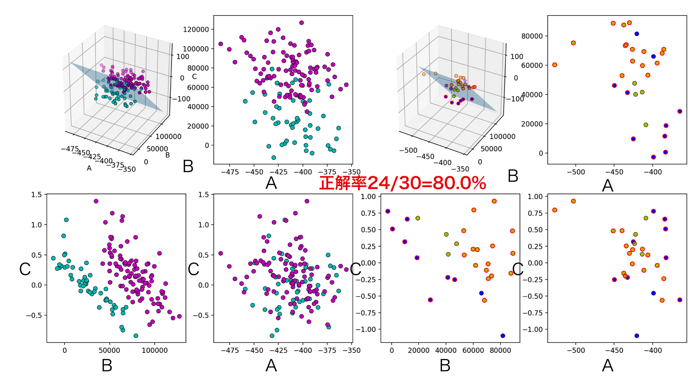
被験者4

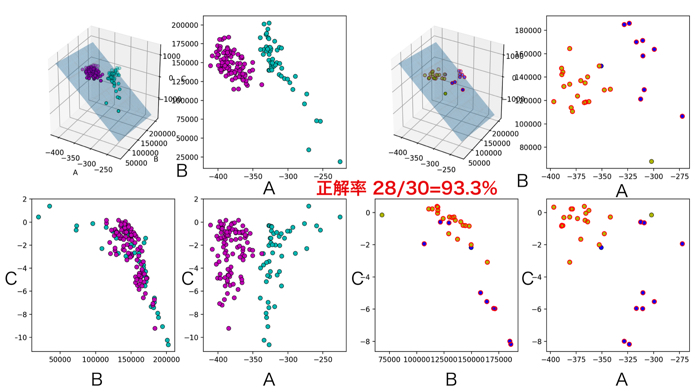
各被験者の特徴量に関して

今回のパラメタ同定では割と正解率が高かったのでないでしょうか．
SVMを使う際の特徴量としては良い感じです．

表の第1~第3ピークというのは，解析窓内の周波数ピークですね．
こいつを含めて，特徴量を高次元のデータにしてSVMをして結果です．

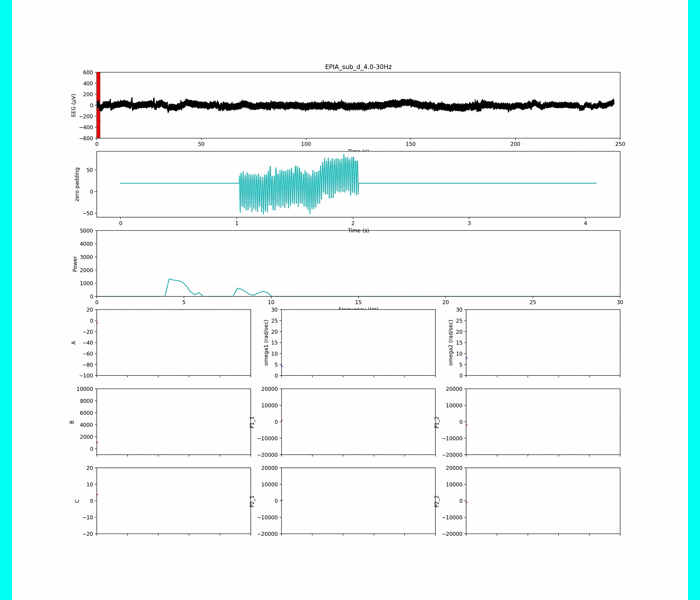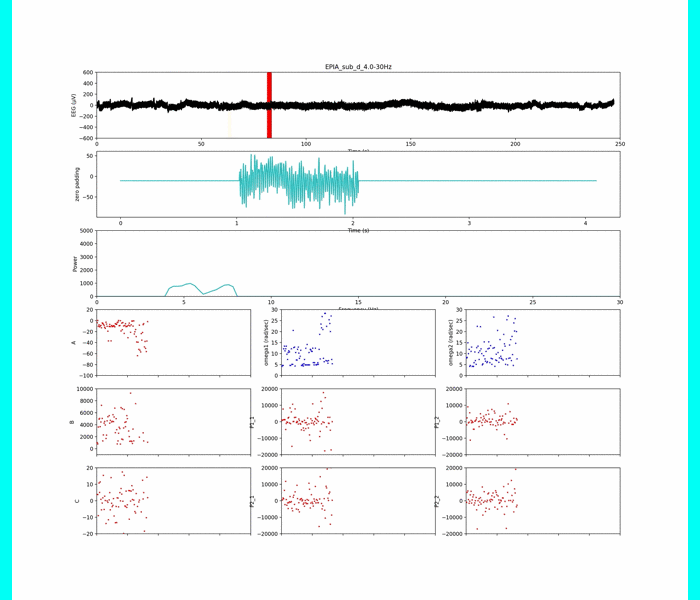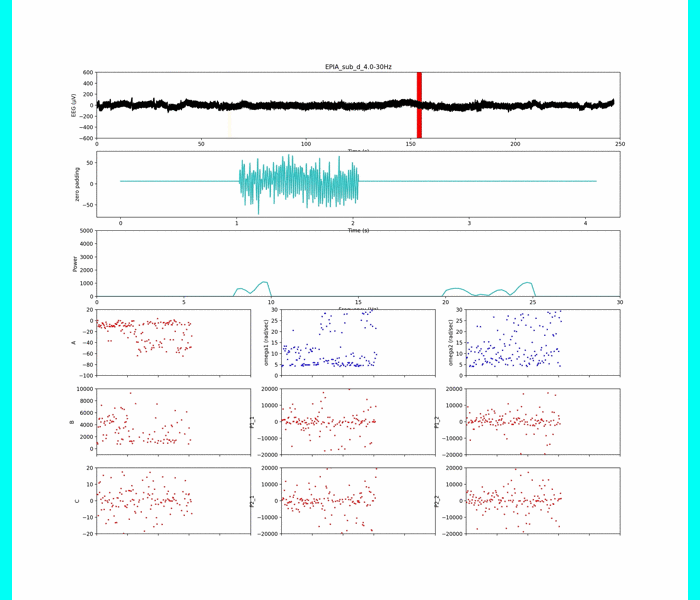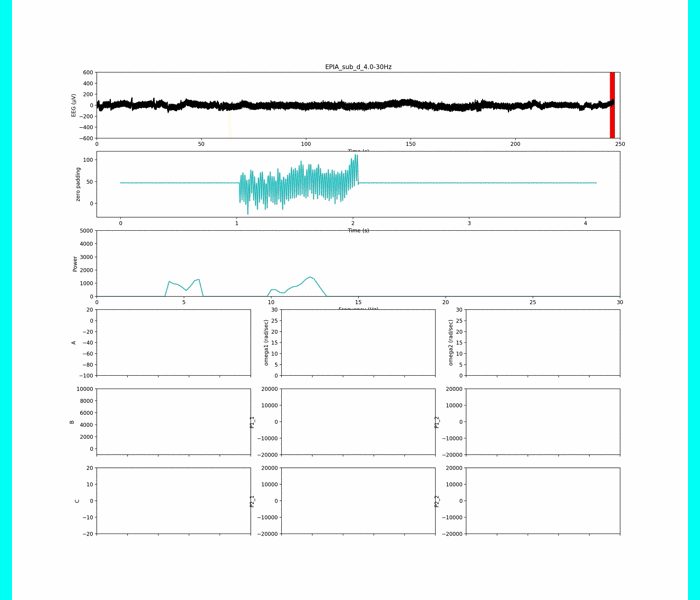
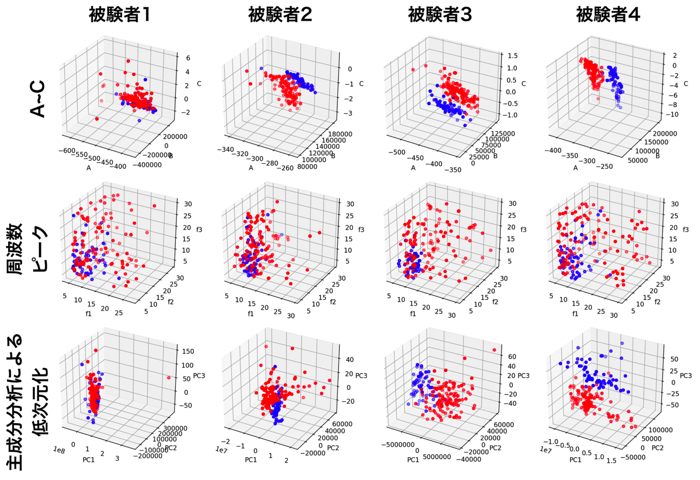
ちなみに，各パラメタと，周波数ピークの関係はこちらです．
下の図は，主成分分析を行って，低次元化しました（グラフ可視化のため）

上の行：各被験者に対するモデルパラメータ
中の行：解析時間窓ごとピーク
下の行：主成分分析による低次元化
（A~C,D＋ピーク3つの７次元のデータを3次元に！）

周波数結果は入れても入れなくても結果は変わらなかったので，モデルパラメタのみで分類ができるか引き続き調査です．

来週もがんばるぞー！

今回の解析に使ったプログラムは要望があればUPします．