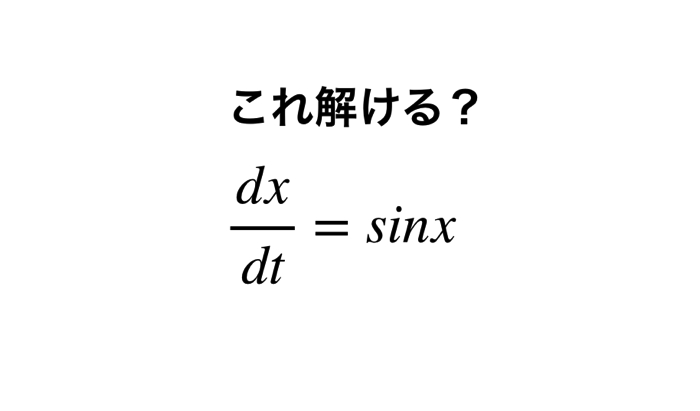
- 「最急降下法」を理解したい人
- 「最適化」に関しての定義を理解したい人
- 数学や物理,自然科学分野の方
こんにちは.けんゆー(@kenyu0501_)です.
今日は,最適化手法「最急降下法」についての解説を行います.
先ずはじめに,最適化についての定義の説明をした後に,最急降下法の説明をします.
具体例を踏まえて実際の関数最小化問題を解いていきます.
解説動画と解説資料
10分くらいの解説動画と,その資料をアップしているので,チャチャっと理解したい人は見てください.
おいらの動画は,話すスピードが遅いので,2倍速で見ることをオススメしてます.
動画解説
解説資料
「最適化」とは!?
先ずはじめに,「最適化」についての理解を深めていきます.

最適化の定義は,「目的に対して,条件内でもっとも適切な計画を立て設計する」ことです.
ここで大事なことは3つあります.
- 目的の設定
- 目的を数値化するための計量的な変数を設定
- 条件を把握しておく
ということです.
アルゴリズムに関しては,以下です.

この最適化を図る上で,どのような計画でこの問題を解くか,に関してはアルゴリズムの話になります.
今回やるアルゴリズムは「最急降下法(SDK)」ですが,他にも色々なものがあります.
例えば最小二乗法(LSM)だったり,「ダウンヒルシンプレックス法(DHSM)」だったり,「遺伝的アルゴリズム(GA)」だったりします.
具体的数値で最適化を理解する
先ほど最適化を解く上で重要な3つの事項に関して,実際に具体的な問題を当てはめて理解度を高めましょう.

目的には,問題を解くための関数が入ります.
今回は2変数関数を定義しました.
$$f(x,y)=(x-1)^4+(y-2)^2$$
ですね.
だいたいは,この関数系を最小にしたり,最大にしたりするような問題を解くことになります.
関数を「最小」もしくは「最大」にするためには,内側の設計変数(\(x\),\(y\))の値を適切に定めなければいけません.
また,今回行う最適化に関しては,条件がついています.
条件とは,「\(x\)と\(y\)の範囲」です.
無限な範囲で考えていたら,解がいくつも出てきてしまう恐れがあるので,制限します.
では目的や変数,条件を確認したら,次はその問題を解くためのアルゴリズムに移っていきましょう!
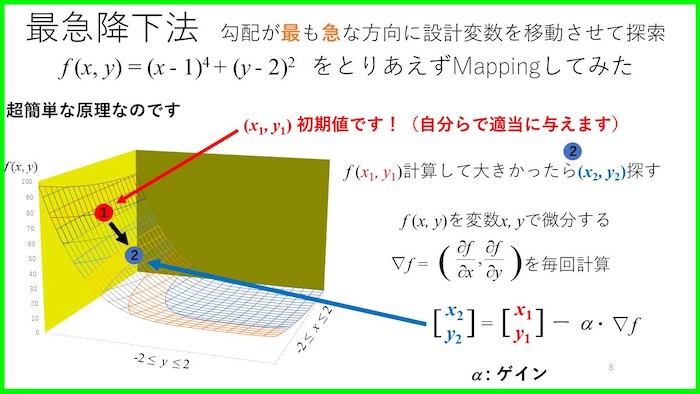
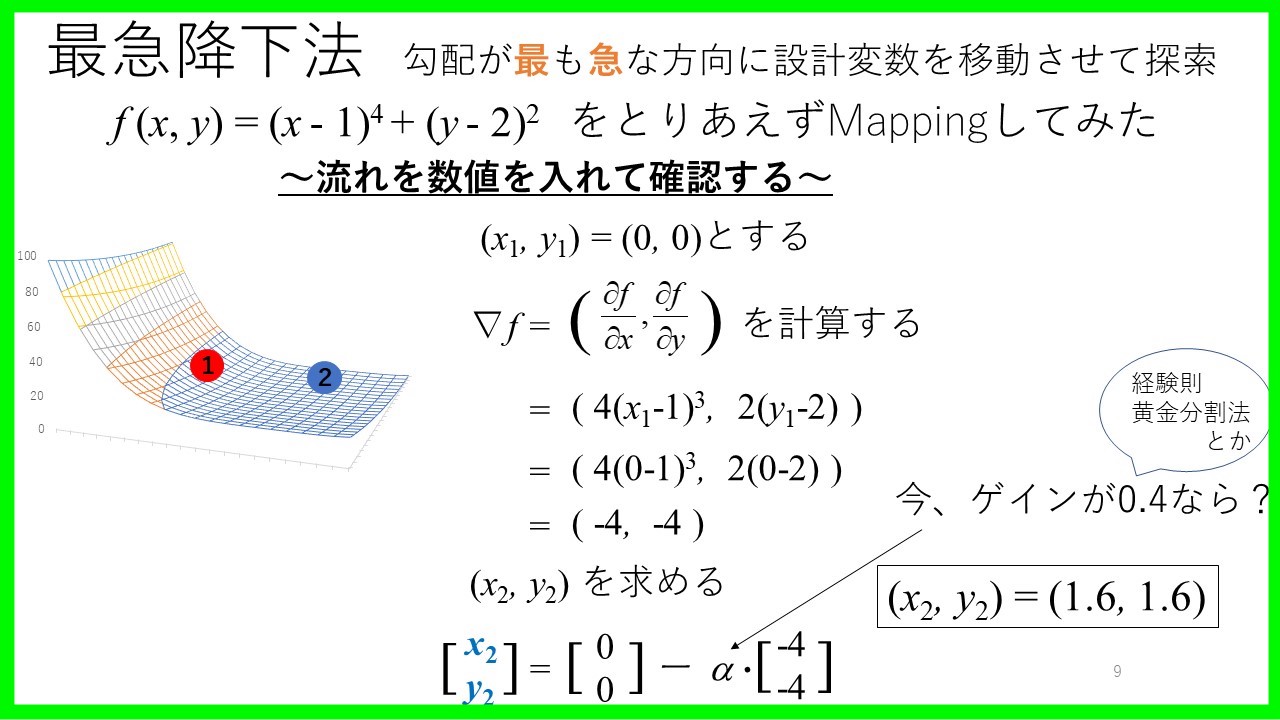
最急降下法

最急降下法とは,「目的関数の勾配(微分)を解いて,傾きに従い内側の変数を移動させて探索する方法」です.
つまり,目的関数を微分して,その微分結果に応じて内側の設計変数を更新していきます.
これだけです.
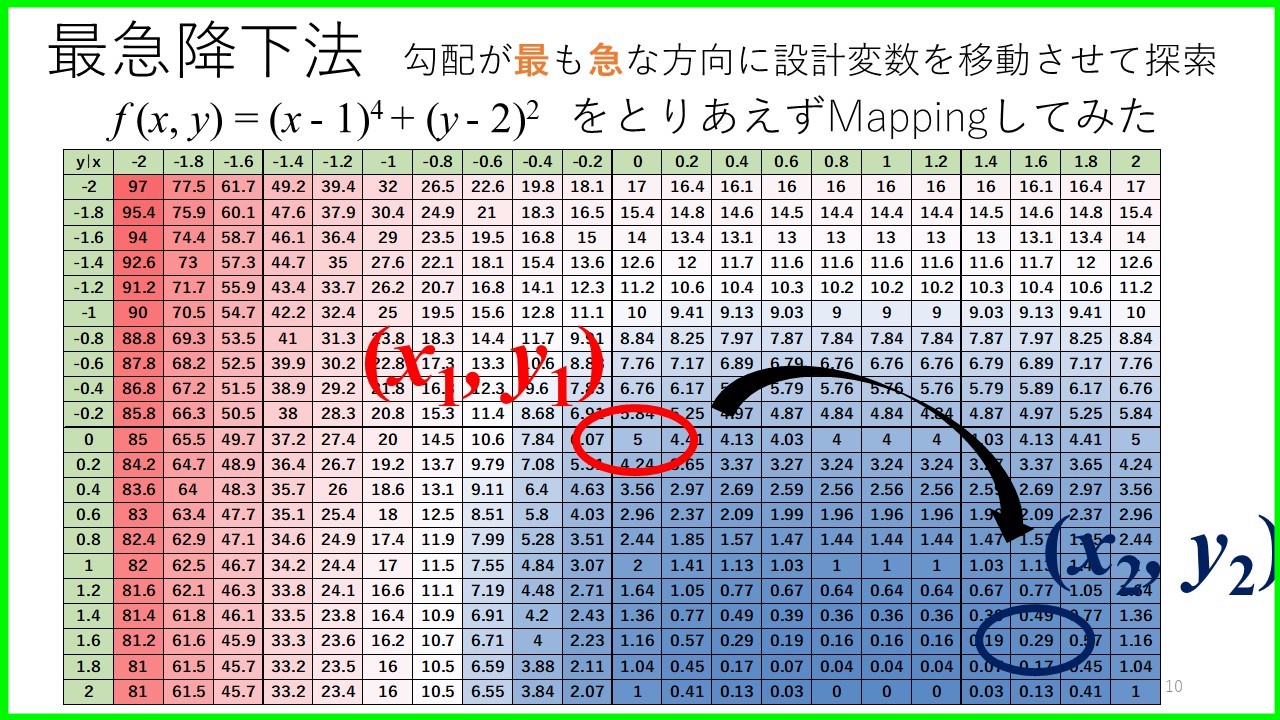
とりあえず,今回行う最急降下法の数値を各変数の0.2間隔ごとにプロットしていきましょう!

そうすると,上のような値が計算されます.
横軸は\(x\)で,縦軸は\(y\)の値です.
今回最適化問題(最小化問題)を解く際にあらかじめ各設計変数に値を入れて計算しています.
そうすることによって,どこらへんが目的関数が大きくて,どこらへんが目的関数が小さいかをざっと見ることができます.
最急降下法のアルゴリズム
最急降下法のアルゴリズムを示しておきます.
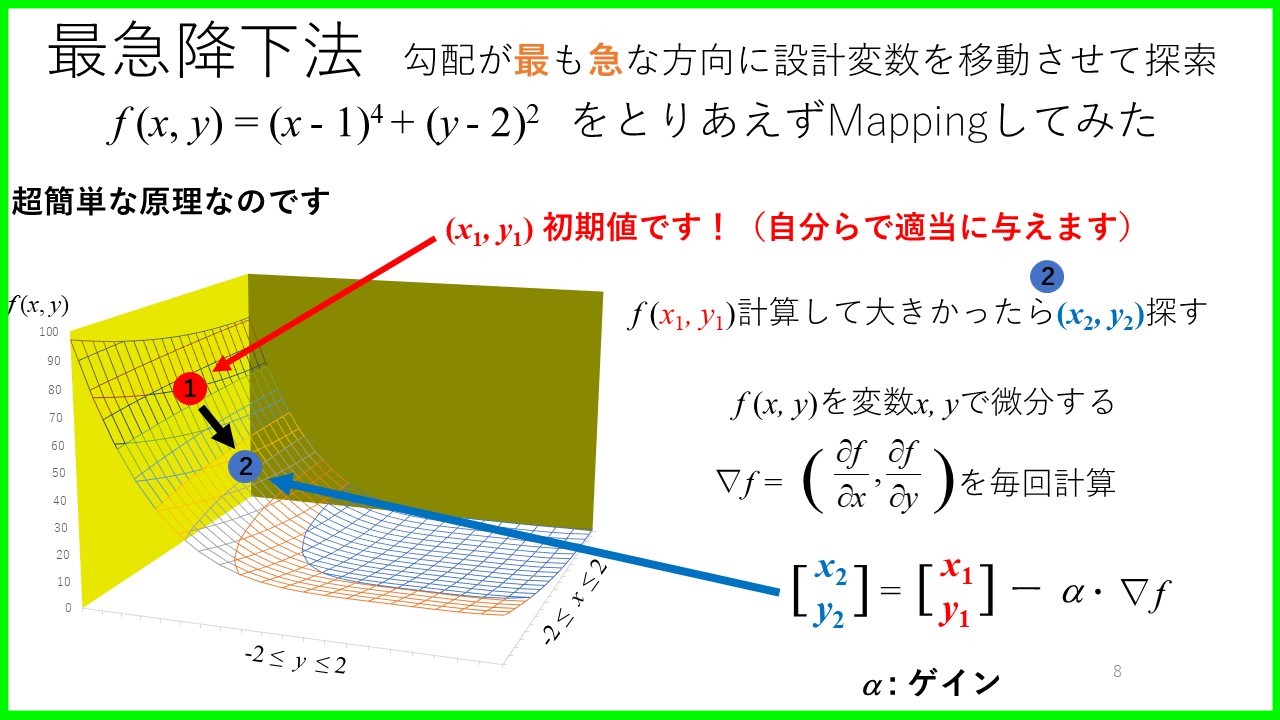
 設計変数の更新なんですが,目的関数を微分して,その勾配にそって更新していくだけの超簡単なものになります.
設計変数の更新なんですが,目的関数を微分して,その勾配にそって更新していくだけの超簡単なものになります.
とりあえず
- 初期値(\(x\),\(y\))→(0, 0)
- ゲイン0.4
の状態から回すと,次の更新された点は(1.6, 1.6)に移ることがわかりました.
これをただ繰り返し計算して,目的関数が最も設計変数を獲得できたら良いと思います.
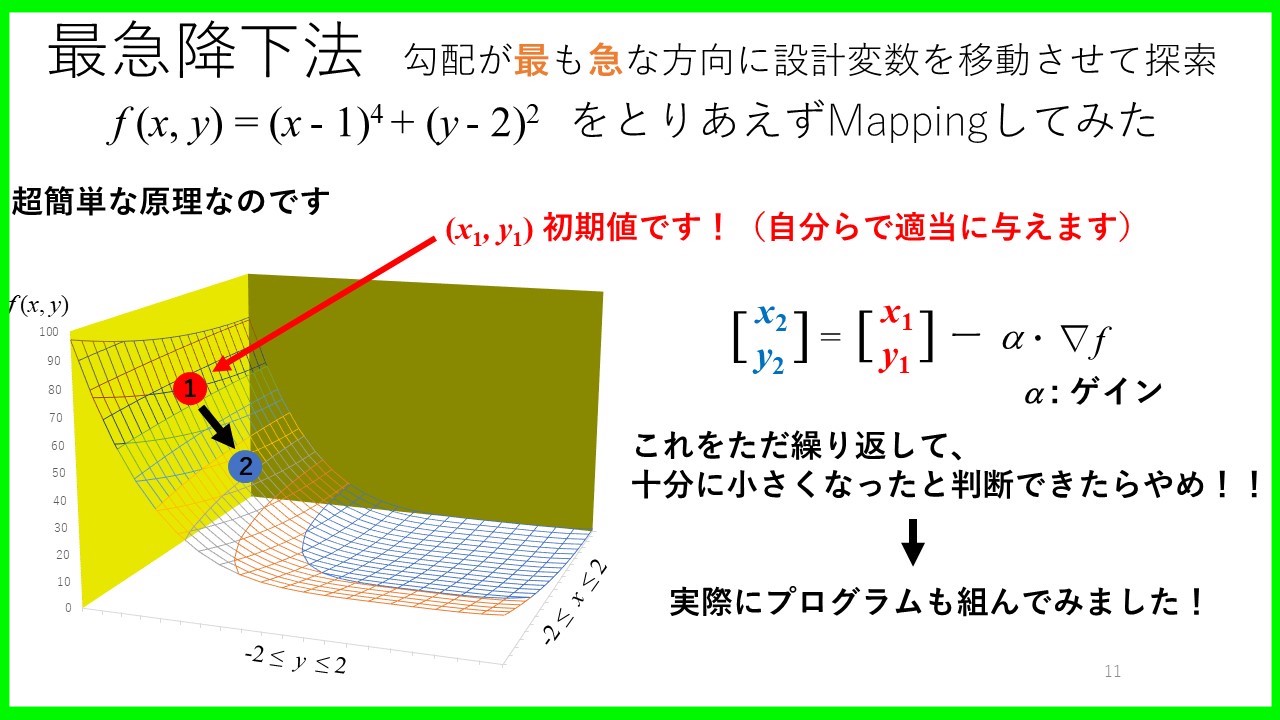
いちよう,プログラムを回してみると,適切な位置に落ち着くことがわかります.

プログラムに関して
今回回した解析プログラム(C++)も載せておきます.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 | /* 2017.8.3 uehara プログラム 最急降下法によって、関数の最小値を探索する。 f(x、y)=(x-1)^4+(y-2)^2 -2<x、y<2 df/dx = 4(x-1)^3 df/dy = 2(y-2) */ #include <stdio.h> #include <math.h> // 計算点座標 typedef struct pt{ double x; double y; }POINT; // f(x,y) double fz(double x,double y){ return pow(x-1,4)+4*pow(y-2,2); } // df/dx double fx(double x,double y){ return 4*pow(x-1,3); } // df/dy double fy(double x,double y){ return 2*(y-2); } void gridf(double xs[],double ys[]); POINT extreme(POINT p0,double xs[],double ys[]); int main(){ POINT p0;// x,y の初期値 POINT p; // x,y の極値点 double xs[]={-2.,2.};// 境界値 double ys[]={-2.,2.};// 境界値 gridf(xs,ys);// 予備調査:関数の分布 p0.x = 0.0;//初期値x p0.y = 0.0;//初期値y p = extreme(p0,xs,ys);// 最急降下法 //printf("extreme point is:\n"); //printf("at -\n"); printf("x = %.1f\n",p.x); printf("y = %.1f\n",p.y); //printf("results -\n"); //printf("f = %f\n",fz(p.x,p.y)); //printf("fx = %f\n",fx(p.x,p.y)); //printf("fy = %f\n",fy(p.x,p.y)); return 0; } void gridf(double xs[],double ys[]){ int i,j;//_格子点インデクス double x,y,z;//_格子点座標、関数値 printf("-2<=x,y<=2\n"); // printf("preliminary research of f(x,y)\n"); //printf("f(x,y)\n"); //for(i=0;i<=21;i++){//マッピング格子を表示する 5×5 // for(j=0;j<=21;j++){ // x = xs[0]+j*(xs[1]-xs[0])/21; // y = ys[0]+i*(ys[1]-ys[0])/21; // z = fz(x,y); // printf(" %6.0f",z); // } printf("\n"); //} printf("f(x,y)の勾配を確認するためのマップ。+ or -ともに大きい方が勾配がきつい\n"); printf("df(x,y)/dx\n"); for(i=0;i<=10;i++){ for(j=0;j<=10;j++){ x = xs[0]+j*(xs[1]-xs[0])/10; y = ys[0]+i*(ys[1]-ys[0])/10; z = fx(x,y); printf(" %6.0f",z); } printf("\n"); } printf("df(x,y)/dy\n"); for(i=0;i<=10;i++) { for(j=0;j<=10;j++) { x = xs[0]+j*(xs[1]-xs[0])/10; y = ys[0]+i*(ys[1]-ys[0])/10; z = fy(x,y); printf(" %6.0f",z); } printf("\n"); } return; } POINT extreme(POINT p0,double xs[],double ys[]){ double x,y;// 座標 double h,k;// 勾配 double alf=0.04;// α係数 double dx,dy;// 座標修正量 double err;// 勾配の絶対値 double eps=1.e-5;// 許容誤差 POINT p;// 計算点 int n=0;// 繰返し回数 int m=1000000;// 繰返し回数制限 //printf("\nexteme():\n"); //printf("execute Steepest descent method\n"); //printf("alf=%f, eps=%f, limit=%d\n",alf,eps,m); x = p0.x; y = p0.y; printf("初期値\t x0=%.1f, y0=%.1f\n",x,y); do { n++; h = fx(x,y); k = fy(x,y); dx = alf*h; dy = alf*k; x -= dx; y -= dy; //_領域境界制限(追加) if(x<xs[0])x =xs[0]; if(x>xs[1])x = xs[1]; if(y<ys[0])y = ys[0]; if(y>ys[1])y = ys[1]; err = fabs(h)+fabs(k); if(n>m){ //printf("%diteration, abort.\n",n); break; } //printf("%d_%f_%f_%f_%f\n",n,x,y,h,k); } while(err>eps); printf("イタレーション回数⇒%d \n",n); p.x = x; p.y = y; return p; } |
参考にした本はこちら
「工学のための最適化手法入門」