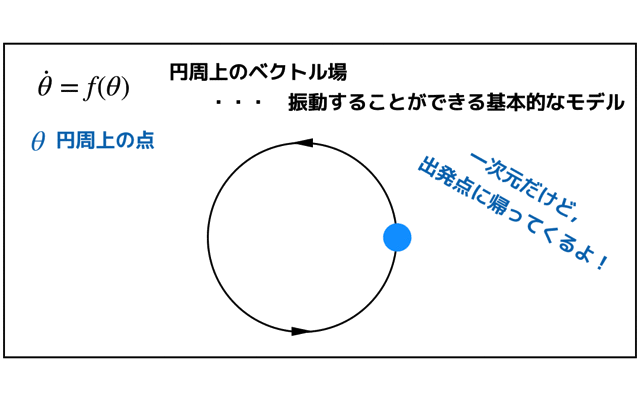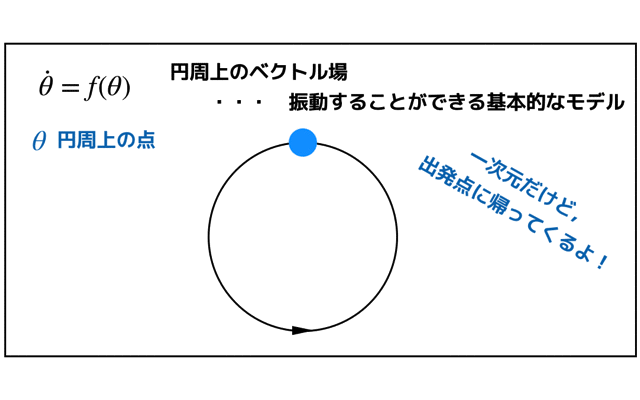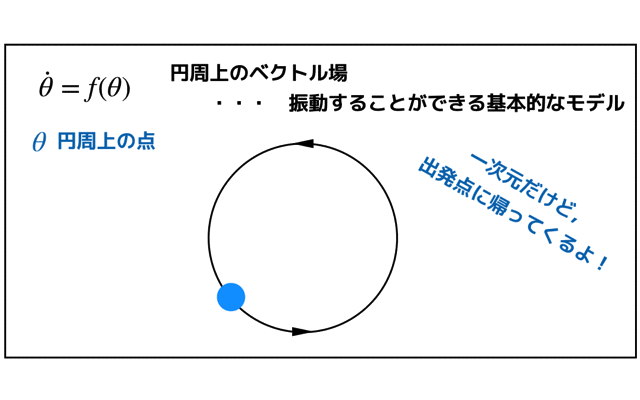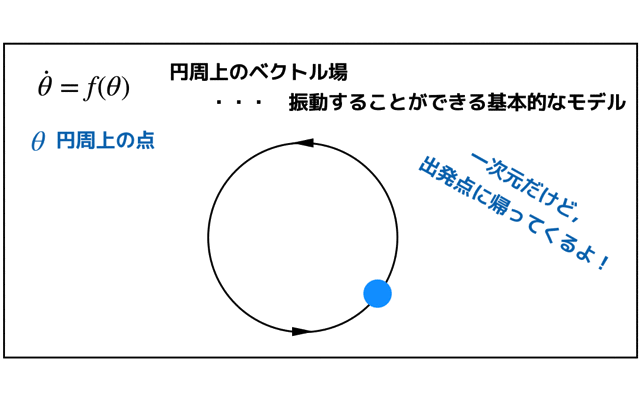
- 非線形ダイナミクスとカオスを一緒に勉強していきたい人
- 力学,物理学,数学が好きな人
- ロジスティック方程式が好きな人
こんにちは.けんゆー(@kenyu0501_)です.
今日もゆるい勉強会をやっていきます.
毎日ちょっとずつ本を読んで理解度を増やしていきましょう.
ということで,今回やるところは,第2章の「個体数の増加」ですね.
そういった個体数の増加を模した数学的モデル「ロジスティック方程式」について解説していきます.
気になる人はYoutubeに動画を上げているのでご覧ください.
また時間がない人は,この記事に動画のスクリーンショットを掲載しているので見ていって下さい.
動画解説はこちら

ゆるーくやっているのでお許しを
マルサス方程式とロジスティック方程式

今日は,生物個体数の増加モデルをやります.
$$\dot N = r N$$
$$\dot N = r(1-\frac{N}{K})N$$
以上二つを取り上げます.
上の式は,マルサスの方程式と呼ばれ,生物の増加が指数関数的に増加するといったモデルです.
この式ができた当時1798年は,人口増加が爆発的に起こっていた背景もあり,このような数式に従うものと考えられていました.
しかし,そのようなことは起こりえません.
どこかでブレーキがかかります.
生物の個体の数が増えすぎると,ご飯どうするの問題とか,住処(すみか)どうするの問題が出てきて,結局,与えられた環境に適した数になります.そのため,マルサスの方程式が改良され,ロジスティック方程式が生まれました.
ロジスティック方程式の環境収容力
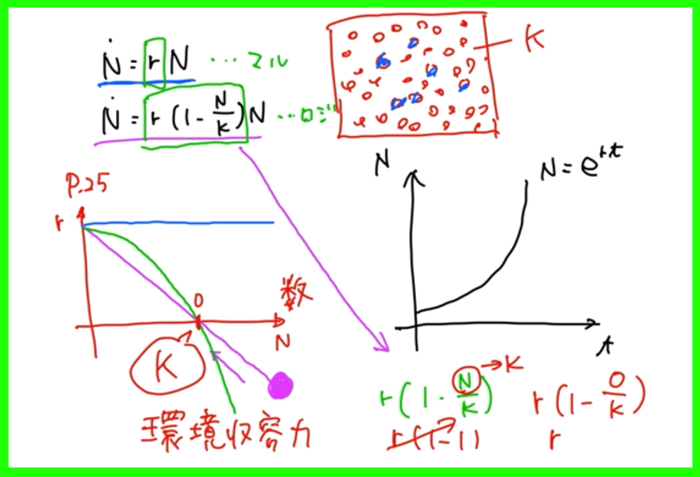
ロジスティック方程式は生物の個体数Nの増加をモデル化したものですが,このモデルは生物の個体数に応じて,増加率が変化していくものです.
個体数Nが増えれば増えるほど,増加率rは減少していきます.
ちょうどr=0となる点が,N=Kです.
ここで,Kは環境収容力になります.
ロジスティック方程式を幾何学的に解釈する
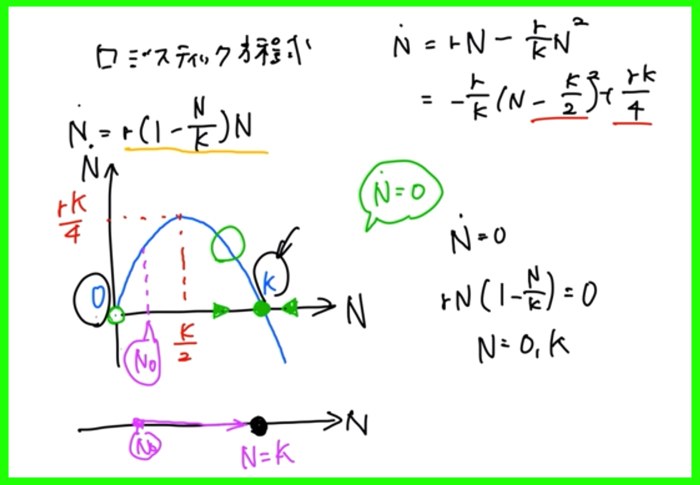
ロジスティック方程式を幾何学的に解釈します.
\(\dot N\)のベクトル場を書くことでした.
つまり解法としては,\(\dot N=0\)となる固定点を導出し,その周りの流れから固定点が安定か不安定を決めることでしたね.
\(\dot N=0\)となる固定点は\(N=0,K\)の二つです.
このうち,\(N=K\)が周囲のベクトルの流れから安定になります.
この解釈は,理論的に変数分離で問題を解いた場合と一致しますね.
生物の増加はシグモイドになる
もともとも個体の数が少ない時,例えばK/2よりも少ない時,生物の増加はシグモイドになります.
以下のようなS字曲線ですね.
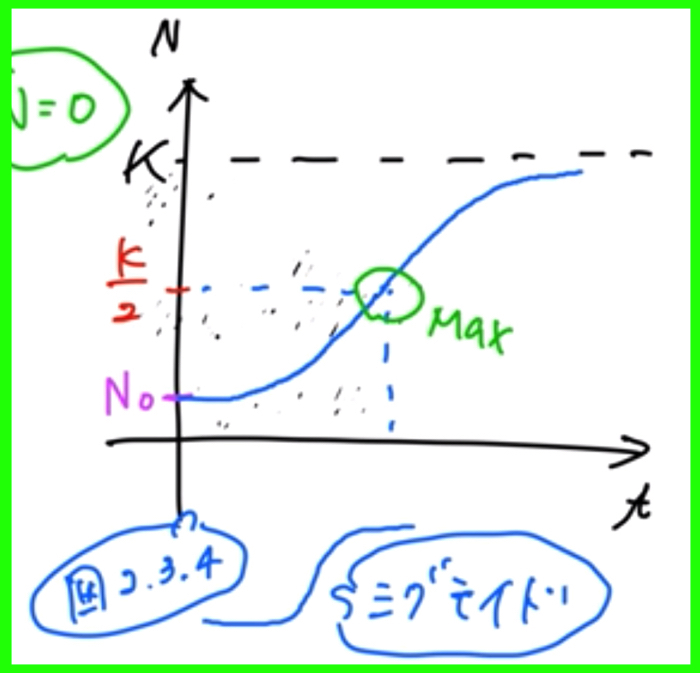
ロジスティック方程式はこのような値を吐き出すので凄いですよね.
生物の増加の仕方もきちんと模倣しているような感じがします.
基礎中の基礎ですけど,数学の神秘を感じますね.
終わり
[mathjax]