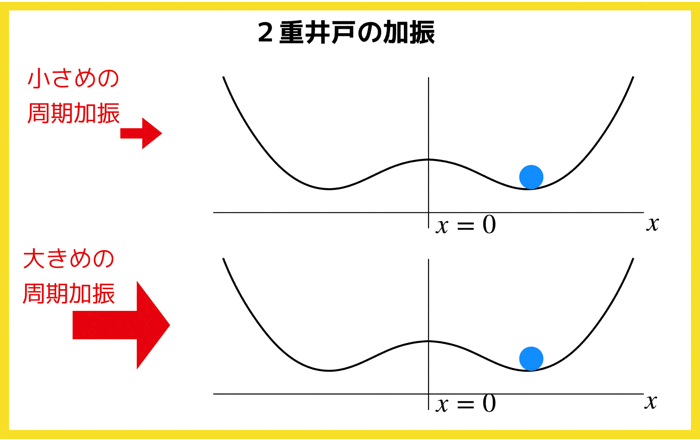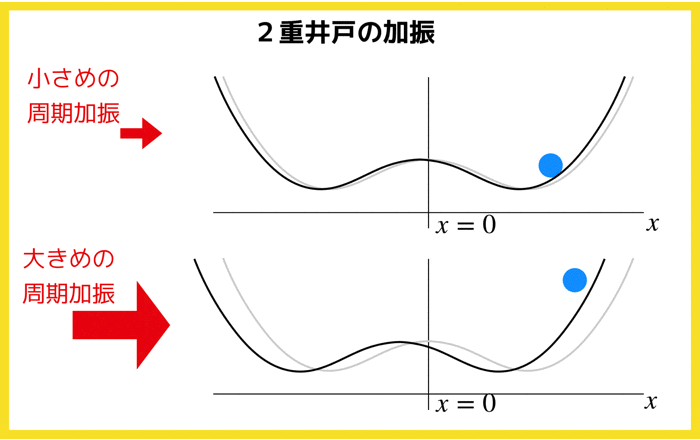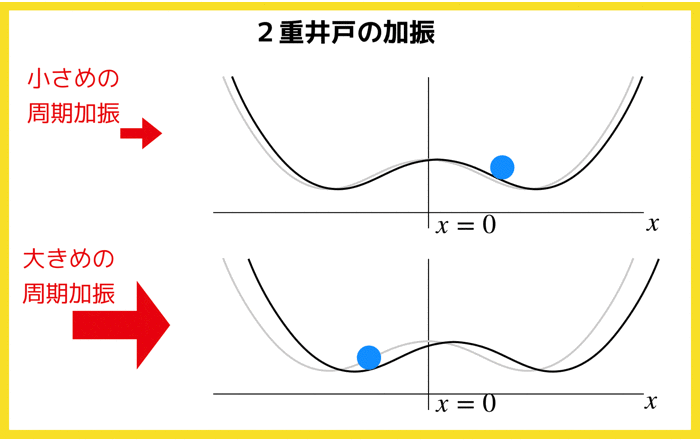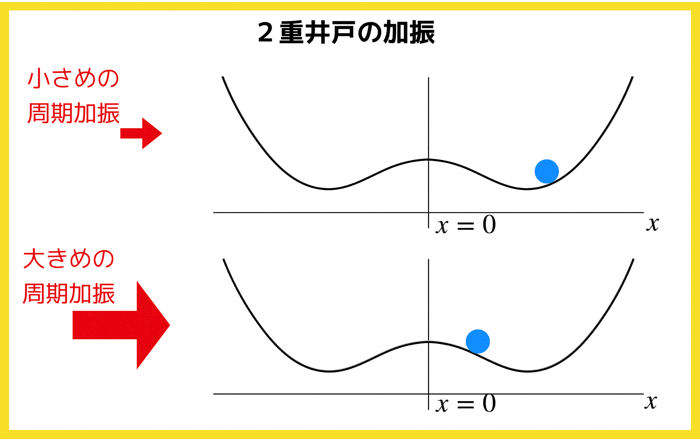
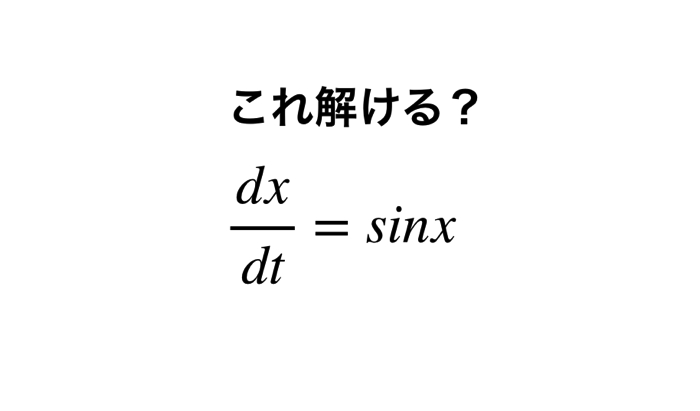- 「非線形ダイナミクスとカオス」を一緒に学習していきたい人
- 力学系を学んでいる全ての学生
- ベクトル的に非線形微分方程式の解き方を学びたい方
こんにちは.けんゆー(@kenyu0501_)です.
有名な著書である「非線形ダイナミクスとカオス」の勉強会をゆるーくやっています.
動画を見たいけど,そんな時間があんまりないという方に,こうやってブログでも進捗を残しておこうと思います.
Youtubeに書いた説明を貼るだけです.
動画解説はこちらです
今回やるところ
今回一緒にやるところは,第2章のp.19 – 20 (復習) ,p.20 – 24 ですね.
テキスト「非線形ダイナミクスとカオス」がある人は見てください.
無くても全然構いません.
そして,今日解く問題はこちらです.

それでは早速やっていきましょう.
前回の復習
復習の問題はこちらですね.
$$\dot x = \sin x$$
この問題は,以前詳しくまとめていたりもします
この記事はこんな人にオススメです 非線形系の解析に興味がある人 数学が好きな人 ストロガッツの非線形ダイナミク…
興味があれば読んでみてください.
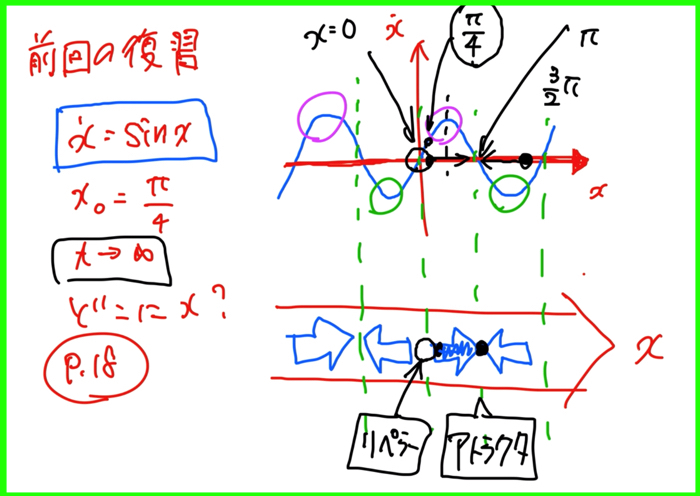
問題は,\(t\)→∞の解\(x\)の答えを求めるというものですが,相図を書くとすぐに答えが求まるのでしたね.
一次元\(x\)方向の流れ内に受ける流れの方向を考えて,仮想粒子\(x\)がどこに落ち着くかというものをみる問題でした.
安定固定点のアトラクタに行くので,答えは,\( \pi \)になります.
相図とは!?
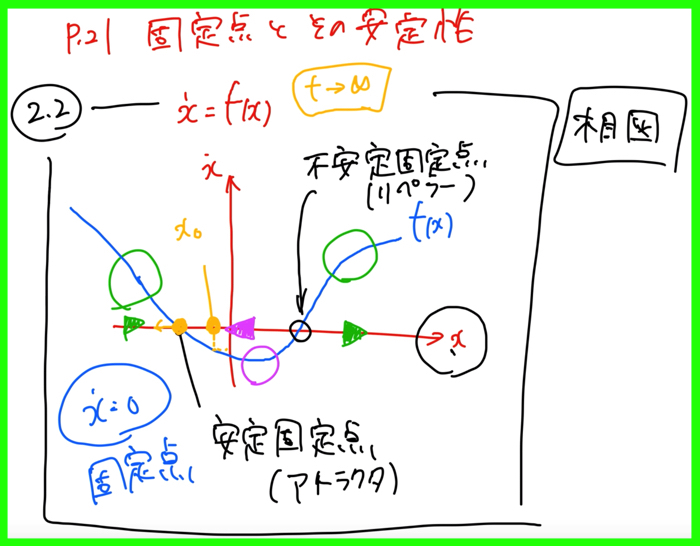
非線形微分方程式を解く場合には,従来の変数分離を解くものでも構いませんが,めんどくさいのですよね.
そこで,上の図のように,\(x\)と\(\dot x\)のベクトル場を考える幾何学的解法が便利であることを言いました.
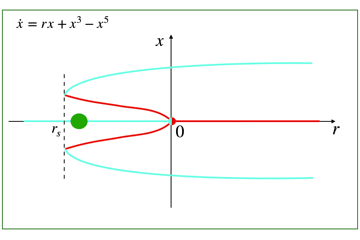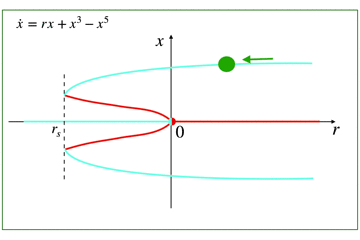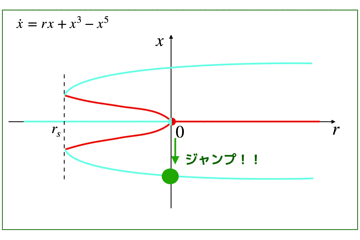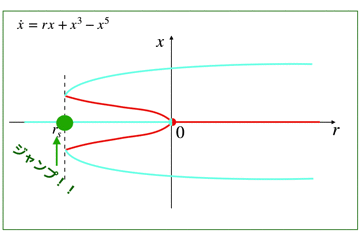
\(\dot x=0\)が固定点となりますが,その周囲の流れの向きによって,固定点が安定か不安定かが決まります.
安定固定点はアトラクタ,不安定固定点はリペラと呼びます.
\(\dot x=x^2-1\)を解く
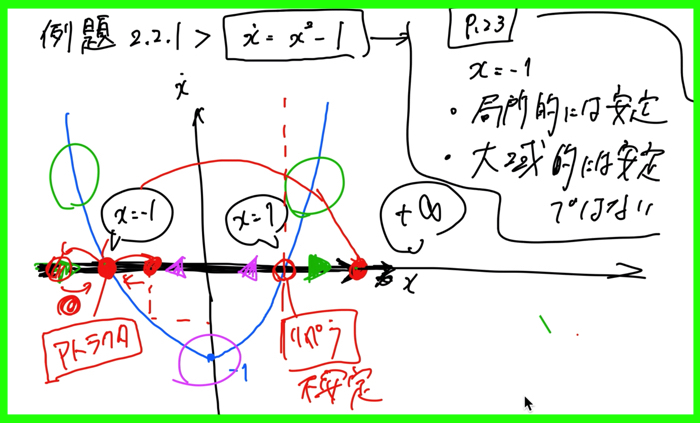
こちらの問題では,\(\dot x=0\)である固定点を探し,安定性の分類を行います.
\(x=1\)と\(x=-1\)が固定点となりますが,安定なのは,\(x=-1\)です.
しかし,大きな摂動があり\(x=1\)を飛び越えて右側に行くと,\(x\)が∞まで発散するので,大域的には安定ではないということになります.
\(\dot Q=-\frac{1}{RC}Q+\frac{V_0}{R}\)を解く
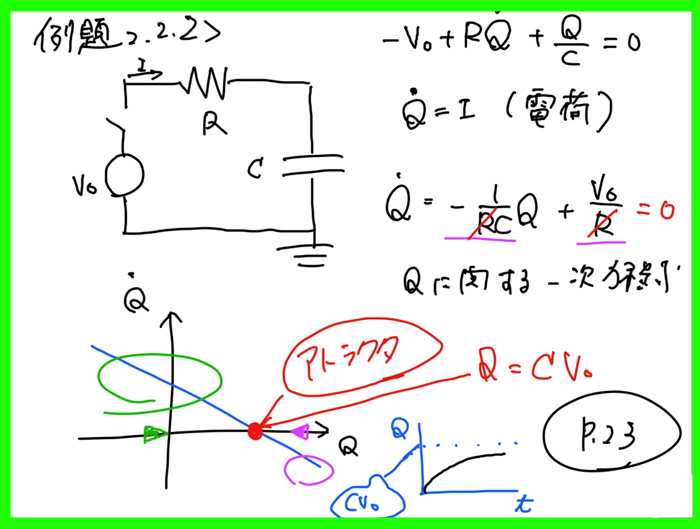
あまり電気回路が得意ではないのですが,系の安定を議論するためにこちらの問題も触れておきましょう.
今回も\(\dot Q=0\)の位置を探すのですが,今回はベクトル場が負の傾きを持つ一次直線になります.
この系だと,大域的にも安定になります.
\(\dot x=x-\cos x\)を解く
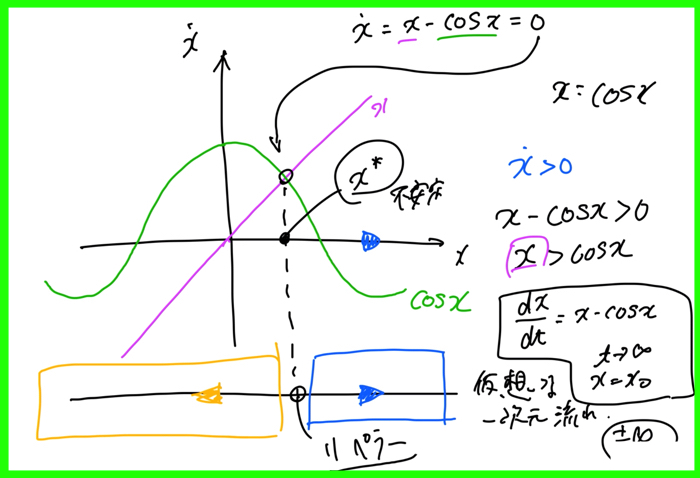
この場合は,ちょっとややこしいですが簡単です.
\(\dot x=0\)である固定点は\(x=\cos x\)になるので,その箇所を境に周囲の流れの向きを確認してください.
\(x>\cos x\)か,\(x<\cos x\)で流れの向きを計算します.
その結果,この場合の\(\dot x=0\)である固定点は不安定であることが分かりました.
リペラですね.
このような感じで非線形微分方程式を解いていきます.
次回はロジスティック方程式をやります.