- フーリエ変換について学びたい人
- 研究で周波数解析をしている人
- FFTなどを使用してはいるものの,フーリエ変換の内側のアルゴリズムを理解できていない人
こんにちは.けんゆー(@kenyu0501_)です.
前回の「複素フーリエ級数」に引き続き,今回は「フーリエ変換」についてやっていきます.
この記事はこんな人にオススメです. 複素フーリエ級数の理解を深めたい人 研究でフーリエ変換などを用いて周波数解…
(複素フーリエ級数に関してはこちら!)
複素フーリエ級数を理解している方は,フーリエ変換もかなり簡単に理解できると思います!
そして,ちょっと注意が必要なのは,このフーリエ変換は連続の関数\(f(t)\)を扱うものです.
(離散フーリエ変換とはまたちょっと違います.)

まずは複素フーリエ級数をちょっと復習して,連続フーリエ変換を学習するぞー!!それらの違いについてもはじめに比較していくよ!
複素フーリエ級数のおさらい
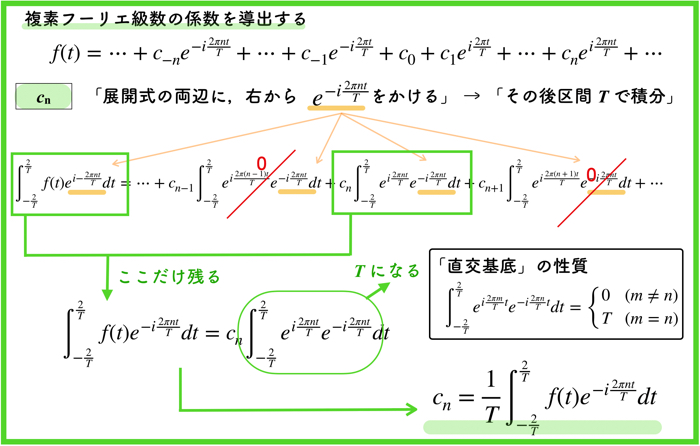
上のスライドは複素フーリエ級数展開の,フーリエ係数\(c_n\)を導出するものです.
このスライドをパッとみて,内容が理解できる方は,次に進んでください!
もし,内容が理解できないのであれば,こちらから複素フーリエ級数についてもう一度復習してみてください!
複素フーリエ級数とフーリエ変換の比較
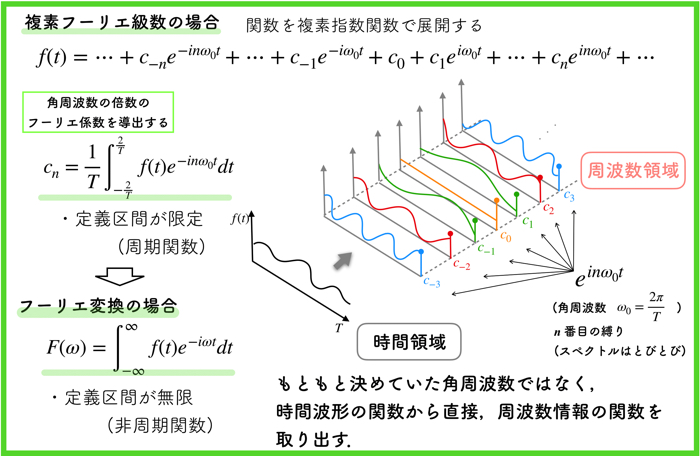
複素フーリエ級数の特徴
複素フーリエ級数は,関数を複素指数関数\(e\)で展開しましたね.
この複素フーリエ級数はいくつか大事なことがありました.
それは,
- 定義区間\(T\)が必要
- 周期関数を扱う
- 周波数スペクトルがとびとび
でしたね.
周期\(T\)で繰り返される波になるのでしたね.
またその結果,基本の角周波数\(\omega_0\)というものが出てきて,周波数情報は,その整数倍に従うものでした.
フーリエ変換は!?
一方でフーリエ変換はどうでしょう.
フーリエ変換は,複素指数関数\(e\)で展開するものの,関数\(f(t)\)の考える区間が無限です.
定義区間が\(T\)ではなく,-∞から∞なのです.
その結果,周期\(T\)で決められる基本角周波数\(\omega_0\)から算出される周波数スペクトル情報ではなく,連続関数になります.

複素フーリエ級数で計算される周波数は関数ではなく,「とびとびの値」だったね!基本角周波数\(\omega_0\)の整数倍だったね!
フーリエ変換は,以下のような特徴があります
- 定義区間が無限大
- 非周期関数を扱う
- 周波数スペクトルは連続関数になる!
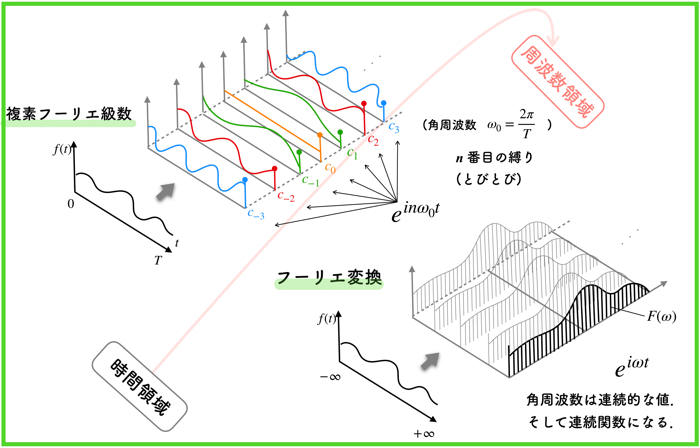
フーリエ変換では,周波数スペクトルが関数になることがとても重要なポイントです.
以下のイメージ図でざっくりと周波数情報の違いを理解してください.
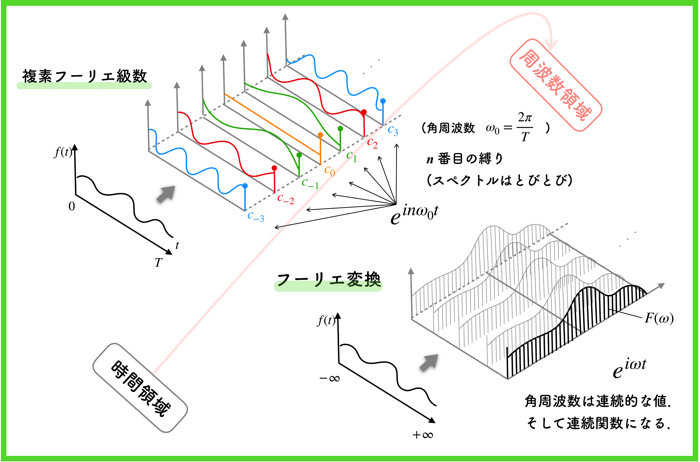

上のイメージが理解できると凄く良いぞ!
複素フーリエ級数からフーリエ変換への解釈

さてさて,「複素フーリエ級数」から「フーリエ変換」へ移り変わる解釈をしてみましょう!
級数展開の場合,周波数スペクトルが線で現れたと思います.
元の関数\(f(t)\)を表現するときには,無限に現れるそれらスペクトルの線の総和をとりました.
そうすることで表現してましたね!
フーリエ変換は,周波数成分がこのような線のスペクトルという考え方をしません.
ではどうやるのでしょうか.
フーリエ変換では,周波数成分を幅のもったブロックと解釈します.
周波数スペクトルが,最終的に連続になるのですが,これは考えている関数\(f(t)\)の周期\(T\)が無限大\(\infty\)であるからです.
角周波数は\(\omega_0=\frac{2\pi}{T}\)であるため,分母の大きさが無限大級に大きくなると,角周波数\(\omega_0\)は非常に小さくなるのです.
角周波数\(\omega_0\)が非常に小さくなった結果,周波数スペクトルの間隔が非常に狭くなり,線ではなくブロックで解釈するということになります.
そして,その一つ一つのブロックの面積を\(c_ne^{i\omega_0nt}\)と知れば良いのです.
これまで周波数情報を算出するために,周波数スペクトルの総和を計算する問題だったものに対して,フーリエ変換では面積を計算する問題となるのです.

面積を計算するから,積分が出てくるんだよ!区分求積分だね!
逆フーリエ変換の導出
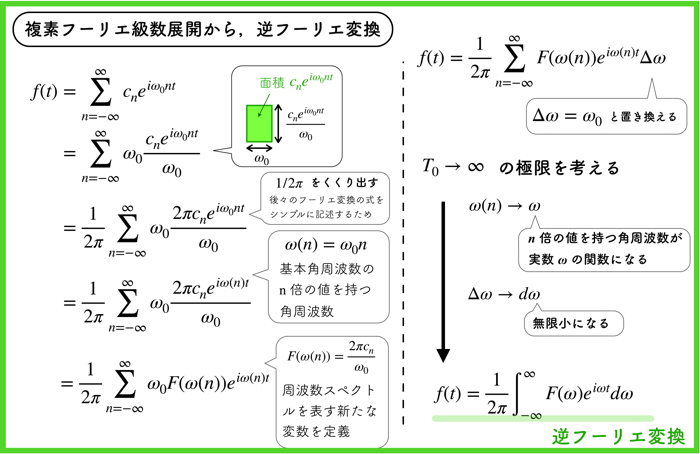
まず初めに逆フーリエ変換についての導出から行います.
なぜかと言うと,複素フーリエ級数展開に対応するのが,逆フーリエ変換だからです.
フーリエ変換の操作は,展開項のフーリエ係数を導出するものに対応してます.
では,上のスライドの複素フーリエ級数から逆フーリエ変換の式が導出される流れをみてください.
周波数スペクトルを面積として考える方法になります.
途中,\(\frac{1}{2\pi}\)でくくり出されているのは,フーリエ変換の式を簡単にするためです.
別にくくり出さなくても良いですが,その場合は,フーリエ変換の公式の前に\(\frac{1}{2\pi}\)が入ります.
(くくり出した場合は,逆フーリエ変換の公式の積分公式の前に\(\frac{1}{2\pi}\)が入っています)
式変形の際には,いくつか新しい変数も導入しています.
- \(\omega (n)=\omega_0n\)
- \(F(\omega (n))=\frac{2\pi c_n}{\omega_0}\)
\(\omega (n)\)は,基本角周波数\(\omega_0\)のn倍の値を持つ角周波数として定義してます.
\(F(\omega (n))\)は,周波数スペクトルを表す新たな変数です.
フーリエ係数\(c_n\)に関して色々と変化する値です.
それらを元に式を変形させて,最終的に\(T_0 → \infty\)の極限の状態を考えることによって,以下の積分の状態になります.
$$f(t)=\frac{1}{2\pi}\int_{-\infty}^\infty F(\omega) e^{i\omega t} d \omega$$
これが,逆フーリエ変換の公式になります.

ちょっと難しいけど,ノートに書き写しながら理解度を高めてね!
フーリエ変換の式の導出
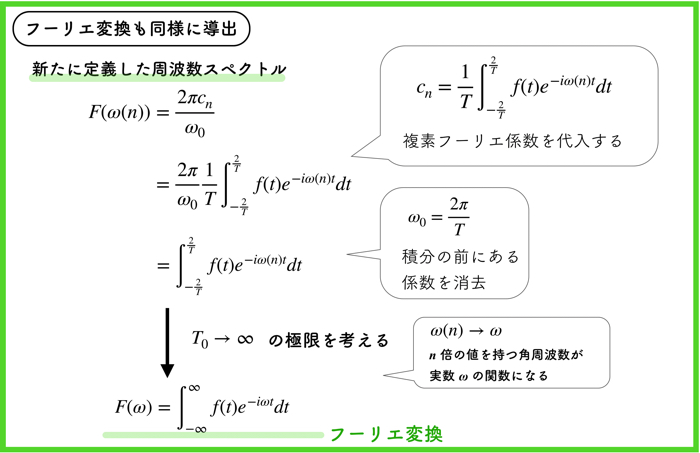
フーリエ変換の式の導出は,逆フーリエ変換で定義した新しい周波数スペクトルの式\(F(\omega (n))=\frac{2\pi c_n}{\omega_0}\)を使います.
この周波数スペクトルの式に含まれるフーリエ係数\(c_n\)に複素フーリエ係数の値を代入し,\(T_0 → \infty\)の極限の状態を考えることによって,以下の式を得ます.
$$F(\omega) = \int_{-\infty}^{\infty}f(t)e^{-i\omega t} dt $$
こちらがフーリエ変換の式になります.
(積分の前に\(\frac{1}{2\pi}\)が入っていないのは,逆フーリエ変換でくくり出していたからなのです)

フーリエ変換の公式がなぜそうなるのか理解できたかな!?
フーリエ級数展開と,フーリエ変換まとめ
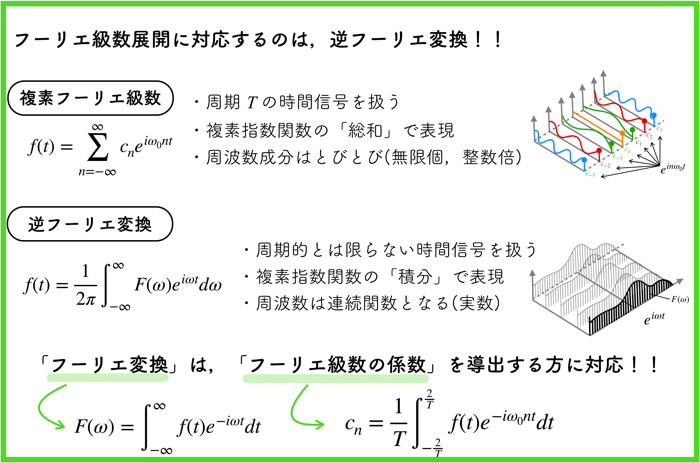
まとめておきます.
- 周期\(T\)の時間信号を扱う
- 複素指数関数\(e\)の「総和」で表現
- 周波数成分はとびとび(無限個,整数倍)
- 周期的とは限らない時間信号を扱う
- 複素指数関数\(e\)の「積分」で表現
- 周波数は連続関数となる(実数)
直交基底のお話


フーリエ変換は,時間の関数から周波数の関数に変換するものです.
関数から関数の変換なので,もちろん逆もできますよね.
フーリエ変換の場合は,時間関数に対して共役な複素数を右からかけて,-∞から∞までの積分を取るだけです.
また逆フーリエ変換は,その逆をすれば良いだけになります.
フーリエ変換も複素フーリエ級数と同様に,直交性の概念があるので,上の図で確認してください!
ここら辺の直交性の理解が十分でない方は,「関数の積の積分をとるということで内積=0とみなす理由」を覗いてみてください.
複素指数関数\(e^{i\omega_0nt}\)の,角周波数成分\(\omega_n\)がちょっとでも異なると,直交になります.
ここら辺は,複素フーリエ級数の理由と同じです.
(複素フーリエ級数を説明するブログへ)
動画解説

良ければ動画をみてくださいー!
練習問題:動画解説
道具としてのフーリエ解析という本を参考にしました.

動画解説です.
フーリエ解析まとめスライド

スライドにフーリエ解析の全てをまとめてあるぞ!80枚もあるぞ!
参考文献
参考にした本はこちらです.