- 離散フーリエ変換について詳しく知りたい人
- 高速フーリエ変換(FFT)を使用しているけど,内側の仕組みを詳しく理解できていない人
- 信号処理に興味がある人
こんにちは.けんゆー(@kenyu0501_)です.
今日は,「離散フーリエ変換(DFT)」について詳しくやっていきます.
前回は連続のフーリエ変換についてやりましたので,そちらを理解したい人は以下をご覧ください.
この記事はこんな人にオススメです フーリエ変換について学びたい人 研究で周波数解析をしている人 FFTなどを使…

複素フーリエ級数,連続フーリエ変換を理解しているのであればすぐに理解できるぞ!
離散フーリエ変換とは
離散フーリエ変換とは,離散データに関して行うフーリエ変換です.
フーリエ変換とは一般的に,時間領域のデータを周波数領域のデータに変換することです.
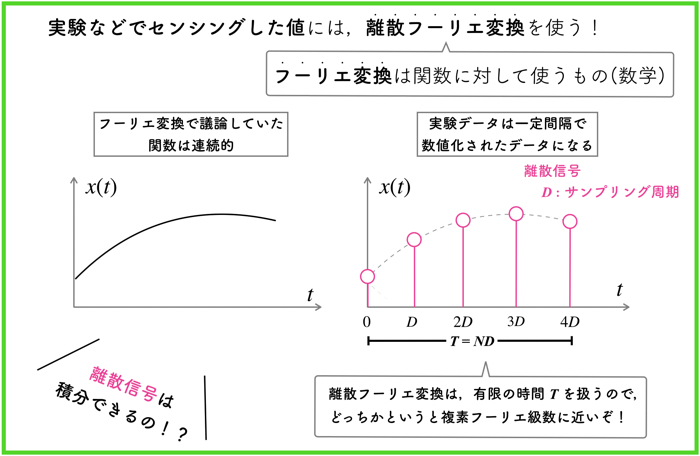
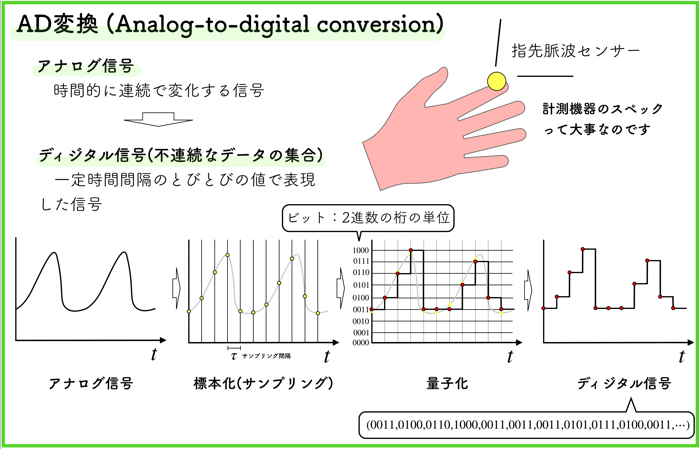
実験などでセンシングしたデータに関しては,飛び飛びの離散信号(ディジタル)になっているはずなので,そういったデータに関しては,離散フーリエ変換を扱います.
(アナログ信号からディジタル信号に変換するAD変換についてはこちらです.)
離散フーリエ変換は,有限の時間 \(T\) を扱うので,どっちかというと複素フーリエ級数に近いです.
前回やった連続のフーリエ変換は,-\(\infty\)から\(\infty\)までだったので,有限な区間という概念がありませんでしたね.
離散フーリエ変換は積分ができない
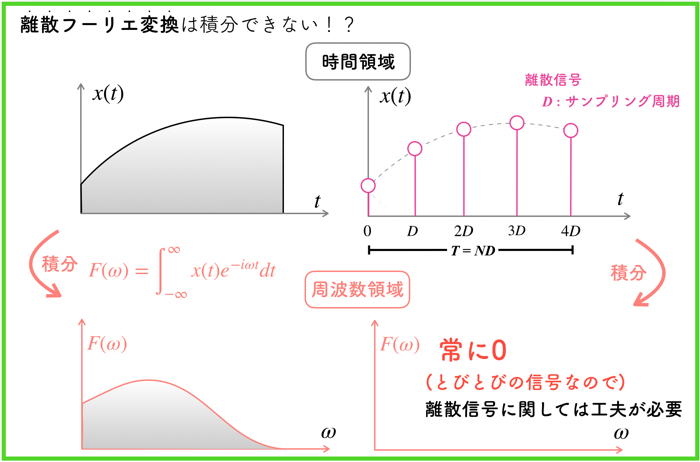
離散フーリエ変換は,ディジタル信号を扱っているので,積分ができません.
関数の面積という概念がないので当然っちゃ当然ですが,積分をすると0になります.
そのため,離散信号に関しては,ある工夫が必要です.
離散フーリエ変換で周波数領域に持っていく工夫
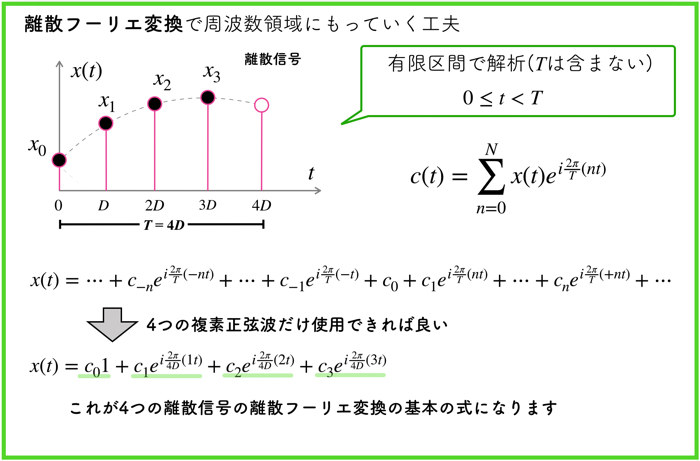
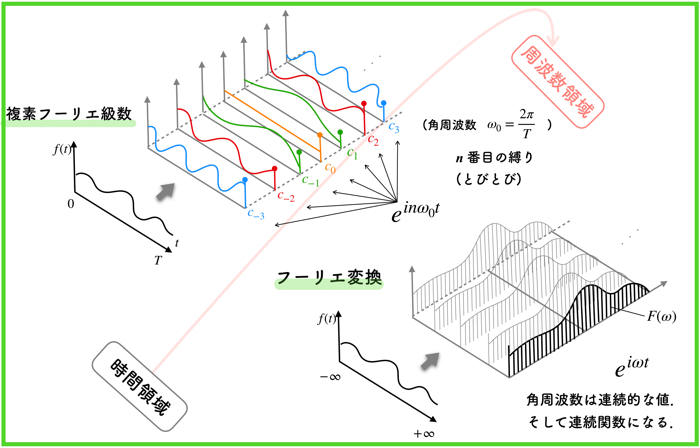
離散フーリエ変換では,複素フーリエ級数のように扱います.
上の図をご覧ください.
有限の時間 \(T\) に関して,それぞれの離散信号の数の分,複素正弦波に当てはめます.
上の例では,4つの信号があるので,4つの複素正弦波を使用しています.
こうして得られた式が,離散フーリエ変換の基本式になっています.
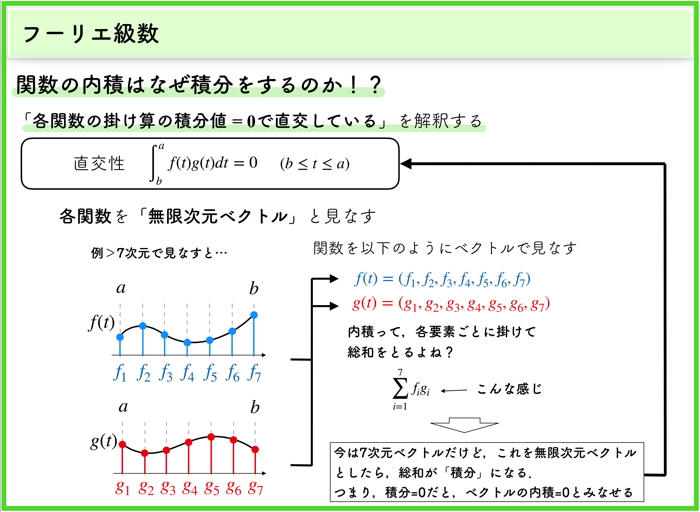
直交性に関して
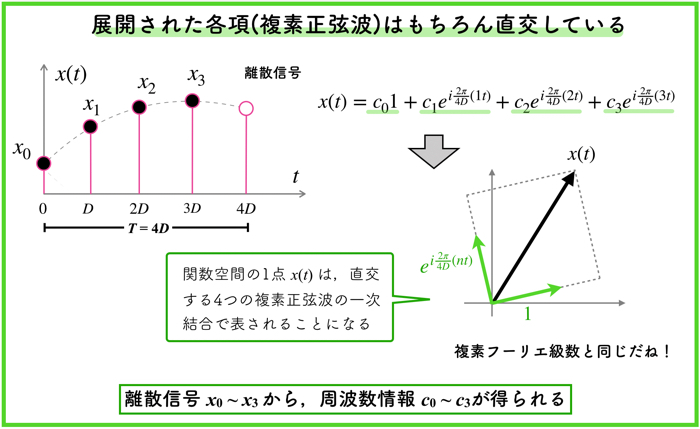
先ほどの例では,4つの複素正弦波を使用しましたが,それらは直交しています.
複素フーリエ級数と同じですね.
\(x(t)\) というものを関数空間の1点としてみたて,それを直交する4つの複素正弦波の1次結合として表したものになります.
この基本式に対して,各サンプル時間の値を代入していきます.以下をご覧ください.

以上の連立方程式を解いて,離散信号 \(x_0 ~ x_3\) から,周波数情報 \(c_0 ~ c_3\) の関係を導出していきます.
周波数情報の導出

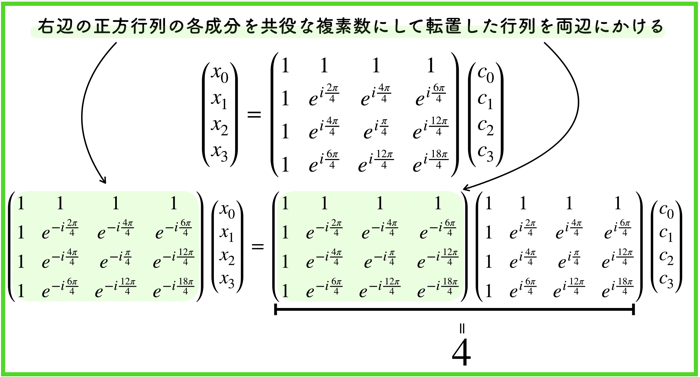
先ほどの4つの連立方程式を行列形式に変換します.
その後以下の操作を行って式の簡略化をします.
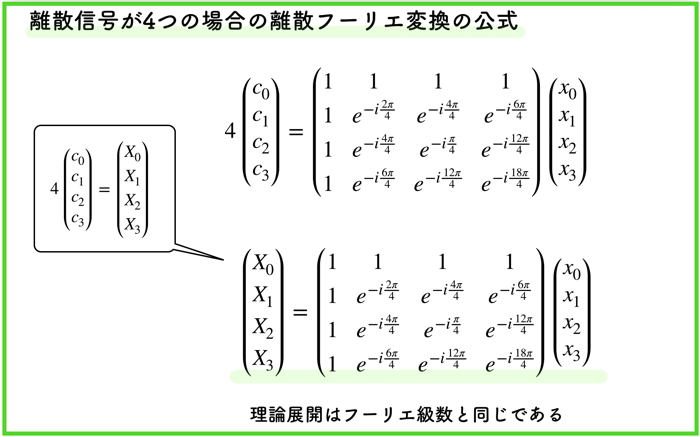

一般化したものが,上のものになります.
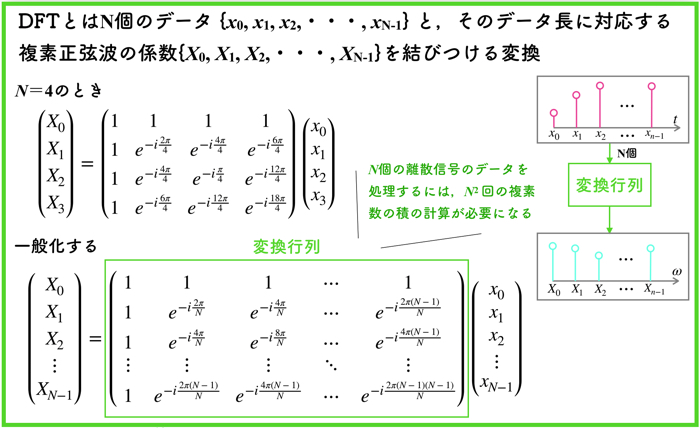
離散フーリエ変換とは, \(N\)個のディジタル信号 \({x_0, x_1, x_2, \cdots, x_{N-1}}\)と,そのデータ長に対応する複素正弦波の係数\({X_0, X_1, X_2, \cdots, X_{N-1}}\)を結びつける変換になります.
高速フーリエ変換への誘い
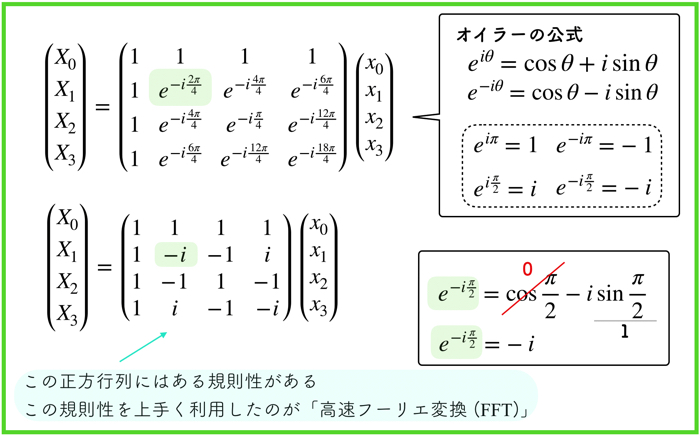
次回やりますが,高速フーリエ変換とは,変換行列である正方行列の規則性を上手く活用したものです.
逆離散フーリエ変換の導出
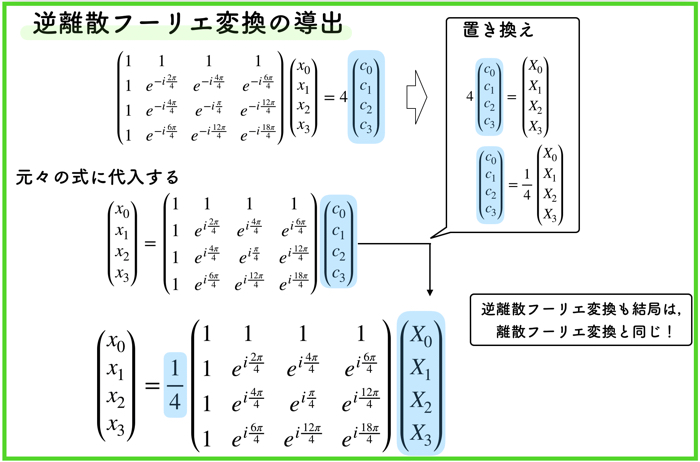
逆離散フーリエ変換も,離散フーリエ変換も結局は同じことですが,導出式(N=4の場合)を書いておきます.





非常にわかりやすいため、参照させていただいております。
さて、高速フーリエ変換への誘いの箇所でオイラーの公式がでてきますが、eiπは-1ではないでしょうか?