【フーリエ級数の直交性】関数の積の積分をとるということで内積=0と見なす理由

こんにちは．けんゆー（@kenyu0501_)です．
ここでは，フーリエ級数の直交性でしばしば出てくる「関数の積の積分=0」がなぜ「ベクトルの内積=0」に相当するのかということについて書いていきたいと思います．

とても簡単なんですぐに理解できると思うよ！

こちらのツイートに画像を貼ったので，サクッと理解したい人は，こちらの画像を見ていただけるとすぐに理解できると思います．

【フーリエ級数の直交性の話】
内積=0で直交しているは高校数学で習いますよね．

しかし，関数の積の積分=0は習いませんよね．
実は，そうなった場合も直交なのです．

フーリエ級数やフーリエ変換は，この直交性という概念が大事になるのです．

これ，ものすごく大切です！！！！！！！！！ pic.twitter.com/SGQejOwH3M

— けんゆー@博士課程 (@kenyu0501_) July 9, 2019

【フーリエ級数の直交性の話】

内積=0で直交しているは高校数学で習いますよね．

しかし，関数の積の積分=0は習いませんよね．
実は，そうなった場合も直交なのです．

フーリエ級数やフーリエ変換は，この直交性という概念が大事になるのです．

これ，ものすごく大切です！！！！！！！！！

画像に関しては，「無次元ベクトル」ではなく，「無限次元ベクトル」ですね．
(誤字です．すみません)
超多次元のベクトルがあると思ってください．

関数の直交性について

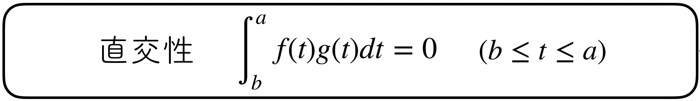
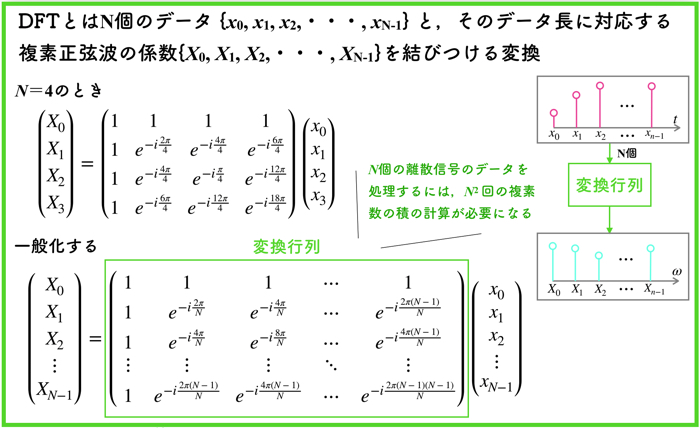
フーリエ級数や複素フーリエ級数でよく出てくるこの式，直交性を判断をするときの重要な式です．
ベクトルだと，内積を計算して0であれば直交していることになりますが，関数だとそうはいきません．
しかし，積の積分をとってそれが0であれば，二つの関数は直交していると言えます．

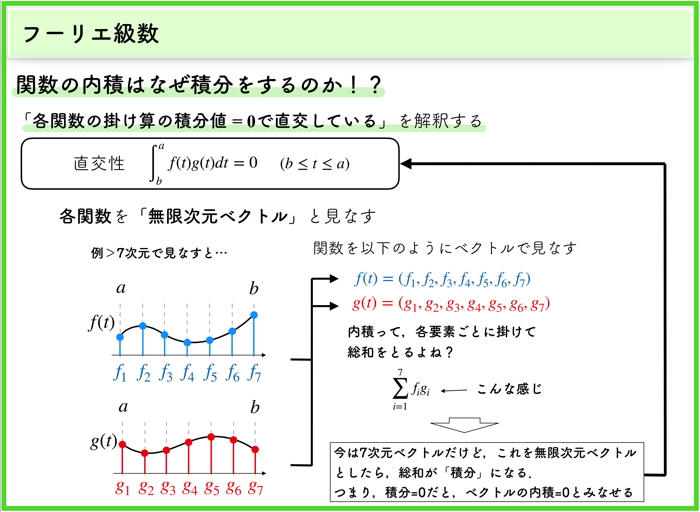
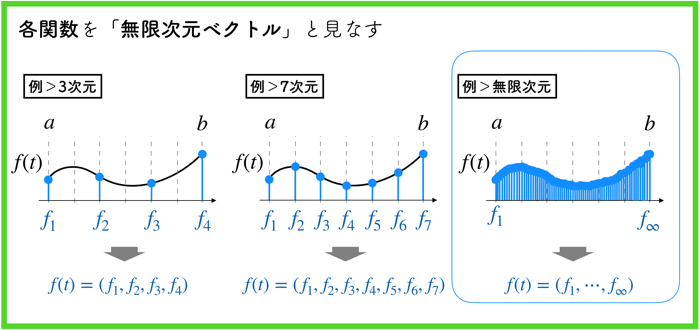
各関数を無次元ベクトルと理解できる

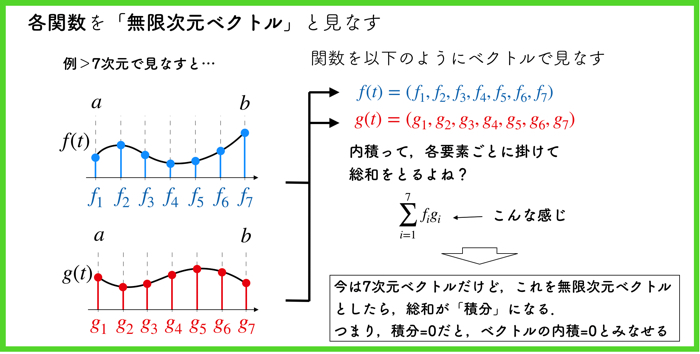
こちらの上の図でわりとサクッと理解できると思いますが，「関数」を「ベクトル」としてみなします．
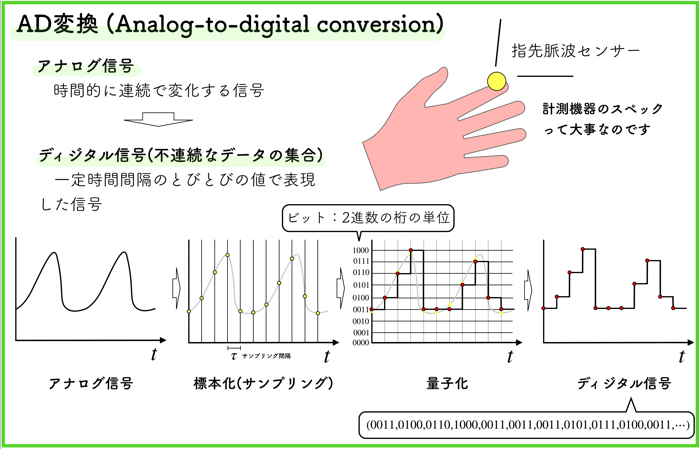
連続な関数をとりあえず，ある感覚でサンプルして，そのサンプルしたスカラー値の群をベクトルとして保持しておくわけですね．

ディジタル信号みたいだねー

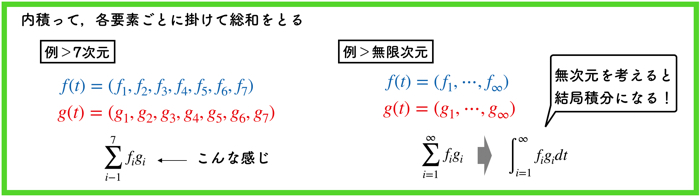
無限次元まで拡張すると，「シグマ(総和)をインテグラル(積分)とみなせる」わけです．
つまり積分=0だと，内積=0だとみなせるわけですね．

これでフーリエ級数のお話がすんなり理解できると思います．

「フーリエ級数」から「高速フーリエ変換」までのスライドはこちら