脳波解析：リアプノフ指数を計算して超簡単にカオスを測る！

この記事はこんな人にオススメです

脳波解析をしてみたい人
リアプノフ指数って何？ていう人
実際にプログラムを回してリアプノフ指数を算出してみたい人

こんにちは．けんゆーです（@kenyu0501_)
脳波を解析するための簡単な手法の一つである「リアプノフ指数」についてここでは触れて行きたいと思います．
実は，脳波というものはカオス的性質が認められている生体信号の一つです．

カオス性とは，また詳しく他の記事で触れていけたらと思いますが，簡単に記述すると，

「初期条件に依って後の経過が凄く影響される性質です」

つまり，はじめの小さい変化が，後になってとんでもない効果を及ぼす，，，といっておきましょうか．
一種のバタフライ効果みたいな感覚です．（蝶々の羽ばたきがハリケーンを起こす〜みたいな．）

さてさて，脳波もそのカオス性というものを保持しておりまして，このカオス性がどのくらい入っているのかを超簡単に調べる方法が「リアプノフ指数」を計算する方法です．

カオスを測るリアプノフ指数λとは

数学が不得意な人でもおそらく理解できると信じたい！式はこのようなものです！

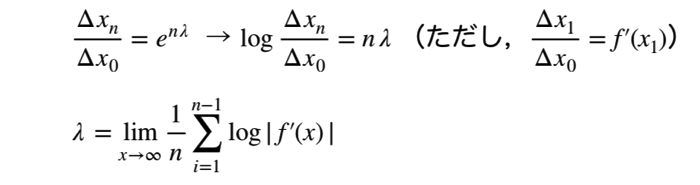
超簡単にリアプノフ指数を理解するために重要な式を2つだけに絞って持って来ました！

上の式について先に見ます．
上の式は，時系列波形の最初（初期値）の挙動の変化率△x_0と，n番目での変化率△x_nの比をeのnλ乗という形でとりあえず置いてます．このλがリアプノフ指数というものを表しています．

λ＞０の場合は，系の軌道xが無限大に離れていき（つまりカオス），λ＜０の時は軌道xは近づいていきます．
つまり，カオスというものは，系のリアプノフ指数λが正であれば良いのです（超簡単に説明しすぎてごめんなさい）．

初期の状態△x_0に対してn番目の状態△x_nがどの程度離れているのか？を示しているという事を言えばいいでしょうか．

とにかく，λが正であればn番目の挙動は最初の挙動に比べて指数関数的に離れていくので，「カオス」ということになります．

λの定義が分かれば，あとは計算するだけです．

２行目では，nの点数は十分大きいものだとして極限を計算しています．ちなみにf(x)の一階微分は，初期状態と次の状態の変化率を表します．

では，実際の脳波データとC言語によるプログラミングで計算していきましょう！！

リアプノフ指数を計算する

正直，波形データは脳波データではなくてもなんでも良いです！いろんなデータを調べてみても面白いと思います．おいらは脳波を研究しているので脳波データを使います！

実脳波データ

使用する時系列データ（脳波）はこちらです．

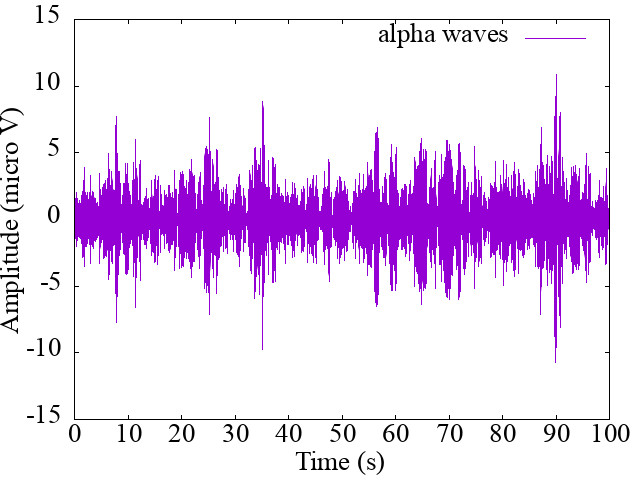
帯域制限を掛けてアルファ波（8-13Hz）のみを取り出しています．一応ヒト脳波データです．
こういう感じで実験しました！まあ，この辺は気にしなくてもいいです．

実験の条件

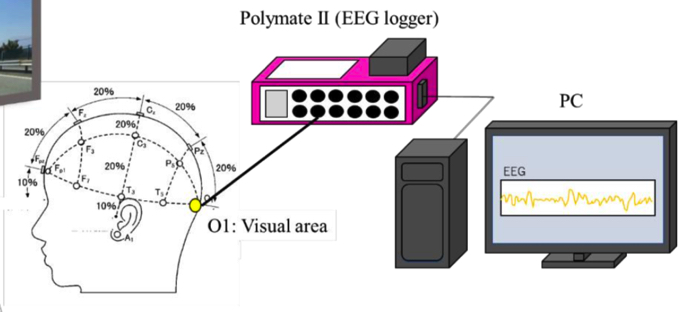
簡単に実験の条件だけ書いておきます．

後頭部の視覚野を計測．
風景画を観察している
１００秒間の脳波を計測
サンプリング時間は0.002秒
シールドルーム内で計測
前日にカフェインは取らない
脳波計はPolymate2

実験はこのような感じで行いました！しかし今回は，実験条件はどうでもいいです．

時系列データのリアプノフ指数を計算して，どのような値が出力されるのかがみたいので気にしないでください！笑

解析プログラム

C言語で解析プログラムの実装を行ってます！
簡単なプログラムですが転用してじゃんじゃん使ってもらって構いません！
主要な部分しか書いてませんので，mainを自身で書かれてください！

#define N 50000 // for 100 sec
#define Window 500 //analysis for 1 sec 
#define dt 0.002 //sampling time

//input data
if ((input = fopen("alphaWaves.txt","r")) == NULL){
	printf("Can't read your file 1\n");
}
for(int i=0; i<N; i++){
	fscanf(input," %lf\t %lf\n ",&t[i],&x_exp[i]);
}

//sum is lyapunov value
for(int e = 0 ; e<100 ; e++){
	sum = 0.0;
	for(int j=e*Window ; j<(e+1)*Window ; j++){		
		xdot[j] = (x_exp[j+1]-x_exp[j])/dt;
		sum = sum + log(abs(xdot[j]));	
	}		
	sum = sum/Window;
	printf("%d\t %.2lf\n",e,sum);
}

#define N 50000 // for 100 sec

#define Window 500 //analysis for 1 sec

#define dt 0.002 //sampling time

//input data

if ((input = fopen("alphaWaves.txt","r")) == NULL){

printf("Can't read your file 1\n");

}

for(int i=0; i<N; i++){

fscanf(input," %lf\t %lf\n ",&t[i],&x_exp[i]);

}

//sum is lyapunov value

for(int e = 0 ; e<100 ; e++){

sum = 0.0;

for(int j=e*Window ; j<(e+1)*Window ; j++){

xdot[j] = (x_exp[j+1]-x_exp[j])/dt;

sum = sum + log(abs(xdot[j]));

}

sum = sum/Window;

printf("%d\t %.2lf\n",e,sum);

}

簡単な流れだけ説明します．

実験データ(alphaWaves.txt)をx_exp[i]の配列に入れて行きます．
解析ウインドウ e（1秒）毎にリアプノフ指数sumを計算します．

sumについて
→これは，微分値xdot[i]の絶対値absの対数logを取り，足し合わせたものです．
→足し合わせたあと，windowのデータ数で割ります．

計算結果について

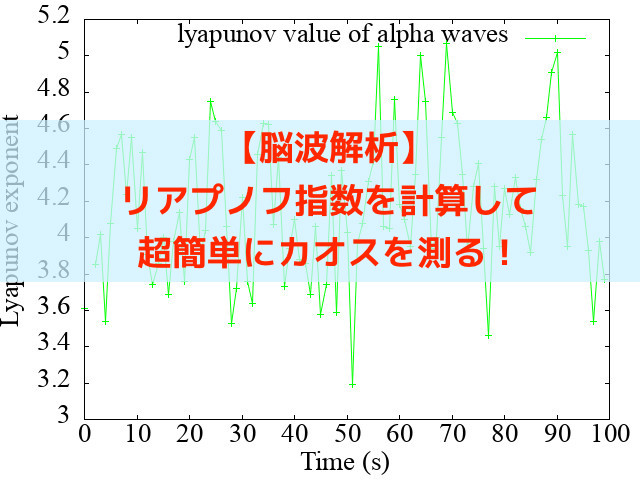
1秒ごとに算出したリアプノフ指数について示します

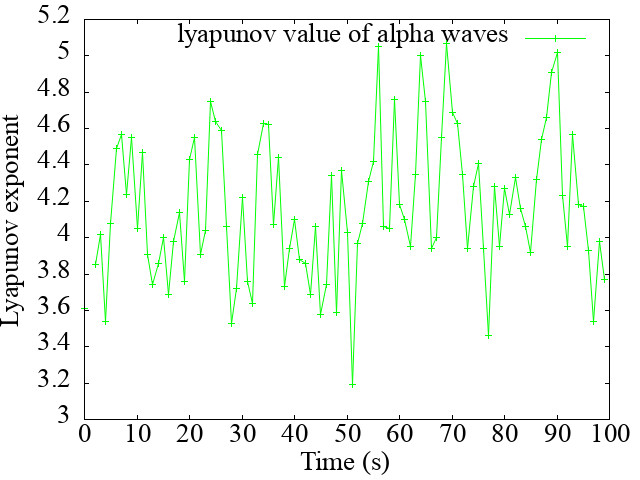
大体リアプノフ指数λが４程度の値を取っているのがわかりますね．
このようにして，様々な脳波に対してこのリアプノフ指数を算出することでカオス性がどのくらい入っているのかを調べることができたりします．

周期関数のサイン波ではどうなるの？

いちよう周期関数のsin(t)でも同様にリアプノフ指数λを計算しました．
sin(t)は，周期的な関数で全くカオスではないので，リアプノフ指数は正にはならないと予想できます．

では結果は，，，

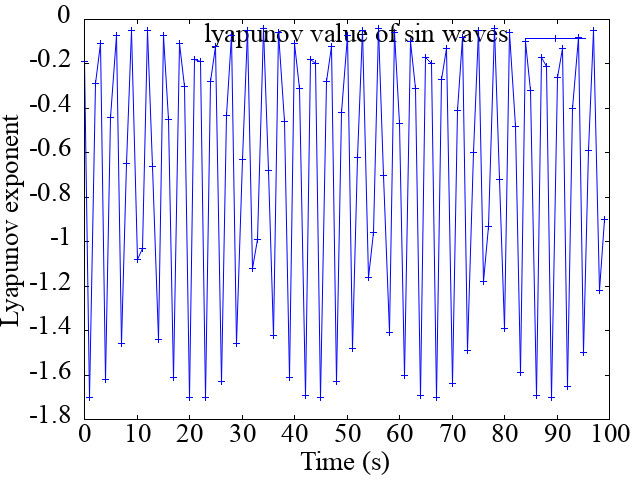
上の値は，サイン波sin(t)の１秒ごとのリアプノフ指数です．
全部の場合でリアプノフ指数がマイナスになっており，カオス性を持っていないことがわかりました．
また，カオス的な挙動を示すロジスティック写像やテント写像を使ってリアプノフ指数を計算しましたが，λ＝0.69となりカオス性があることを確認しています．