- Python初心者
- 数値計算で方程式の解を求めたい
- 2分法が知りたい
こんにちは.
Pythonで正の平方根を求めるには一般的に,
math.sqrt(x)
を使うとすぐに出てきますが,今回はわざわざ2分法というアルゴリズムで平方根を求めて見ることにします.
解説動画を出しました
2分法とは!?
2分法とは,解の存在範囲(上限値と下限値)を徐々に狭めていくことで求める方法です.
いちようスライドを用意しました!
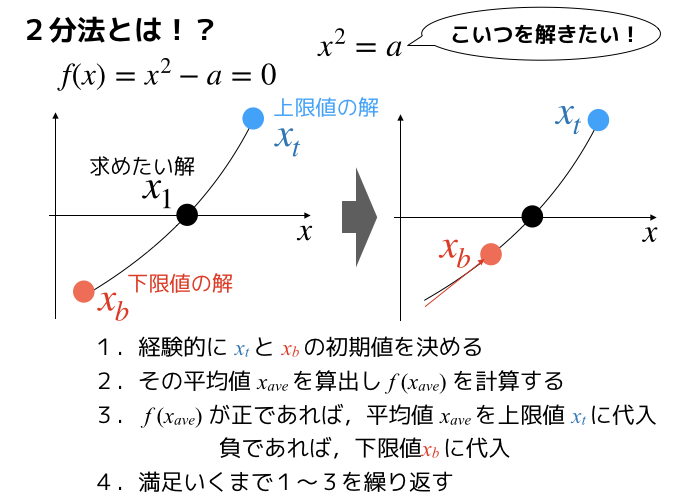
例えば,a=3だと,その平方根はだいたい1.732なので,上限値と下限値をだいたい3.0と1.0とかで推定します.
そのあとは,スライドのような計算を行って,徐々に上限値と下限値を解に近づけていけば完了です.
Pythonによるプログラミング
今回は,a=3の時で計算しました.
プログラムは以下の本を参考にしました.
(参考:Pythonによる数値計算とシミュレーション)
初期値として,上限値と下限値を最初に入れて,そのあとはその範囲を徐々に解に近づけて行きます.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | # -*- coding: utf-8 -*- a = 3 LIMIT = 1e-20 def f(x): return x * x - a xt = float(input("上限値xt=")) xb = float(input("下限値xb=")) while (xt - xb) * (xt - xb) > LIMIT: xmid = (xt + xb) / 2 if f(xmid) > 0: xt = xmid else: xb = xmid print("{:.15f} {:.15f}".format(xt, xb)) |
計算結果
上限値を3.0,下限値を1.0とした時の計算結果です.

左側の列が上限値,右側が下限値の計算結果になっています.
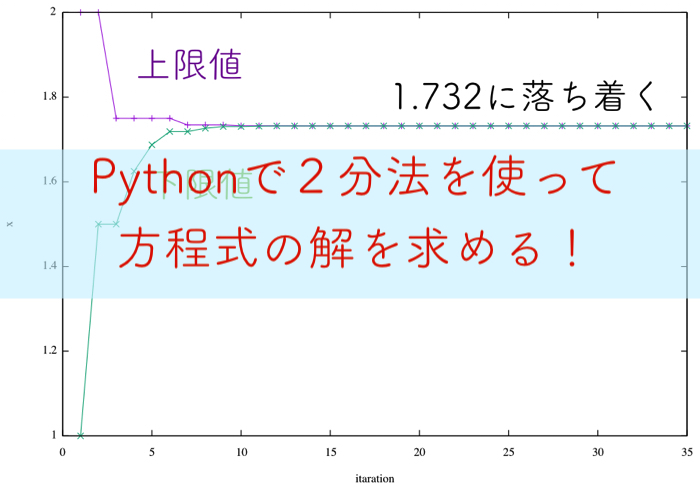
計算が繰り返されると,x=1.732になっていることが確認できます.

計算結果のグラフはこのような感じになります.
今回は,解を推定する方法として最も簡単な2分法を行いましたが,他にも色々な方法があるので,今後色々と取り上げて行きます.