- セルオートマトンについて詳しく知りたい人
- Pythonで数値計算をしたい人
- カオスやフラクタル的なことがちょっと好きな人
こんにちは.
今日はセルオートマトンについての記事を書きます.
実際に,セルオートマトンのプログラムを回して挙動を確認しているので,
この記事を理解できたらそこそこ「セルオートマトン」に関しては大丈夫なのではないでしょうか.
スライドも作ったので,もし見たい方がいたらご覧ください
ってか名前かっこいいですよね.
セルオートマトン!!!(厨二感出てますが,,,)
解説動画
セルオートマトンとは!?
セルオートマトンとは,ある内部状態をもったセルが,周囲の内部状態をもったセルと相互作用(情報交換)して時間的に変化していくモデルです.
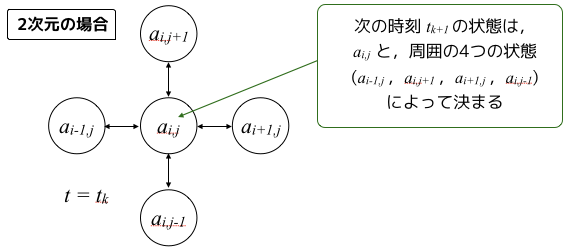
数理的にモデル化を行う上では,このような状態を考慮してモデルを組むと思います.
人間や生物の行動モデルにも使用される割とメジャーなモデル化です.
知っているとちょっといつか役に立つかもしれません.
数学的に言うと,一次元とか二次元とか色々ありますが,このように書けます.

セルの内部状態を更新する
各セルの内部状態を更新するアルゴリズムとしては,このような感じです.


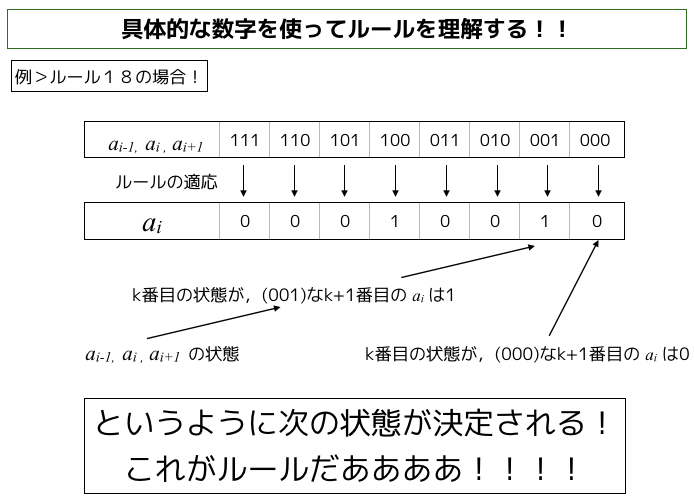

プログラムについて
スライドで説明した1次元のオートセルマトンに関してのプログラムです.
(参考:Pythonによる数値計算とシミュレーション)
詳しく内部構造を理解したい人は,上記の参考資料(Pythonによる数値計算とシミュレーション)をオススメです!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 | # -*- coding: utf-8 -*- import sys import numpy as np import matplotlib.pyplot as plt N = 256 R = 8 MAXT = 256 def setrule(rule,ruleno): for i in range(0, R): rule[i] = ruleno % 2 ruleno = ruleno // 2 for i in range(R - 1, -1, -1): print(rule[i]) def initca(ca): line = input("各Cellの初期値を入力:") print() for no in range(len(line)): ca[no] = int(line[no]) def putca(ca): for no in range(N - 1, -1, -1): print("{:1d}".format(ca[no]), end="") print() def nextt(ca,rule): nextca = [0 for i in range(N)] for i in range(1, N - 1): nextca[i] = rule[ca[i + 1] * 4 + ca[i] * 2 + ca[i - 1]] for i in range(N): ca[i] = nextca[i] outputdata = [[0 for i in range(N)] for j in range(MAXT + 1)] rule = [0 for i in range(R)] ruleno = int(input("ルールは??:")) if ruleno < 0 or ruleno > 255: print("ルールが正しくない(", ruleno, ")") sys.exit() setrule(rule, ruleno) ca = [0 for i in range(N)] initca(ca) putca(ca) for i in range(N): outputdata[0][i] = ca[i] for t in range(MAXT): nextt(ca, rule) putca(ca) for i in range(N): outputdata[t + 1][i] = ca[i] plt.imshow(outputdata) plt.show() |
プログラムの結果に関して
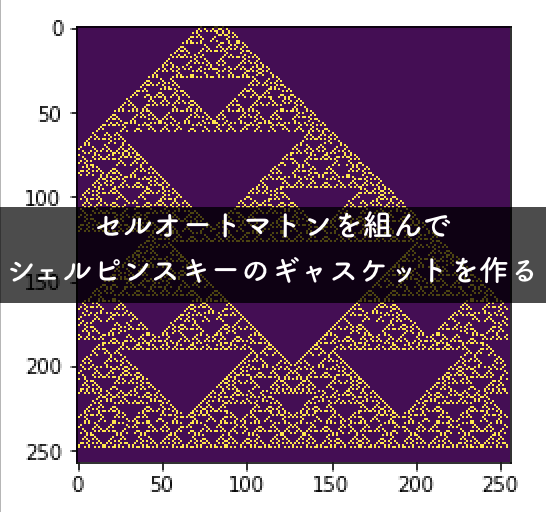
ルールを18で回してみました.

このような感じになりました!
内側のルールが同様なので,どのような初期値から演算してもこのような形になります.
シェルピンスキーのギャスケットですね!!!笑
また,インターネットを見ると,ルール161で,シェルピンスキーのギャスケットが見られると言うことで実際に試してみました!
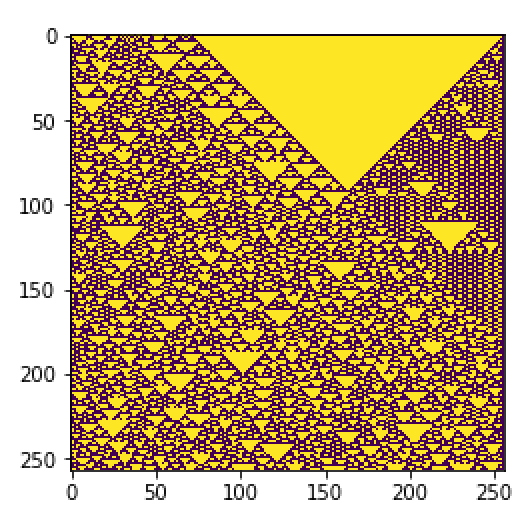
このようになりました笑
確かにところどころ,シェルピンスキーのギャスケットが見られる!
ちなみに,シェルピンスキーのギャスケットとは,フラクタル図形の一種です.
カオスがチラ見してますね
詳しくは,こちらのwikiを参考にして見てください!
(参考:シェルピンスキーのギャスケット)

以上の絵も,wikiから抜粋したシェルピンスキーのギャスケットです.
拡大しても拡大しても同じような絵が出てきますね!
数学の美を感じます!
では!