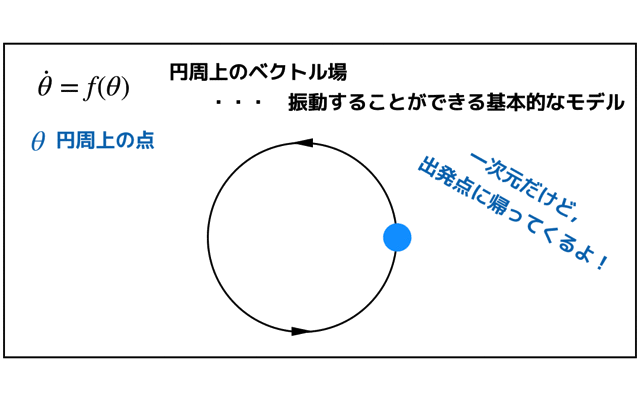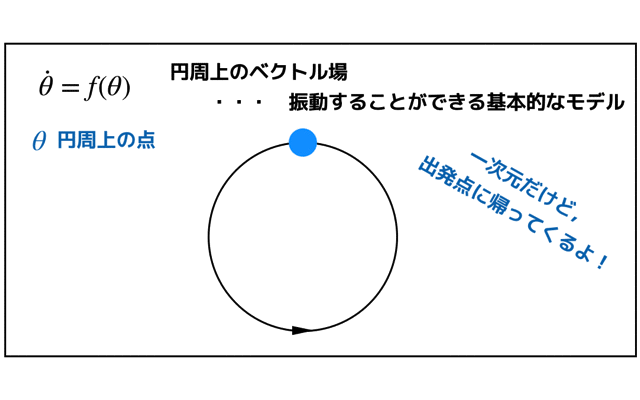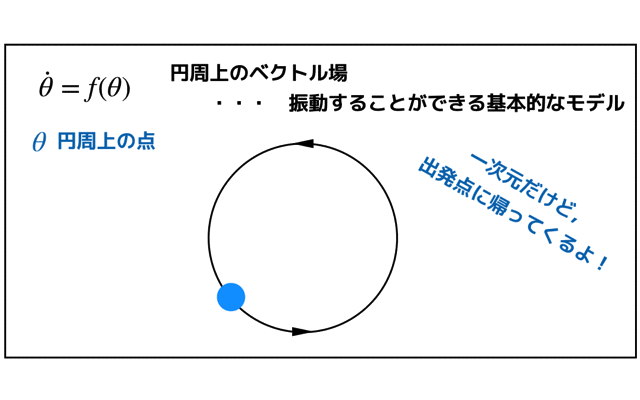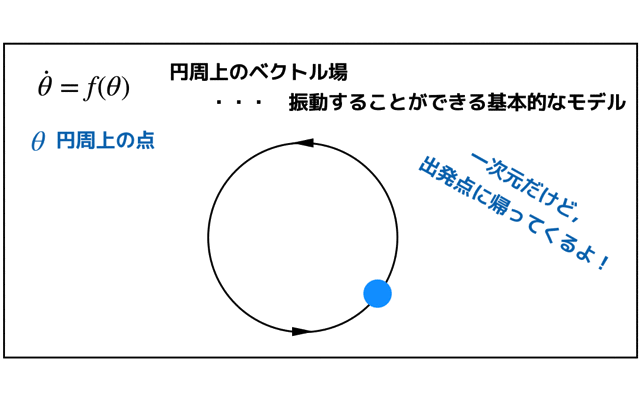
- 工学や数学で何かしらの数学的モデルを扱っている人
- ダイナミクスな系を考えるのが好きな人
- 分岐について知りたい人
こんにちは．以前，非線形微分方程式の解を幾何学的に算出するという記事を書きました．
そこでは，非線形微分方程式の解をベクトル場という図的理解によって解釈するということを書きました．
参考にした本はこちら．
今回も，上記の素晴らしい本を参考に記事を書きます．
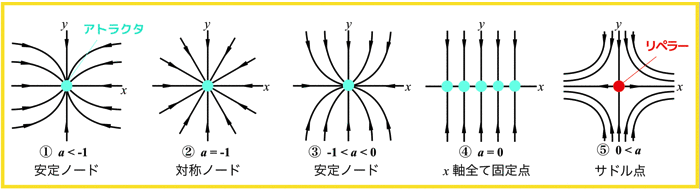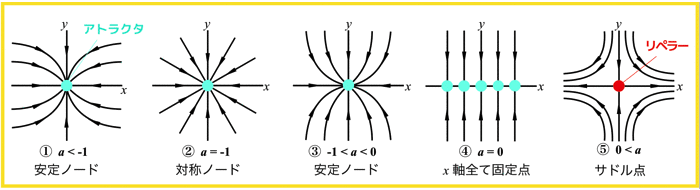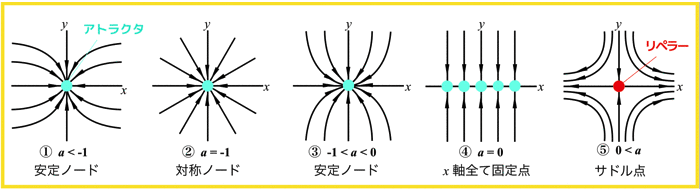
前回の記事の内容によると，直線上のベクトル場の定めるダイナミクスは，どうやら４種類の解しかないらしい．．
- 安定な固定点（アトラクタ）
- 不安定な固定点（リペラー）
- 正に発散
- 負に発散
ぶっちゃけていうと，2．の不安定な固定点（リペラー）に留まる場合は，与えられた初期位置がもともとそこのリペラーにいる条件のみで，ダイナミクスでもなんでもない（と言ったら数学者から袋叩きに会うので）宝くじが当たったような（代わりにちょっとポジティブな例えで．．）すごく現実的に可能性の極小なものですよね．
３と4の，正に発散も負に発散も，発散は発散なので，語弊を恐れず一括りに発散としましょう．
そうなると，ベクトル場の定めるダイナミクスって，正直，安定な固定点（アトラクタ）とそれ以外の安定ではない所なのですよ．
では，これの何が楽しいのよ！？
ってなりますが，内側のパラメータに依存して安定な固定点がちょこまか変化するっていうのはまぁ面白いわけですよ．
また，ダイナミクスの安定性の定性的変化は”分岐”と呼ばれてますが，今日は分岐の種類のお話です．
３種類の分岐を取り上げます．
「サドルノード分岐」，「トランスクリティカル分岐」，「ピッチフォーク分岐」です．
サドルノード分岐
サドルノード分岐は，最も基本的な分岐です．
パラメータの値によって固定点が出てきたり，消えたりする分岐です．
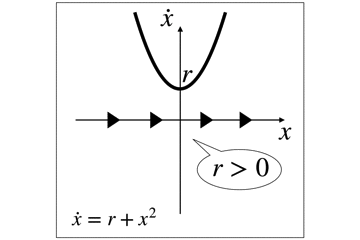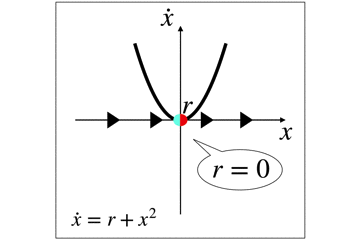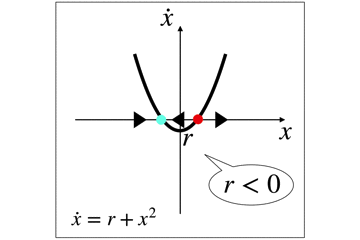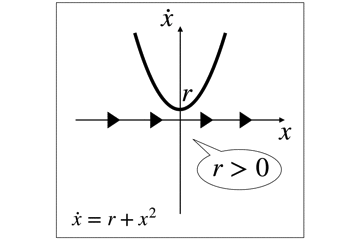
ここでの分岐に寄与するパラメータはrです．
rが負の時，2つの固定点が発生します
１つは安定（青）でもう１つは不安定（赤）です．
r＝0のとき，これらの固定点は１つになって，半安定な固定点（青と赤）となります．
以下は分岐図といいます．
分岐を図示する場合には，今回議論しているパラメータrが独立変数なため，普通はrを横軸にします．
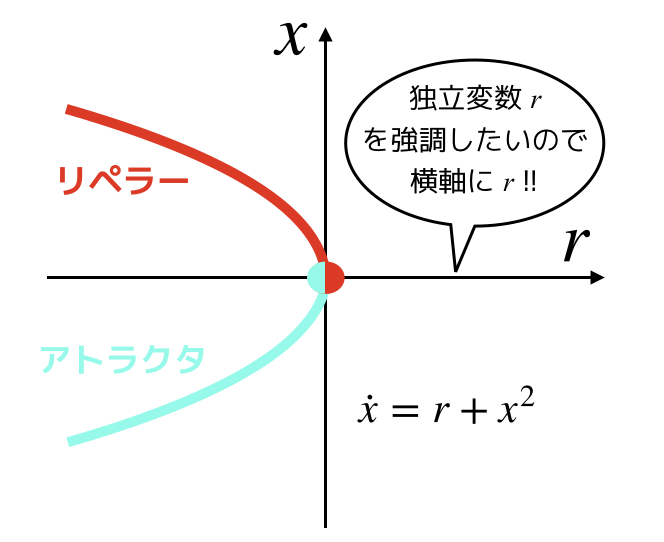
また，サドルノード分岐は，よくフォールド分岐や，ターニング分岐，さらにはブルースカイ分岐などとも言われたりもしますが，全部一緒です．
他のいろんな分岐についても見て行きましょう
トランスクリティカル分岐
トランスクリティカル分岐は，パラメータ依存により安定性の変化を示すものです．
サドルノード分岐は，安定性の発生と消失でしたね．
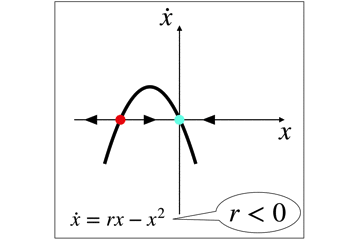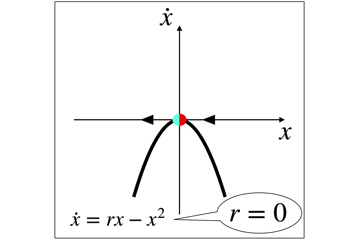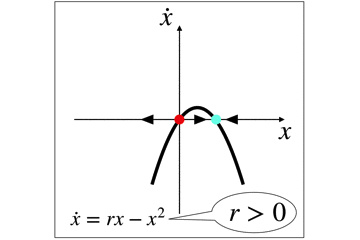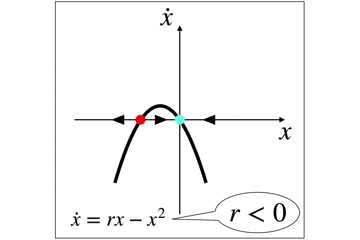パラメータによって安定固定点が発生・発生をする系もありますが，このように，安定点の場所が変化する分岐もあります．
パラメータのとりうる値全てに対して固定点がある場合ですね．
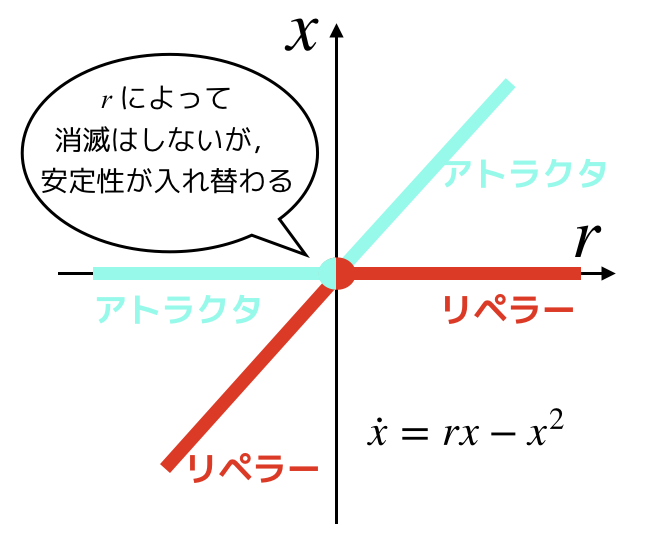
トランスクリティカル分岐の場合は，パラメータrの値によって，安定性の交換が起こります．
これはロジスティック方程式（xとrがどちらも正負を取ることに注意）や単一種類の増加を表すモデルに見られます．
ピッチフォーク分岐
３番目の分岐です．
発生も消滅も変化もやったし，もうないでしょ！？
と思っている方もいるかもしれませんが，数学は不思議な世界です．
もっと面白い分岐があります！
それがこれ，ピッチフォーク分岐です．
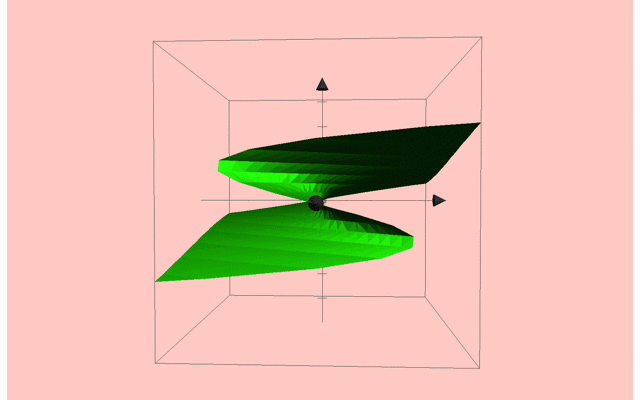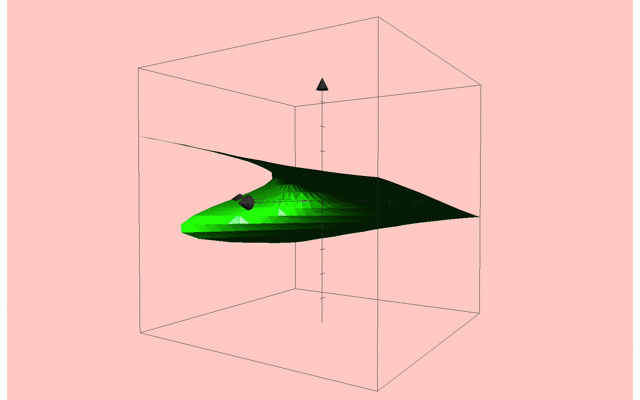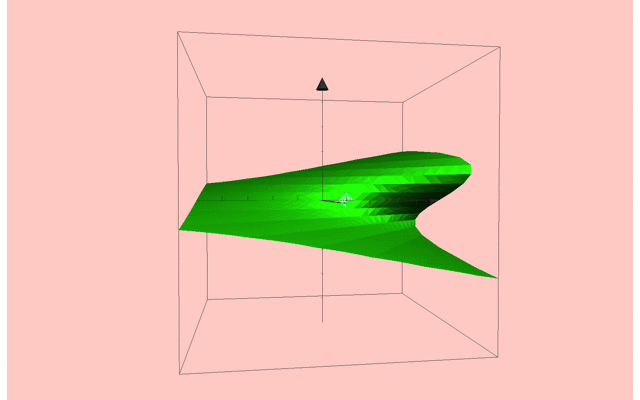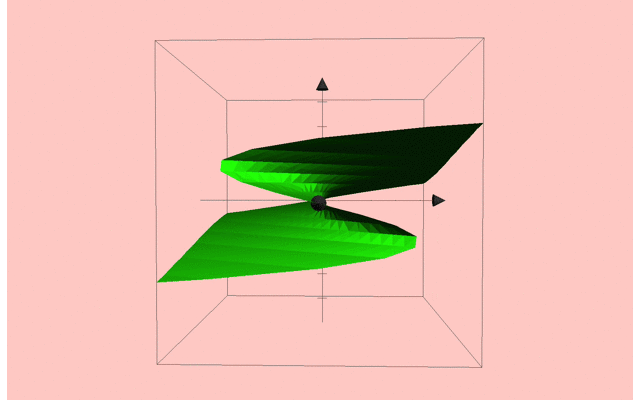
点対称性がある系です．
この系では点対称性があるため，xも-xも同様な取り扱いです．
固定点は対称的に発生・消滅が起こります．
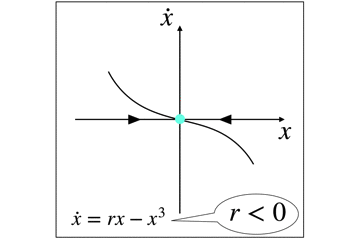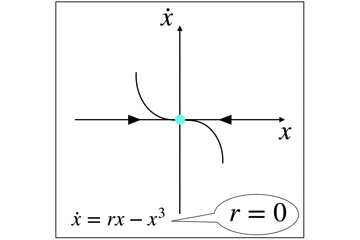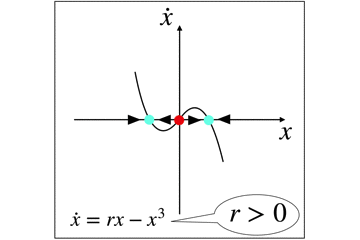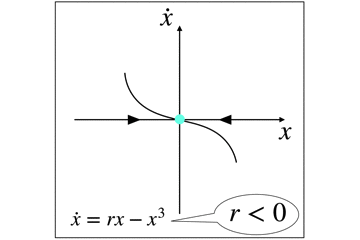
r<0の時には，原点のみが唯一の安定固定点（アトラクタ）です．
r=0になると，項の線形部分が消え，非線形のxの3乗の項しか残りませんが，ギリギリ安定固定点です．
このr=0の状態だと，解の減衰はものすごく遅くて，臨界減衰と呼ばれたりします．
r>0の状態になると，これまで安定固定点だった原点は，不安定になります．
しかし，2つの安定固定点が原点の対称的に発生します．
ちなみに，上で示した系は超臨界ピッチフォーク分岐といいます．
ちなみに，「ピッチフォーク」という名前の由来は，rの増加によって固定点が3つ出現する所から，「ピッチフォーク」の意味である「熊手」あるいは「三つ叉」という来ています．
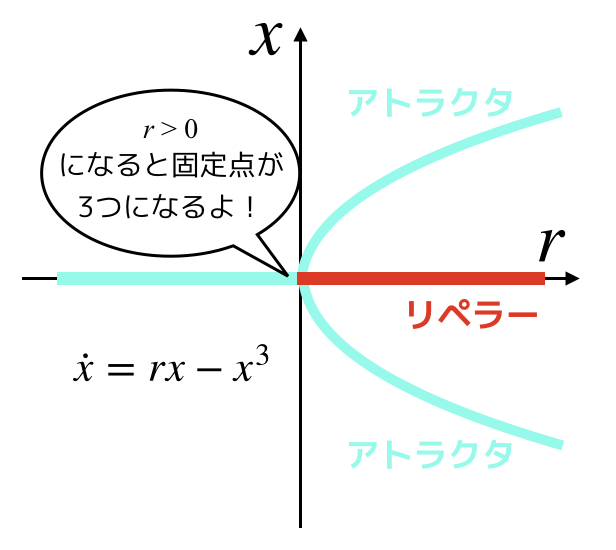
超臨界ピッチフォーク分岐は，３次の項が原点の固定点を安定化していて，いかなるx (or -x) をx=0 へ引き戻す復元力へと作用していました．
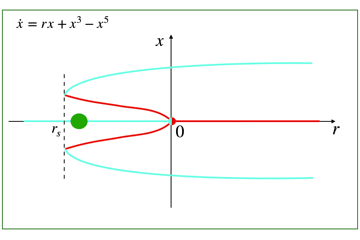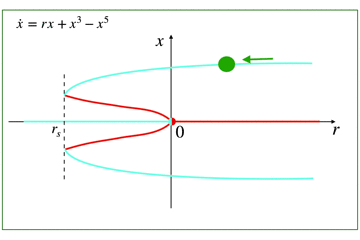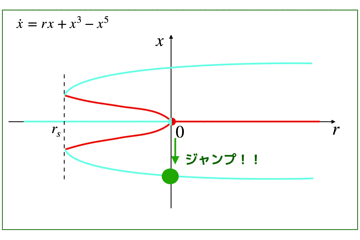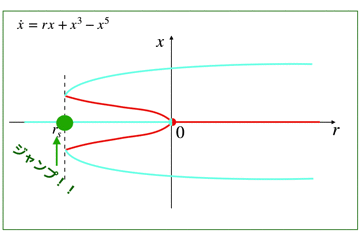
しかし，それとは逆に３次の項の符号がプラスである場合は，亜臨界ピッチフォーク分岐といいます（３次の項が不安定化させる働き）
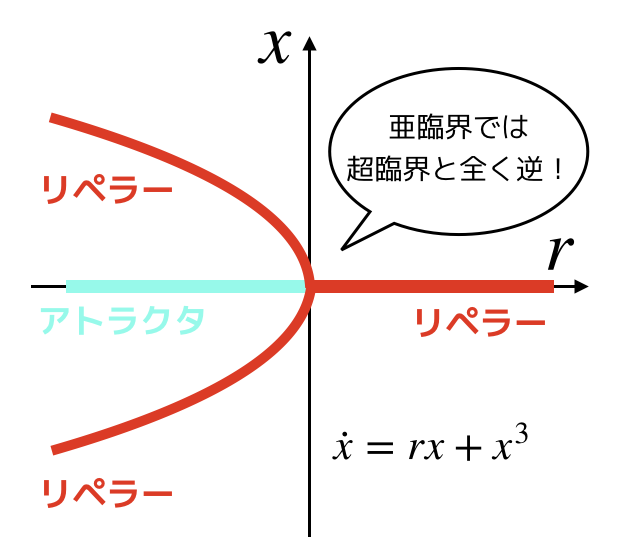
原点に関しては，超臨界と同様に，r<0で安定，r>0で不安定であるが，r>0の不安定な状態では，３次の項に妨げられてはいないことが大きなポイントです．
（むしろ3次の項は，解を無限大へと向かわせる手助け！！→ 解の爆発！！）
つまりこの状態では，初期状態のx0から，t→∞でxは発散することを示すことができます．
そのため，安定化の際には，3次のプラスの項の次に，5次のマイナスの項を導入することになります．
この亜臨界ピッチフォーク分岐に関しては，こちらの方に詳しくかいているのでどうぞ！
（記事：亜臨界ピッチフォーク分岐からジャンプやヒステリシス性を見る）
以上簡単な分岐についてでした．
ダイナミクスの定性的な変化を見るために，分岐が生じるパラメータ値というものは重要な要素になってくると思います．
分岐の概念は，工学系でも割と重要で，何かしらの制御パラメータを求める際に，安定不安定などを決定づける，いわばモデルを動かす際の指標になり得ます．
詳しくは本ブログで参考にしたこちらの参考書をどうぞ．
解説動画について
Youtubeで解説動画も出しました．
