- 分岐や数学,工学な話題が好きな人
- 2次元の流れに興味がある人
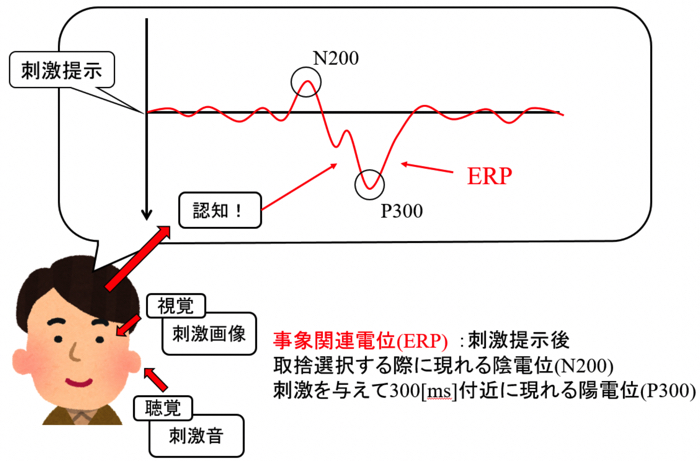
- 脳波とか日常の非線形やカオスに興味津々な人
こんにちは.これまで1次元のベクトル場の記事を読んでくださいました方々,どうもお疲れ様でした!
今回からは,ついに2次元に凸です!!!
ちなみに,まだ1次元の話を読んだことがないよー(><)っていう方は,以下で見る事ができるのでどうぞ!
(1次元の微分方程式の会をベクトル場を用いて図的アプローチで求めてます)
さてさて,相変わらず「ストロガッツ 非線形ダイナミクスとカオス」にはお世話になっております.
ありがとうです.
というわけで今回もやっていきましょう!
2次元の線形系です!!!!
2次元の線形系の定義について
二次元の定義については以下のようにします!

これからは相平面という言葉も乱用すると思うので,x-y平面の2次元の変数を扱う系なんだな!と思ってください!
ただし,xとyそれぞれの微分の結果は,1次の項から成り立つ単なる線形型のために,これを2次元の線形系という風にします.
単純な調和振動子!!
今回は導入として,単純な調和振動を扱います!以下のような系です!
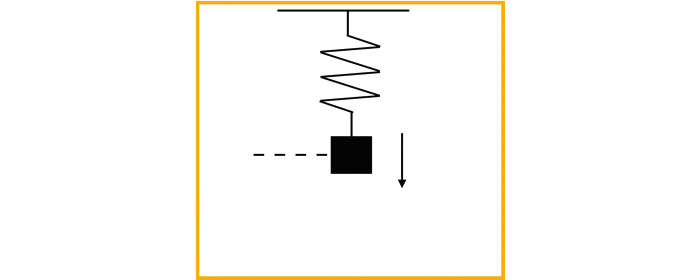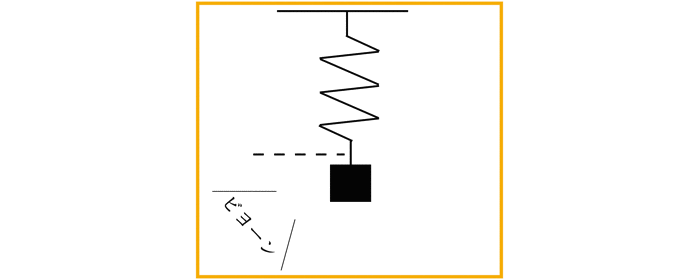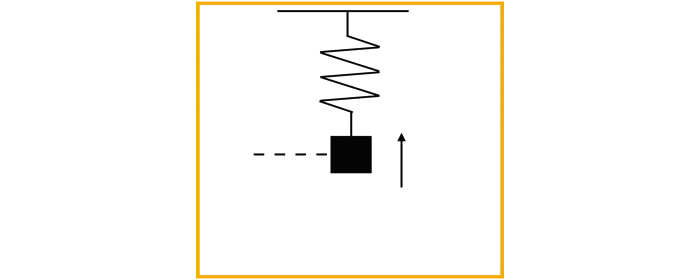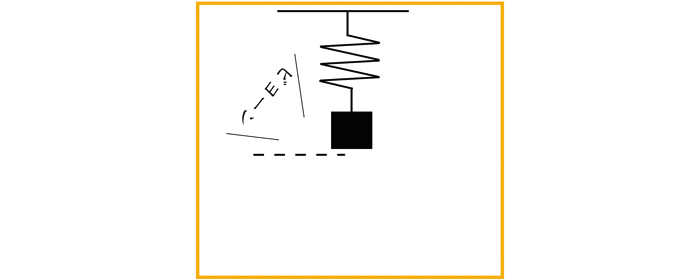

sinとかcosとかの三角関数を使った解析的な解法ではなく,相平面の解析を行います.
(線形方程式はsinとかの解析的な解法で解くことができるが,後々扱う非線形な問題ではいずれ対処することができなくなるため!)
相平面の解の挙動は,微分方程式に対応するベクトル場によって定まります.
ベクトル場の導出は,系の位置xと速度vが分かれば良いです.
そこで,位置xと速度vの情報を得るために,調和振動子を以下に書き直します.

ベクトル場
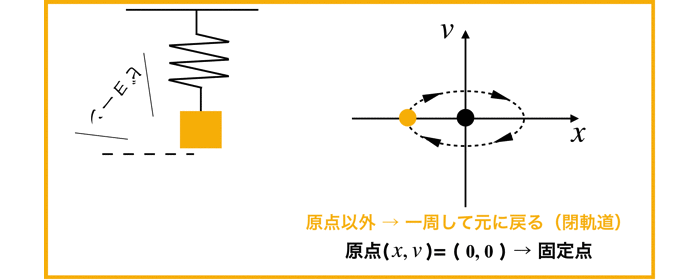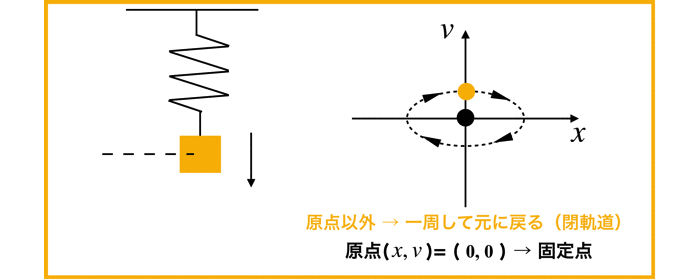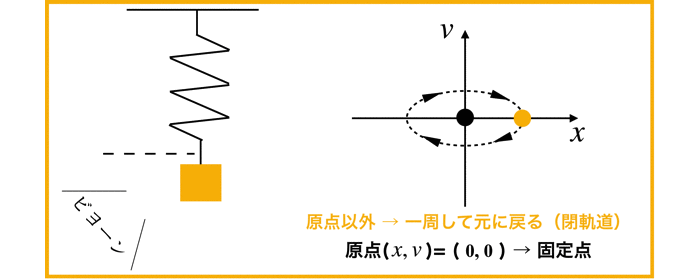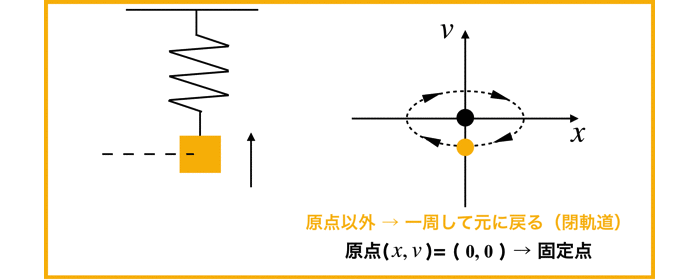
各位相平面(x,v)についてベクトルを計算すると以下のようになる.

初期条件が原点の位置では,xおよびyがそれぞれ0なので,微分値も0です.
すなわち,この状態では相空間上にいつまでも静止したままの状態です.
しかし,初期条件x=1 (例えば質点mを引っ張り手を離す)などを加えると,相空間の中をぐるぐると回る軌道を見ることができます.
すなわち,閉起動となり,質点の周期運動(振動)が対応します.
閉軌道の形状
ちなみに,以上の閉軌道ですが,面白い物理的解釈ができます.
この閉軌道が示す図形は,以下の方程式(楕円)と同じ形状をとります.
![]()
これが,上のベクトル場で書いた楕円とエネルギ保存則的に等価であれば良いのですね.
ということで続きはまた次のブログで〜!