- 数学とか物理とか工学が好きな人
- 固有値とか固有ベクトルについて学びたい人
- 2次元線形系の方程式に興味がある人
こんにちは.けんゆーです(@kenyu0501_)
前回は2次元線形系の相図をやりました.
(2次元線形系ダイナミクスの安定性の図的理解と専門用語について!)
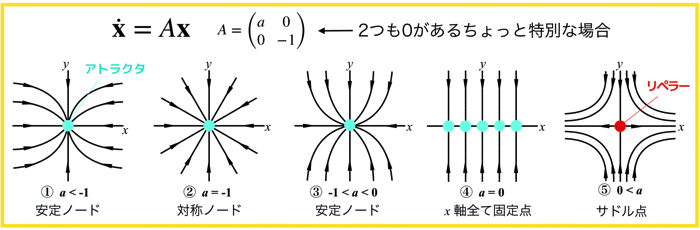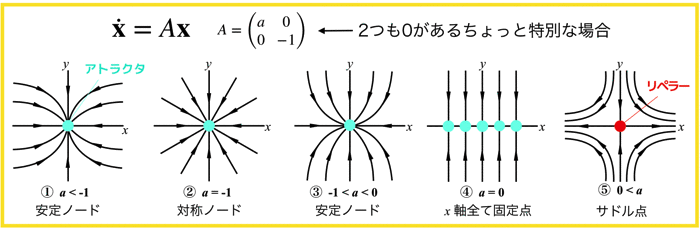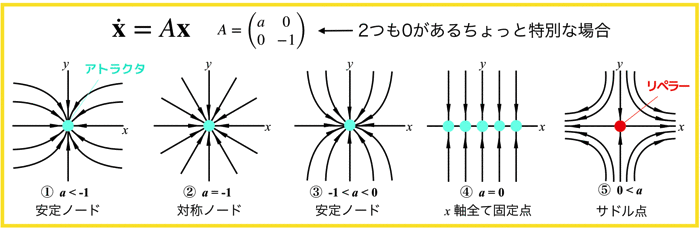
上の例は行列式Aの中の成分が2つも0があり,xとyの解がお互い独立で影響を及ぼさない場合でしたね.
そこで今回はもっと一般化して,行列Aの成分がびっしりと詰まっている状態の方程式を解いて相図を確認していきたいと思います.
そのためには,固有値や固有ベクトルなんていう概念も必要になるので,その辺をおさらいしつつ話を進めていきます.
また,2次元非線形の相平面に関してはこちら!!
(参考:2次元非線形の相平面をPythonで書く)
扱う問題について
またまた今回も「ストロガッツ 非線形ダイナミクスとカオス」から引用して問題を解いていきます.
以下で問題をガリガリとりあえず解いていきましょう!

結構長かったですが,行列Aおよび与えられた初期条件に対する解を求めることができました!
特性方程式や固有値,固有ベクトルを計算して解を求めていきました...が!!!
線形系の相図を記述するにあたっては,固有値と固有ベクトルさえ分かっていれば実は良いのです.
いちいち,最後の解を導出しなくても良いのですね〜!
相図は?
さてさて,相図を書いていきましょう!ここで

2つの固有値がそれぞれプラスとマイナスを取るので,一つの固有解は指数関数的に増加,もう一つは減少ということがわかります!
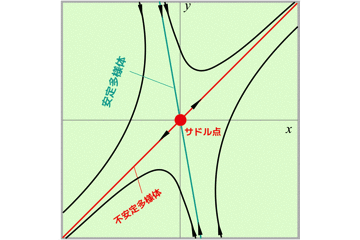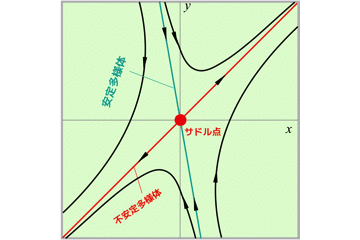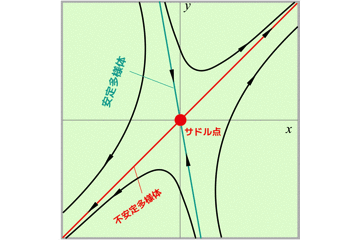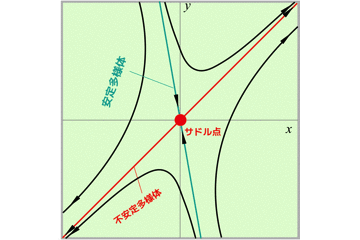
すなわち,原点はサドル点であることが分かります.
(おさらい:「2次元線形系ダイナミクスの安定性の図的理解と専門用語について!」)
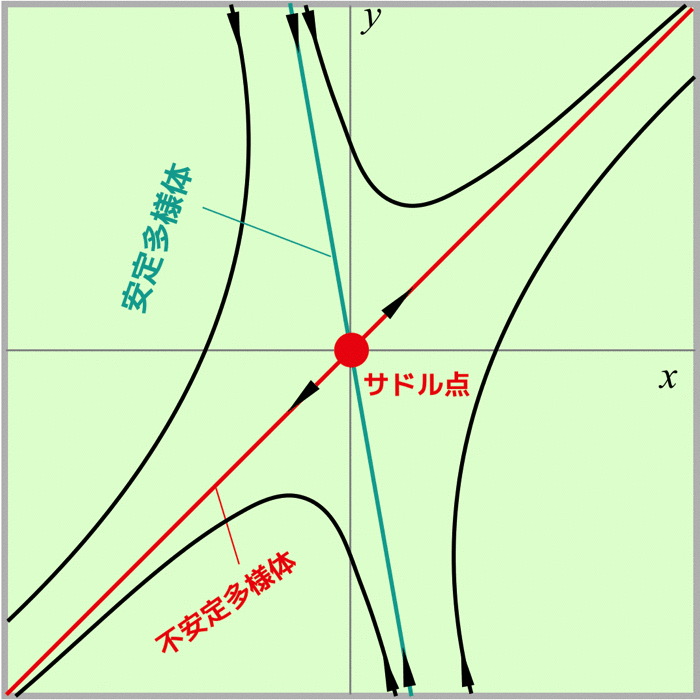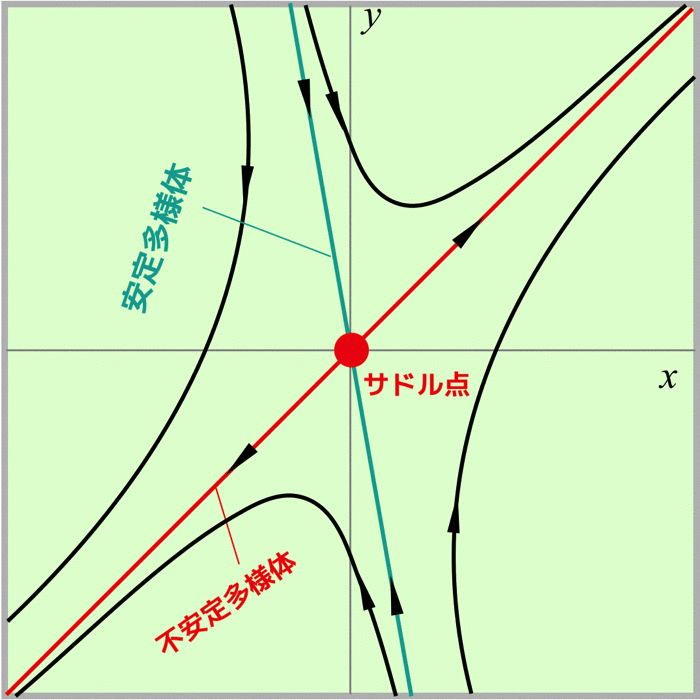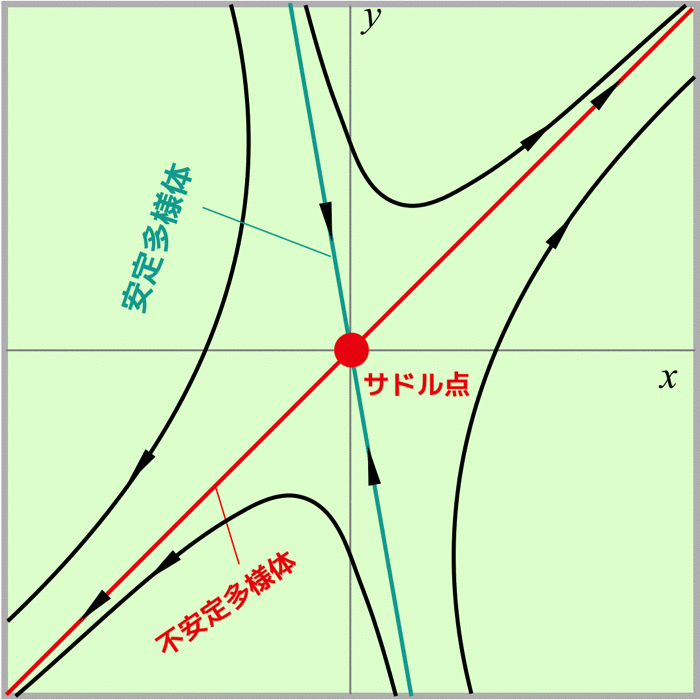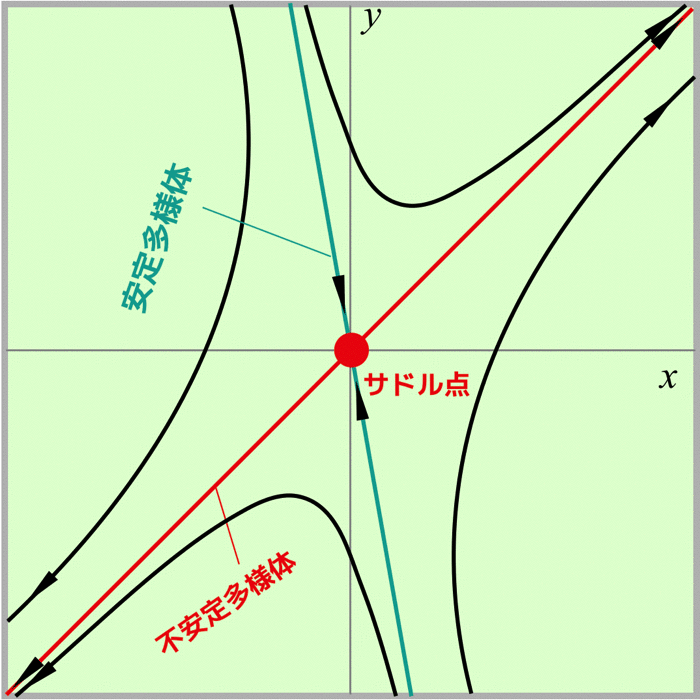
さらに,安定多様体と不安定多様体は,固有ベクトルに対応します.
ここで,安定多様体の方は固有ベクトルv_2=(1,-4)が与える直線となります.
(これは減衰する方の固有値λ_2の方)
逆に不安定多様体はv_1=(1,1)です.
サドル点での軌道を確認すると,t→∞で不安定多様体に近づき,t→-∞で安定多様体に近づきます.
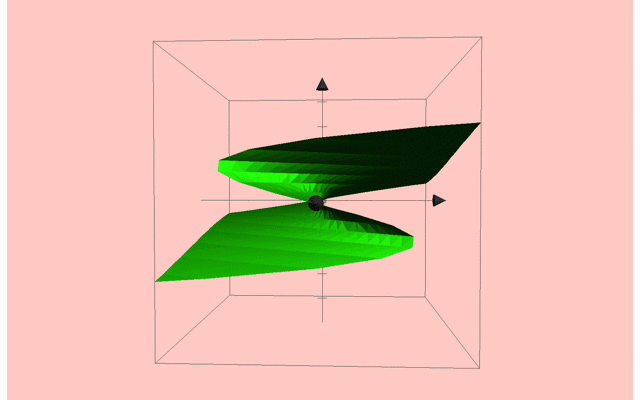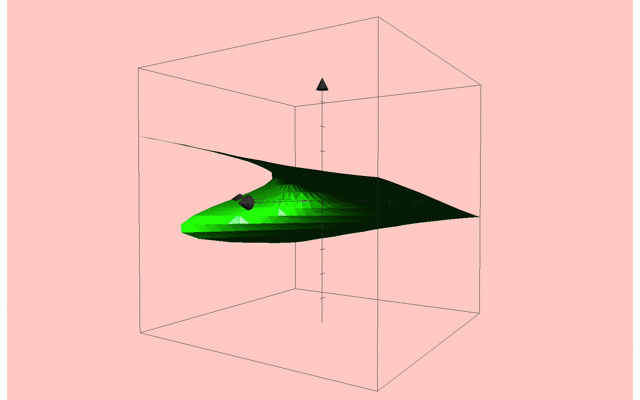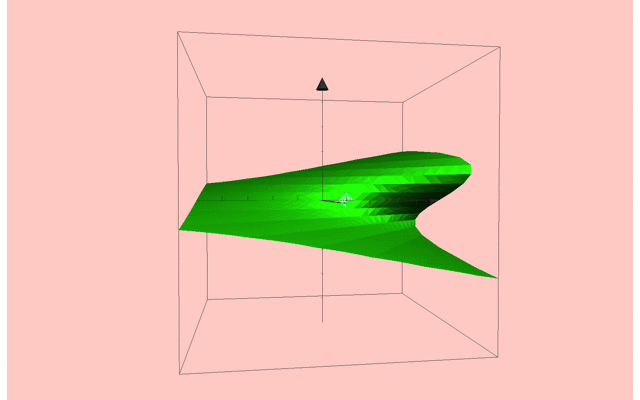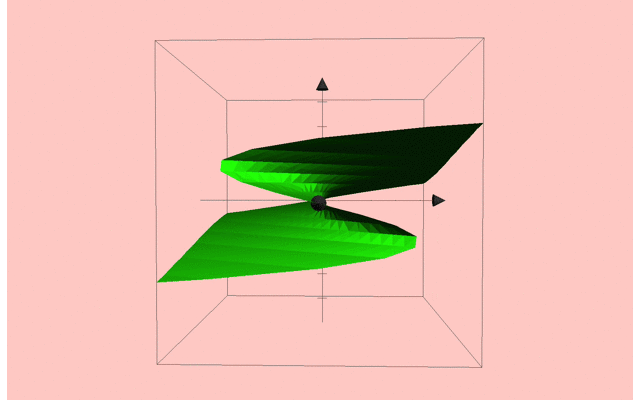
ここで,相図は以下のようになります.
その他いろんな相図もあるよ!
二つの固有値がとりあえず負であればどちらも固有解も指数関数的に減衰し,安定ノードになります.
これは予想できると思いますが,減衰の速度が違ってきます.
また,固有値が複素数の場合は,センターやスパイラルと言われる形状のどれかになります.
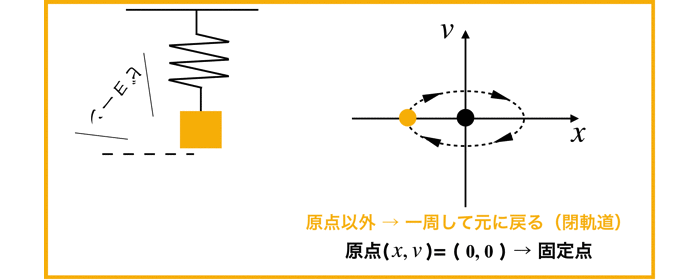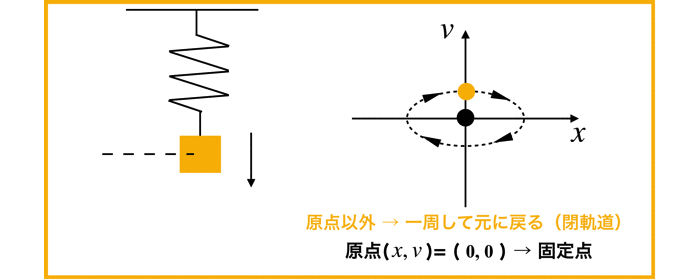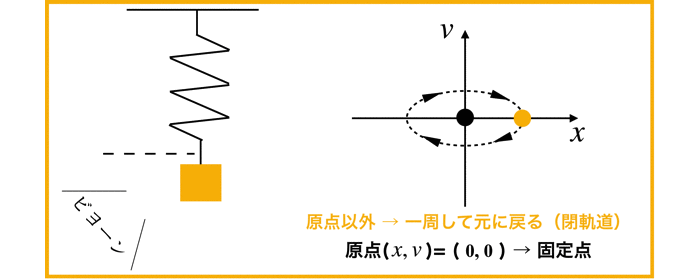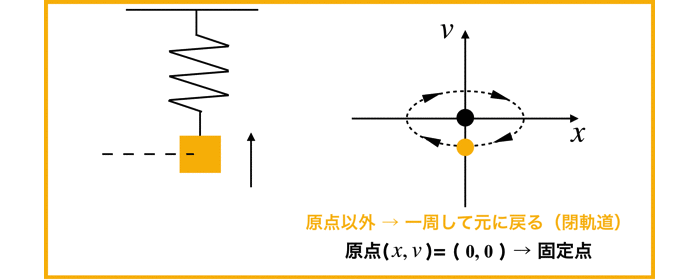
以前解いた調和振動子は,センターになりますね!
(参考:「(2次元の線形系)単純な調和振動子の相図をかく!」)
ちなみにセンターの状態は中立安定です.
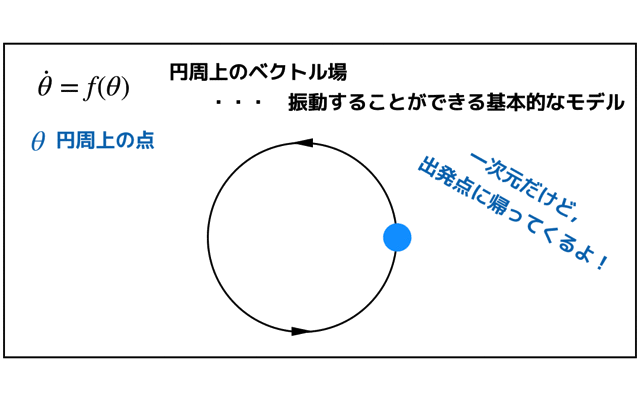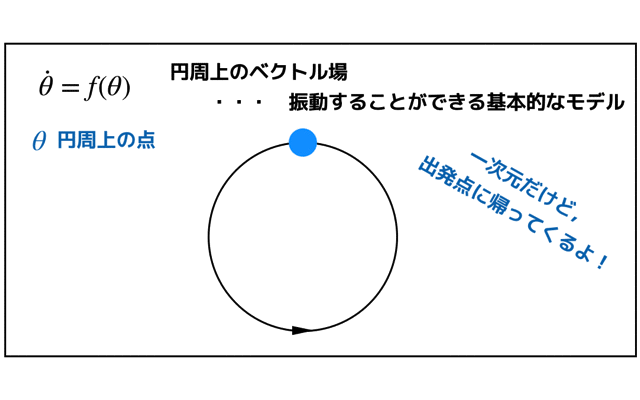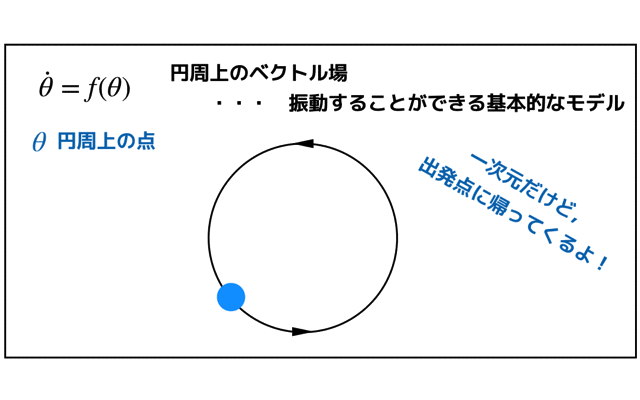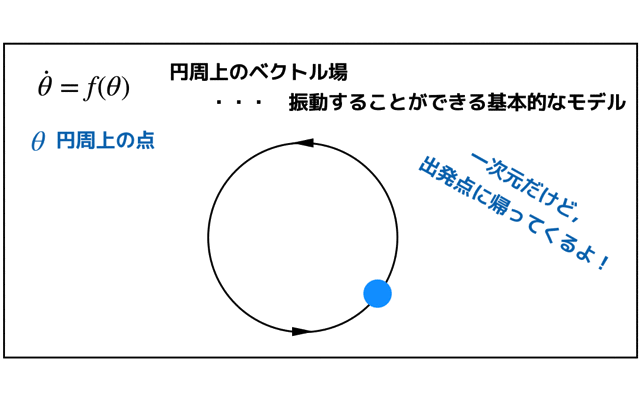
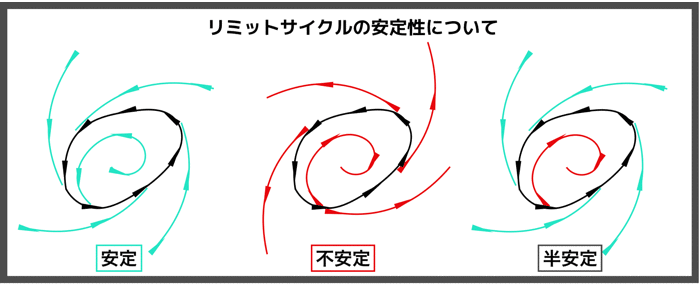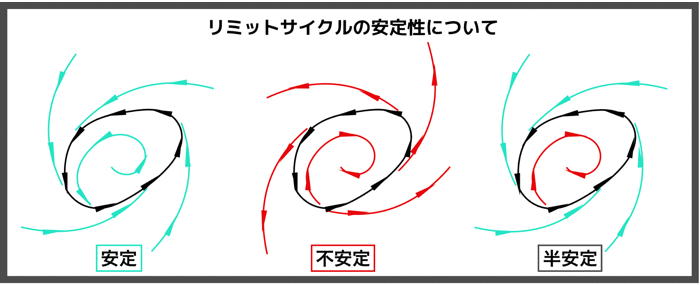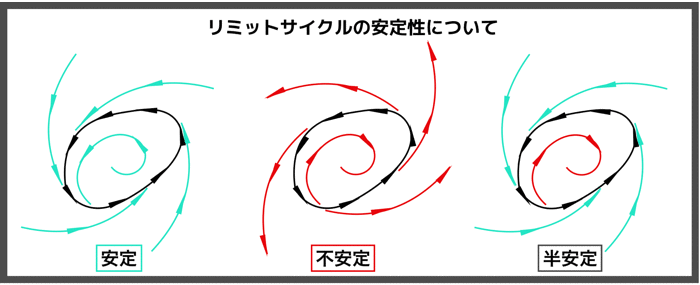
また調和振動子が少しでも減衰されると,スパイラルが現れます.
(振動子の1回転ごとにエネルギ損失がある)
また今度詳しくやっていくかもです!
色々と面白い側面があるので他にも取り上げていきますね!!




ストロガッツ先生の非線形ダイナミクスとカオスを勉強しているものです。
よく判らないのですが、
固有解 x(t)=e^2t+e^-3t Y(t)=e^2t+-4*e^-4t
に対する相図x,yですが, グラフでは x は、正負どちらにも描かれていますが、式を見れば判りますように、tをどう操作しても x は正にしかならないわけでして、負側が、なぜ描かれているのか判らないのです。
ストロガッツ先生も、間違っているのでしょうか?
至急お返事をお願いします。