- 機械工学を学んでいる人
- 動力学(ダイナミクス)に興味がある人
- 非線形系解析を行うための準備をしている人
こんにちは.
今日は,ダイナミクスの安定性を議論するときに重要になってくる用語について確認していきます!
動力学の参考書とかを読んでいると,リアプノフ安定とか中立安定とか,たくさんの専門用語が出てきます.
後々混乱しないようにここでちょっと例題を軽く解きながら確認していきましょう!!
また,非線形系の固定点を解析する時に非常に役に立ちますよー!
また,2次元非線形の相平面に関してはこちら!!
(参考:2次元非線形の相平面をPythonで書く)
扱う問題について
相変らず「ストロガッツ 非線形ダイナミクスとカオス」を参考にしてます.
以下の線形系を解いていきます
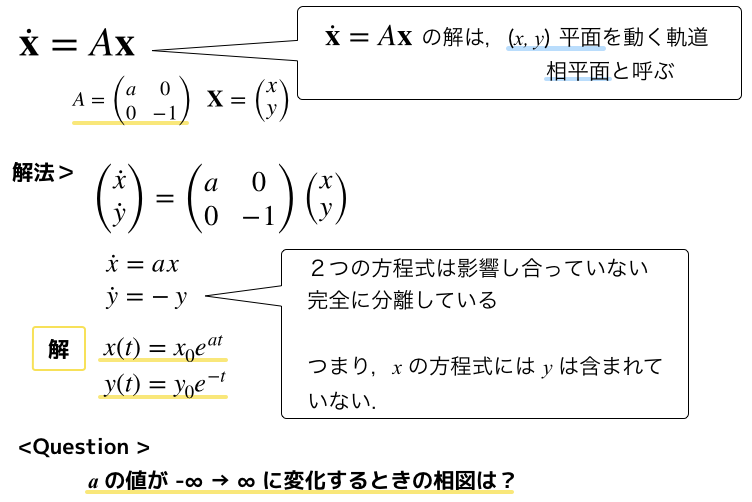
解を確認すると,xとyがそれぞれ分離していることがわかります.
お互いに,時間tに対しての挙動を表しますが,それぞれx,yの挙動は独立的に取り扱っても大丈夫そうです.
ここで,yの解を見てみると,yはパラメータaの値の影響を受けずに,時間的に指数関数的減少が生じることが予想されます.
e の (-t) 乗ですもんね!時間tに対して指数関数的減少ですね.
しかし,xの解に関しては,パラメータaの影響がありますね!このaの値によって安定性が変わってきそうです.
もちろん,aの値による安定性の変化は,相図の変化として見ることができます.
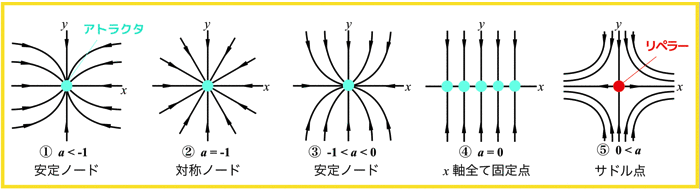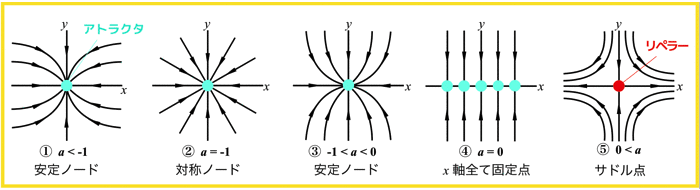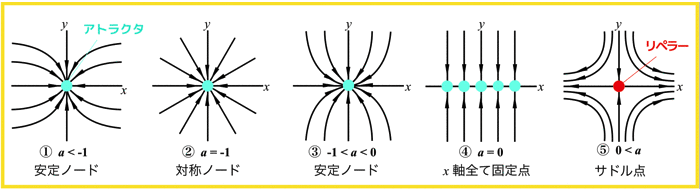
今回は以下の5種類に大別できそうです!
- a < -1 (安定ノード)
- a = -1 (対称ノード)
- -1 < a < 0 (安定ノード)
- a = 0 (直線が固定点)
- 0 < a (サドル点)

① a < -1 (安定ノード)
この場合は,xもyも指数関数的に減少をしますが,a<-1 (yの方はe^(-t))なので,xの減衰の速度の方が猛烈に速いです!
そのため,相図のベクトル場の形状としては,以下のようになります.

各象限のベクトル場の方向は,xの減少スピードの方がはるかに速いので,y軸の方向に向かいます.
y軸に近づいてくる(ほぼ接しているかもしれない)と徐々に向きを変え,アトラクタである原点に向かいます.
またこの時の固定点(x=0)を,安定ノード (安定結節点)といいます!
② a = -1 (対称ノード)
xとyの減衰率が同じ場合について考えていきます.

この場合は2つの方向の減衰率が同じなので,原点(アトラクタ)に向かって直線的になります.
こんな場合は非常に特別で珍しいです.
この場合のx=0は対称ノードやスターノードと呼ばれます.
③ -1 < a < 0 (安定ノード)
この時のベクトル場については,ほとんど①番と同じです!
xとyどちらも指数関数的に減少しますが,yの負の値が大きいために,x軸に叩きつけられるような形状を得ます.

こちらもx=0では,安定ノードですね!
④ a = 0 (直線が固定点)
ちょっと今までとは違いますね!
xの値が一定(x0)の場合です.

この時はx軸全てが固定点になり得ます.
すなわち全ての軌道は,x軸に垂直に向かいます.
⑤ 0 < a (サドル点)
ちょっとビジーですいません.
最後はリペラーになります.
x=0 に集まってこないものです.

しかしながら,初期値がy軸の上であれば原点に来ます.
この場合,x=0 はサドル点といって,唯一安定だったy軸を,サドル点の安定多様体といいます.
(安定多様体を厳密に定義すると,「t→∞で,x→サドル点 となる初期条件x0の集合」ということになります.)
逆に,「t→-∞で,x→サドル点 となる初期条件x0の集合」の場合は,不安定多様体といい,現在の例ではx軸がそれに当たります.
時間をマイナスの無限大に飛ばした時に,xがサドル点に集まるところですね!
その他専門用語など

上の絵にその他専門用語を集約させました.
ざっくりと解説しておくと,極限的に固定点に向かうものを吸引的と言ったりします.
①〜③のケースです.
また,極限的ではないですが,全ての時刻でのふるまいが固定点付近にあるものをリアプノフ安定と呼びます.
吸引的でありリアプノフ安定であるものを安定とか漸近安定とかって呼びます.
さらに,リアプノフ安定であるが,吸引的なものではないものを中立安定と言います.
④みたいなケースですね.
⑤は不安定です.
リアプノフ安定にも吸引的でもないためです.
中立安定のほかに,吸引的であるが,リアプノフ安定ではないものもあります.
これは,吸収的に全ての軌道を原点付近に吸収しますが,そこの付近までくると,大きな運動をするものです.
(例えば dθ/dt = 1-cosθ があります)
大体は以上です!
ぜひ何度も読んで覚えてくださいねー!