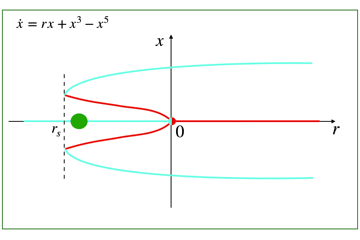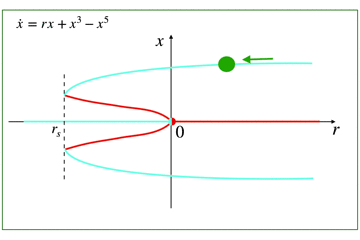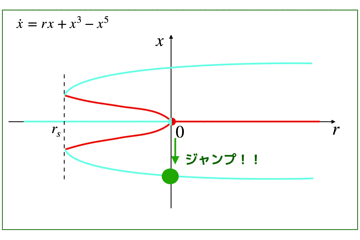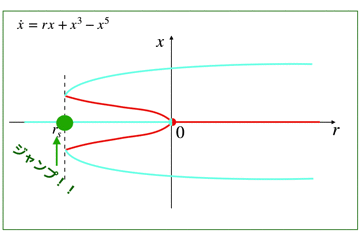
- 物理とか数学とか工学が好きな人
- 非線形ダイナミクスとか相図とかも好きな人
- 2重井戸ポテンシャルに興味がある人
こんにちは.けんゆーです(@kenyu0501_)
2重井戸ポテンシャルってご存知でしょうか.
量子力学とかやっていたり,バックグラウンドが電気電子工学なんかだと常識的なことだと思いますが,もし詳しく知りたい方はwikipedia先生を覗いてみてください.
(参考:井戸型ポテンシャル)
誤解を恐れず簡単に言ってしまうと,井戸の中にボール(粒子とか量子)があって,その周りに高い井戸型の壁があります.
(高い壁というのは一種の比喩で,環境よって作用される引力とかなんとか)
そして,それを飛び越えるためにはもちろん何らかしらのエネルギいりますよね.
井戸というか,落とし穴に落ちて出てこれない状態で,それを抜け出すには,壁を登るためのエネルギいるよね??
あーなるほど,位置エネルギ的なやつか!!!
みたいなノリでいいと思います.
この記事は分かりやすいです.
(量子力学〜井戸型ポテンシャル中の粒子〜)
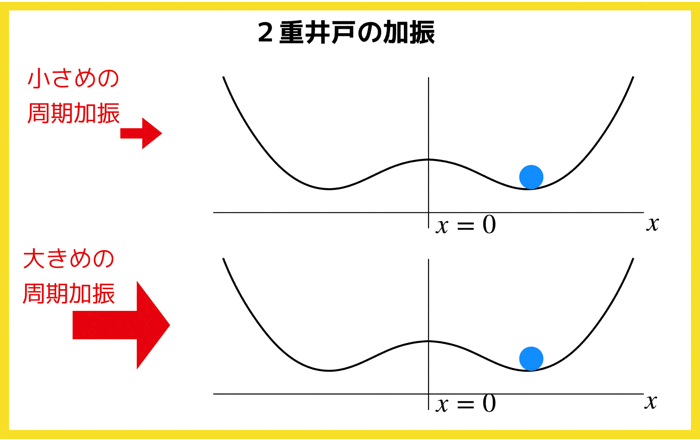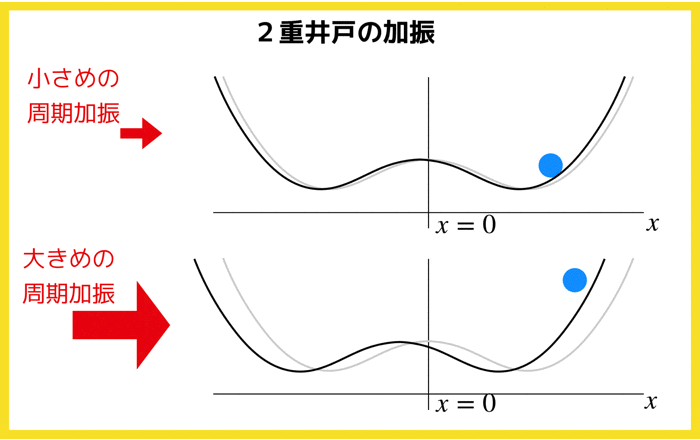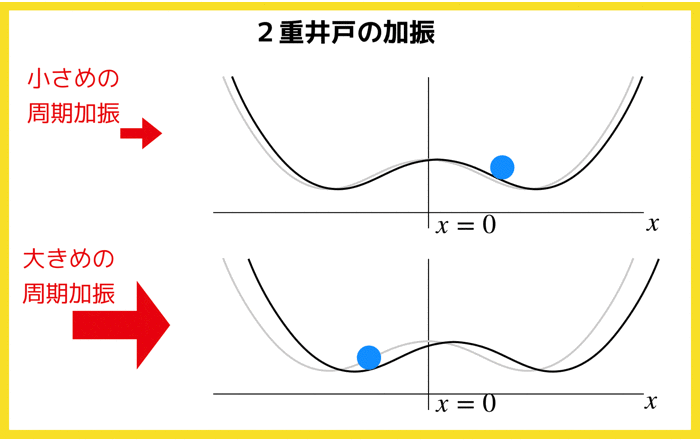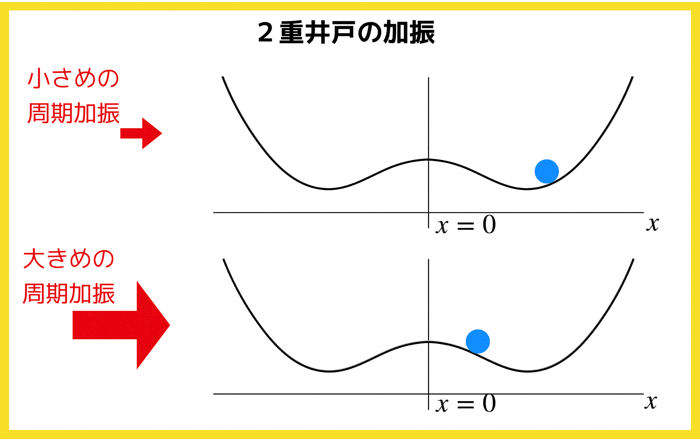
さてさて,この記事では以下の2重井戸ポテンシャル
![]() の中を動く粒子mを考えてみます.
の中を動く粒子mを考えてみます.
2重井戸ポテンシャルの相図
参考図書は「ストロガッツ 非線形ダイナミクスとカオス」ですが,きちんと計算して自分で全て試してますので,ご了承を...笑
では,系の相図と全ての固定点を導出していきます.
系の相図についてはこちらです.


また,同時に3Dアニメーションも同時に記載しておきます.
(2重井戸ポテンシャルのエネルギEを導出してほしいと言われたらやります...笑)
(ご要望はTwitterまで,,,)
2重井戸ポテンシャルの相図の特徴
以上の相図から,以下のような特徴が見られます.
- E=(1/2)y^2- (1/2)x^2+(1/4)x^4の等高線になる.
- 以上のEによって表される閉曲線になる.
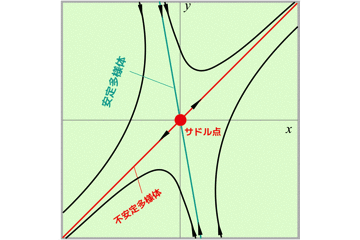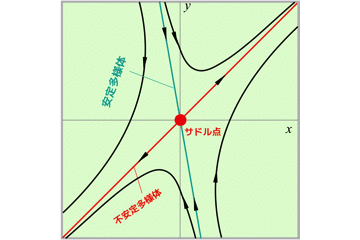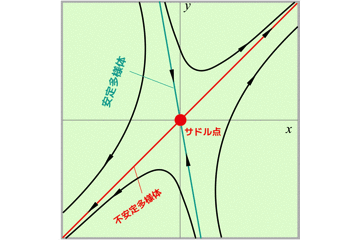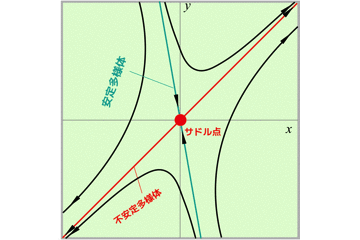
- (0,0)はサドル点
- (-1,0)および(1,0)はセンター(中立安定)
- センターは小さな閉軌道に包まれる
- 3つの固定点(サドル点とセンター)は大きな閉軌道に包まれる
- しかし,例外がある.
- 同一な固定点から出発して,そこの固定点に帰る軌道がある(ホモクリニック軌道)
- ホモクリニック軌道は,周期解ではない
- ホモクリニック軌道は,保存系でよく見られる
ここで,ん??保存系??となった人のために,以下に保存系についての簡単な解説をしておきます.
保存系とは
系の全エネルギーが,時間の関数として一定値をとるものを「保存系」として定義されます.

では〜!