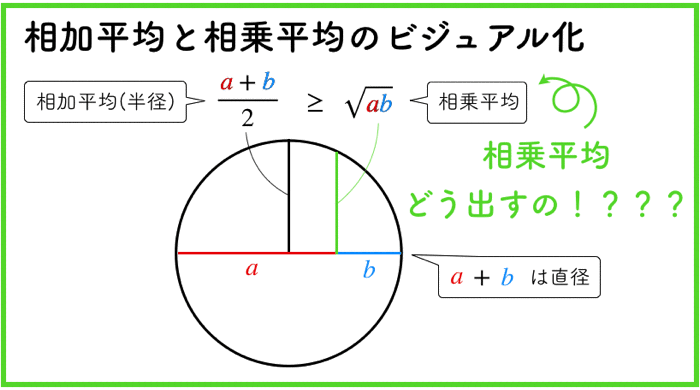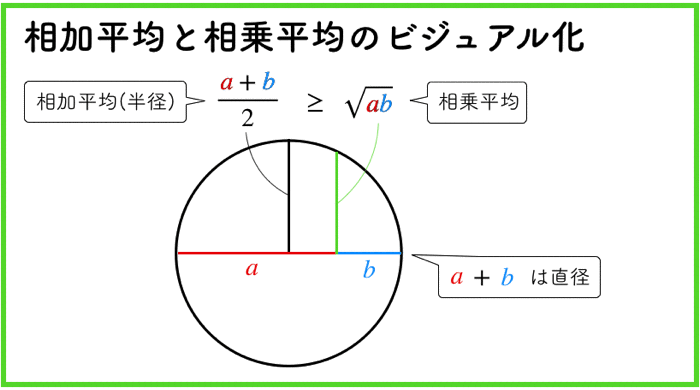
センター試験の対策として「黒本」の名前で知られる河合塾のマーク式総合問題集を使っている人は多いと思います.
このブログでは,黒本の問題,「第1回から第3回のすべての確率」の問題を一緒に解き進めたいと思います.
主に,どのように解いていくのが最適か?,解答を見てもいまいち理解できない所を取り上げていきます.

一緒に頑張っていきましょ〜!
問題集をお手元に用意して下さい!
第一回 条件付き確率の本質!?
第一回は,よくありがちな袋からカードを引いて対決する問題です.
袋Xは1〜5のカード.袋Yは1〜10のカードが一枚ずつ入ってます.
条件付き確率以外は比較的簡単な問題だったと思います.
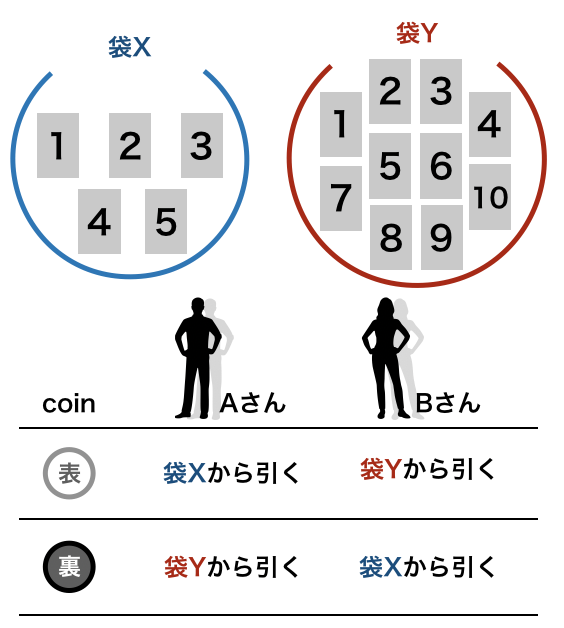
- コインを一枚投げる
- 表が出たら,AさんはXからカードを一枚引く.BさんはYからカードを一枚引く
- 裏が出たら,その逆でAさんはYからカードを一枚引く.BさんはXからカードを一枚引く
- 取り出したカードに書かれている数字が大きい人の勝ち!!
- 同じ数だと引き分け
- 取り出したカードは戻す
取り上げたい問題は(3)の条件付き確率です.
(それ以外は簡単なので)
問題(3):
ゲームを繰り返し行い,先に3勝した人を優勝とする.
4回目のゲームでAが優勝を決めたとき,4回目までに少なくとも1回引き分けが起こっている条件付き確率は?
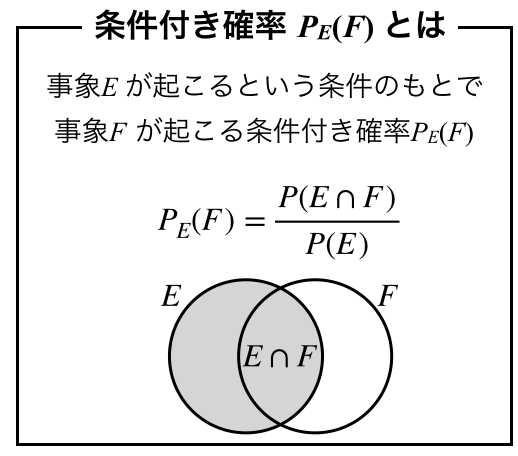
条件付きの条件とはどんなものか!?
条件付き確率って,上のような公式で教わったと思うのですが,こんな公式を丸暗記したところで意味はないのです.
きちんとこの公式や図の対応が理解できてはじめて,条件付き確率が分かった!ということになると思います!
ちょっと言葉を簡単に考えましょう!
条件って基本的にどういう事かというと,「考える範囲が全体から小さくなること」ですよね.
なので,条件付き確率はそもそも考えるべき範囲(分母,母数)が変わることなのです!
例えば,ある部屋に100人の男女がいるとします.
この中から無差別に一人選んで,車をプレゼントします!
っていう確率の問題だと100分の1ですよね!
100人に一人の確率で車貰えちゃいます!

こんなの当たるわけないよ〜
ここで,条件という概念をつけると,例えばこうです!
この中の女性の方から無差別に一人選んで,車をプレゼントします!
っていう問題だと,100人いる部屋のうち,女性だけに絞られるわけですよね!
考える範囲が狭くなりましたよね!
仮に50人しか女性がいなければ,確率は50分の1です.

ワンチャン当たるかも!
またさらに条件をつけて,
この中の女性で未成年の方から無差別に一人選んで,車をプレゼントします!
という条件がさらにつくと,もっと範囲が小さくなりますよね!
つまり考えるべき母数(確率でいうところの分母)が変わります!

おっ!見渡すと女性で未成年の人はざっと4,5人だから,これは車当たるぞー!!興奮してきたああああ
そのため,条件付き確率のだいたいの問題では,分母が全体より小さくなる(見る範囲が変わる)ので,確率としては増える場合が多いです!
それを踏まえて,問題を解いていきましょう!
問題を解く!
問題(3):
ゲームを繰り返し行い,先に3勝した人を優勝とする.
4回目のゲームでAが優勝を決めたとき,4回目までに少なくとも1回引き分けが起こっている条件付き確率は?
条件付き確率では,分母を考えることが大事です!
つまり,Aが先に勝つ場合のパターン(回数)って色々ありますよね.
例えば
- 3回目でAが勝つ
- 4回目でAが勝つ
- 5回目でAが勝つ
- 6回目で....
などなど,勝ち方という事象はめちゃくちゃ沢山のパターンがあるわけです.
しかし今回は,4回目のゲームでAが勝つ!と言われているので,分母は,「4回目でAが勝つときのみ」になります.
全体から小さくなりましたよね!
分母を決めることができれば,分子は楽勝です!
分子は,その条件の中で4回目までに引き分けが起きる事象を考えれば良いだけです.
つまりこうなります!
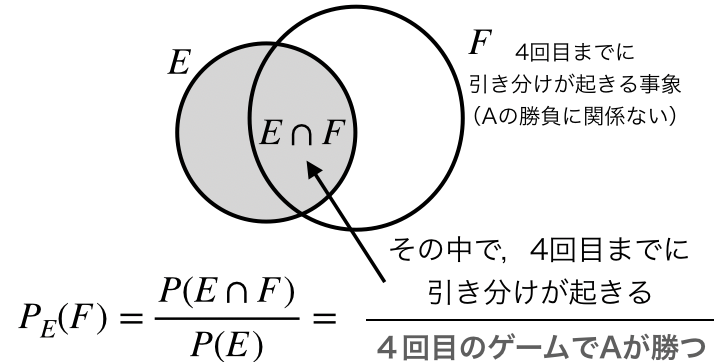
条件付き確率のこの公式と図の意味が理解できたと思います!
ちなみに答えは,2/11です!
各事象についての計算の答え合わせは,解答をみてください!
第2回 余事象の変形に気づくか!?
第二回は,袋の中にあるボールをサイコロの出た目に従って移すゲーム問題です.
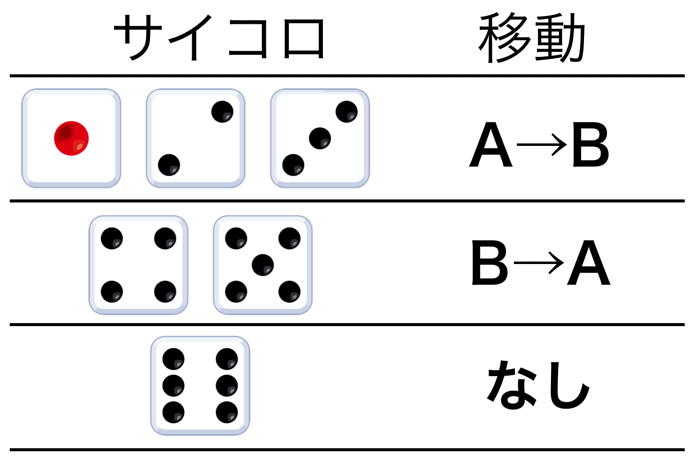
- 一つのサイコロを振る
- 1,2,3のいずれかの目が出たら,袋Aの中から一つの玉を取り出し,袋Bに入れる
- 4,5のいずれの目が出たら,袋Bの中から一つの玉を取り出し,袋Aに入れる
- 6の目が出たら,玉の移動を行わない
- 袋Aに入っている玉の個数をNとする
最後の問題(4)はちょっと難しいですね!
問題(4):
袋Aに赤玉が3個,袋Bに白玉が3個が入っている状態から始めて,操作を三回繰り返す.
操作を3回行ったあと,N=2となるか,または袋Aに入っている赤玉が2個以上になる確率は?
解き方
センター試験のほとんど最後の問題は,そのまま解いて計算すると難しい場合が多いです.
しかし,ちょっとした工夫で簡単に解けるというケースが多々あります.
(基本的に問題は人が作っているので,工夫して解けるように作られています.)
この問題は,操作を3回行ったあとの以下の
「N=2となるか,または袋Aに入っている赤玉が2個以上」
となる事象を直接的に計算するのは困難なので,全体の事象1から上の状態以外を引いて求めるということをします!

難しい問題はだいたい余事象を考えれば解決するのだ!
つまり,以下のような計算になります.
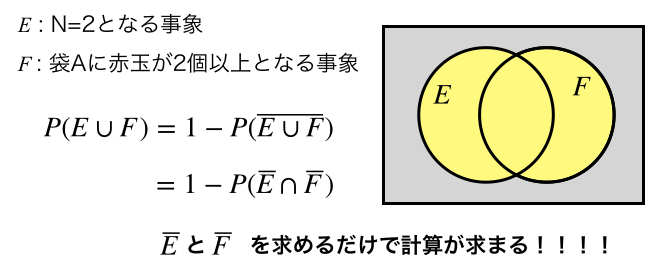
このような変形に気づくことができるかどうかが鍵です!
これができればあとは,
- E以外:N=2ではない
- F以外:袋Aに入っている赤玉が0個または1個
なので,
- E以外:3回ともA→Bへ玉が移動
- F以外:3回のうち,2回はA→Bへ玉が移動.残りは移動なし!
を求めたらあとは余事象を計算して終わりです.
答えは,3/4になります.

ちなみに,以下の変形はド・モルガンの法則というぞ!
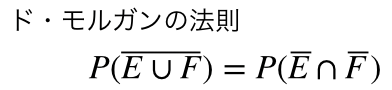
ド・モルガンの法則を面白おかしく理解したい人にオススメの動画は以下です.
(笑えます)
第3回
袋の中からボールを取り出しては戻し,みたいなよくありがちな問題です.
色違いや数違いのボールがあります.
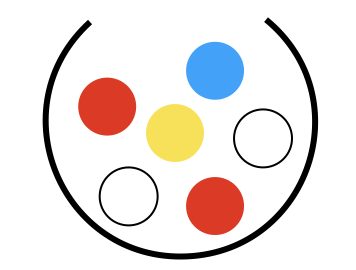
- 袋の中に,白球が2個,赤球が2個,青球が1個,黄球が1個の合計6個入っている.
- 袋の中から球を1個取り出して,また戻すという作業を繰り返す.
こういうシンプルな形式の種類は,かなりよく出るので,問題が難しくなりガチなんですよね.
案の定,この問題も結構難しい(というかめんどくさかったです)
条件付き確率が問題(2)と(4)で出てきます.
問題(2):
この試行を3回行うとき,3色の色を取り出すという条件のもとで,黄球が取り出される条件付き確率は?
問題(4):
この試行を5回行う.
1回目から4回目までの試行において取り出されない色の球があるという条件のもとで,さらに,もう1回試行を行うと4色の球が取り出される条件付き確率は?
条件付き確率を解く
条件付き確率の解き方は,まず分母を考えることでした!
それぞれやっていきましょう!
問題(2):
この試行を3回行うとき,3色の色を取り出すという条件のもとで,黄球が取り出される条件付き確率は?
求め方のファーストステップとして,分母である3色の色を取り出す確率を出すわけですが,これが非常にめんどくさい.
なぜなら,4色の球の中から,どの3色を取り出すかを別で考えないといけないからです.
ちなみに,3色の色を取り出すのパターンは以下の4つです.

ちなみに,以上の4つのパターンは,取り出す順番によってさらに通りが増えます.
例えば,( i )の白,赤,青の場合を考えてみると,
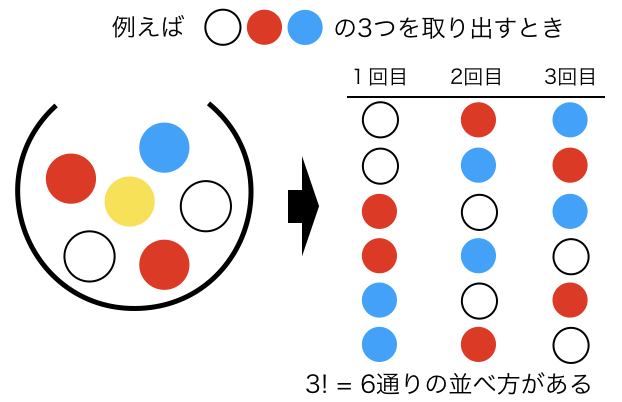
このように,1回目から3回目までで6通りの取り出し方が存在します.
これを考慮に踏まえて,分母にくる3色の球の取り出す確率を求めます.
ちなみに,求めると1/3になります.
次に,条件付き確率の分子です.
分子は,3色の球を取り出し,かつ黄球が取り出されるので,図のパターンの( ii )( iii )( iv )の場合になります.
すなわち,2/9です.
よって,条件付き確率は2/3ということになります.
(分子/分母=(2/9)/(3/1))
問題(4):
この試行を5回行う.
1回目から4回目までの試行において取り出されない色の球があるという条件のもとで,さらに,もう1回試行を行うと4色の球が取り出される条件付き確率は?
この問題も先に分母を考えるとやりやすいです.
分母はもちろん,「1回目から4回目までの試行において取り出されない色の数がある」という確率が入ります.
余事象をうまく使って計算をしてみてください!
分子は,「5回目の試行において始めて4色の球が取り出される」確率になります.
それぞれを丁寧に解くとできると思います!
めんどくさいですが,頑張ってみてください!
ちなみに条件付き確率の答えは,3/25になります.