
- 機械工学を専攻している大学生の人
- 物理や数学が好きな人
- 振動に関する分野が好きな人
こんにちは.けんゆー(@kenyu0501_)です.
機械工学出身なので振動系の基本的な記事を書きます.
モノ(構造物とか)においての振動は結構危険なものだったりしますので,作る段階においてよく考えなければならないものです.
それを学ぶために機械工学科では,物体の固有振動数を計測する実験をしたりします.
一般的に物体は,構造や密度等によって,振れやすい振動数(固有振動数)というものが存在します.
外から何らかの周期を持った力が加えられて振動する際に,その物体が持っている固有角振動数と外力の振動数が(奇跡的に)一致すると,共振といい,時には構造物が破壊されるようなエネルギーを発することがあります.

機械工学ではとても大事なものだぞ!!

代表的な例として,タコマ橋の崩壊(橋にぶつかる風の振動数と,橋の固有振動数が一致)とかがよく取り上げられますね!
アメリカ,ワシントン州のタコマナローズ橋は設計上の計算では風速60m/secまで耐えられるはずでしたが,たったの風速19m/secという風によって周期的なねじれ振動が生じ,ケーブルが破断され,完成から4か月で崩壊しました.
しかし風自体は周期的に吹いていたわけではなく,風が吹くことにより橋周りに渦が発生して,その渦からの周期的な振動と,タコマ橋自体のねじれ振動が共振を起こした結果です.
タコマ橋の崩壊の原因は主に剛性の小ささが代表的ですが,風と橋が作り出す渦による振動,橋自体の固有振動数などに対する設計が甘かったのも事実です.
モノを設計する上で,剛性や安全性,コストなども大事なパラメーターですが,固有振動数や動的作用を考えるのもとても重要なことです.
つまり,モノを破壊するときには,そんなに大きなエネルギは必要ではなくて,その壊したい構造物の振動特性を把握していたら,小さな周期的な加振で壊すことができます.

かっこいいな!魔法みたいな感じだな!
そこで,今回は物体を加振したときに,固有振動数などを確認し,共振現象についてちょっと考えていけたらと思ってちょっと長めなを書きます!
機械工学科の大学で行うであろう加振実験系のプロトコルをベースに今回の記事を書いていきます.
実験を通してやりたいこと
やりたいことは以下です.
- 梁と板(連続体かつ弾性固体)に対して周期加振および打撃加振実験をして,固有振動数と固有モードの測定を行う.
- 固有振動数がどんなものに依存しているか確認する.
- 固有モードによる波形パターンを観察し,共振現象についても考える.
この三つです.
ついでに,今回の実験を通して,FFTアナライザの原理をしっかり理解していきたいと思います!
とても長い記事になりそうなのですが,頑張って書きます笑

頑張るぞ!!
実験の原理(解析に際して)
今回実験の対象として取り扱う梁と板なのですが,数値解析も同時にしたいので以下の理論に基づいて数学的なモデリングをします.
集中質量系のモデル
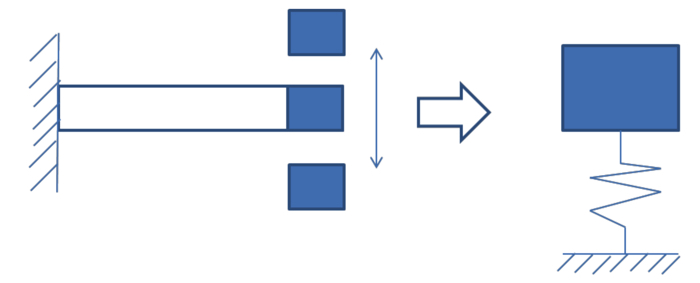
一つ目は,以下に示す集中質量系です.
下の図に示すように,質量が等しく,同じばね定数で支持された2自由度の振動系を取り上げることで,シンプルに固有振動数と固有モードについて考えることができます.
自由振動をする基本的なモデルですね.
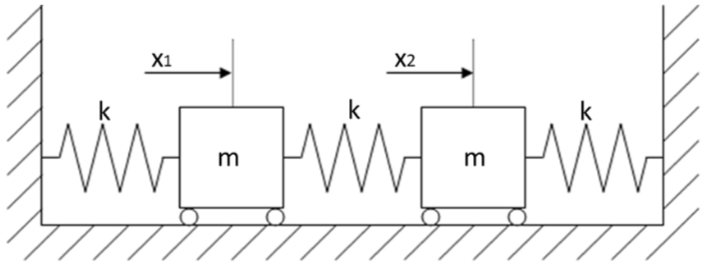
ここで,解析をするための数学的モデルを組み立てていきます.
(文字と数式が小さいので,スマホの人は適宜拡大して読んでください)

という解が得られます.
これら二つのxが2自由度系の自由振動の一般解であり,三角関数のtの前についている係数(√(k/m),√(3k/m),)は,値の低い順に第1次固有角振動数,第2次固有角振動数と呼ばれます.ちなみに単位は[rad/sec]です.
またAとBは振幅,φは位相を表してます.
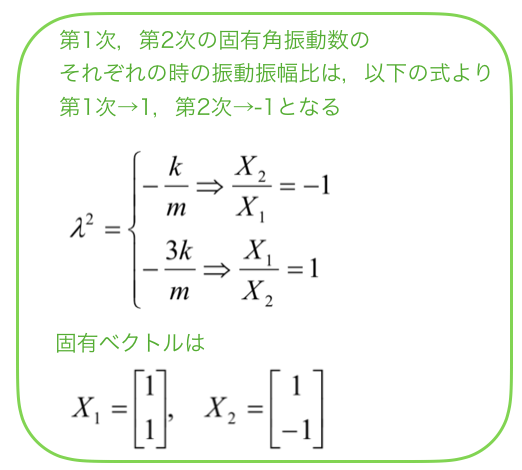
第1次,第2次の固有角振動数のそれぞれの振動振幅比は,第1次で1,第2次で-1になります.
固有ベクトルX1とX2は,上の図に示される系に固有の値です.
つまし,この系のモードは以下の図のようになります.
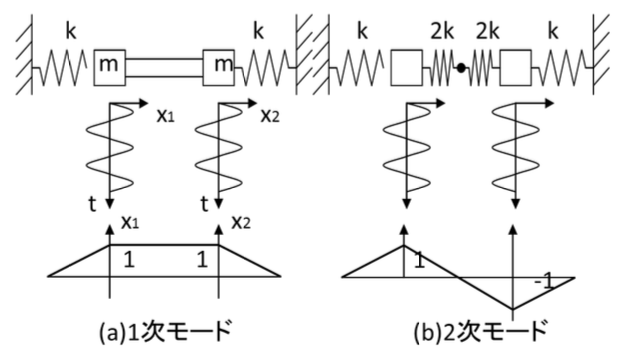
(a)1次モードの振動では,角振動数で2個の質量の振幅が等しく,同じ方向に運動します.
(b)2次モードの振動では,2個の質量は同じ振幅であるが逆方向に角振動数で運動します.
これは連結ばねkの中点が固定され,左右の質量に対してばね定数が2kとなったことに相当します.
このように2自由度モデルでは自由度の数に応じた固有モードが存在することになります.

これが集中質量系のモデルだ!
もう一つは分布質量系というものがあります.
運動を考える際,系を連続体としてモデル化すると,質量が分布した系となるので任意位置の運動を考えることができ,モデルに対応した固有振動数と各部の振動の様子を記述するモード形は無限に現れることになります.
分布質量系といいますが,これは以下で考えていきます.
分布質量系のモデル
ここでは,梁理論に基づき実験行う供試体の固有振動数と固有モードの計算を行います.
(前回は二つの質点を考えた自由振動モデルでしたね.)
ここで,実験を行う境界条件は片持ち(一端固定,他端固定)および両端自由としています.
まず,梁理論に関する説明をしていきます.
以下の図に示すような密度,断面積,縦断面係数,断面2次モーメント,長さの梁を考えます.
(軸線方向の変位をxとしてます)
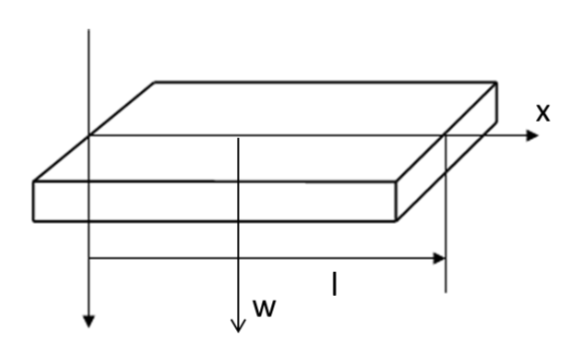
(文字と数式が小さいので,スマホの人は適宜拡大して読んでください)
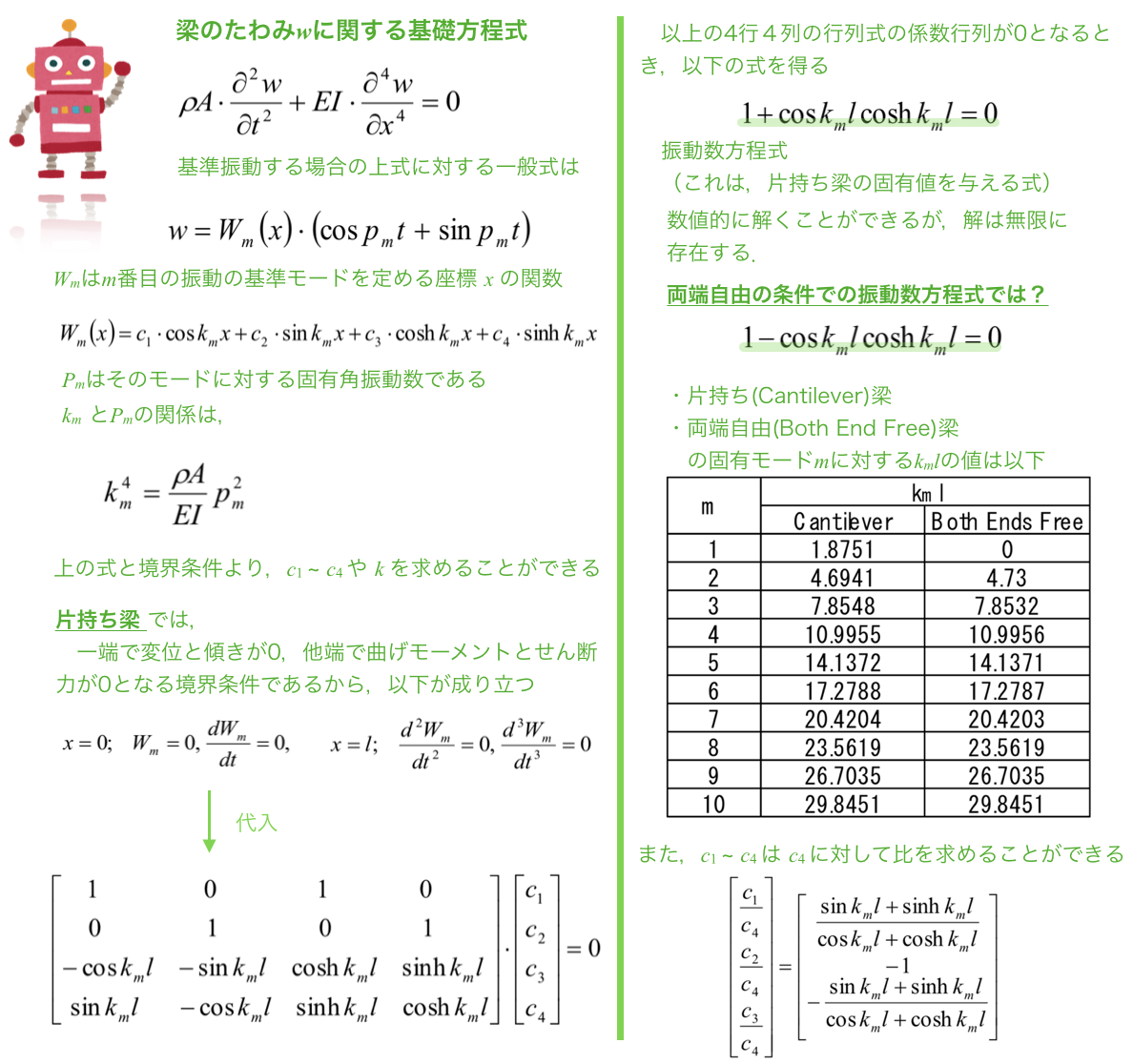

このように梁モデルでは,Kmlが無限個求まるので,固有角振動数は無限個存在することになります.
よって,対応する固有モードも無限個あります.
さらに,振動モードも分布形状として連続関数によって与えられます.
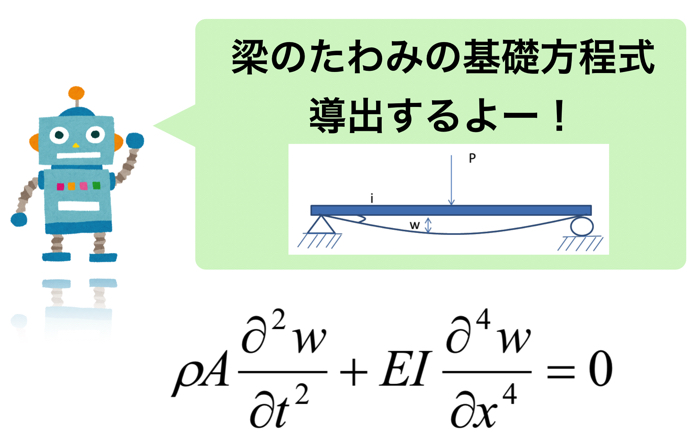
ここで,たわみの基礎方程式の導出が分からない方は,こちらを参考にしてみてください.
この記事はこんな人にオススメです. 機械工学を専攻する学生 梁のたわみなどに興味がある人 振動工学が好きな人 …
振動数方程式の導出は以下です.
この記事はこんな人にオススメです 振動や機械力学が好きな学生 機械工学を専攻している学生 振動数方程式の導出が…
実験の方法
打撃加振法
打撃加振とは,構造体をハンマーかなんかで叩くことです.
叩いた時の構造体の応答を確認する目的で行われます.
だいたい打撃加振法の実験の概略図を以下のようになると思います.
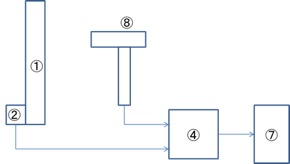 ①供試体:打撃加振の実験では,鉄棒,アルミ棒である.
①供試体:打撃加振の実験では,鉄棒,アルミ棒である.②加速度計:供試体に加えられた衝撃による振動を,加速度として計測する装置である.
④アンプ:加速度計で発生した加速度波形を増幅する装置である.
⑦FFTアナライザ:加速度データを取り込み,高速フーリエ変換することで加速度を周波数領域での観察を可能にするものである.これにより周波数応答のピーク時の周波数を数値として読み取れる.
⑧インパルスハンマー:供試体に衝撃入力を加え励振させるものである.鉄板は一端固定で定盤に固定されており,また中実鉄棒と中空アルミ棒は両端自由支持で,それぞれ糸で吊るす事を打撃試験の条件とする.
簡単な絵ですけれども,このような方法が一般的かと思います.
周期加振法
また,物体の振動特性を計測したいときには,打撃加振法だけではなく,周期的に加振を加える周期加振法というのもあります.
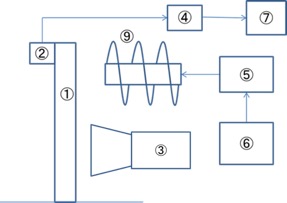
①供試体:周期加振法で用いる供試体は鉄板である.
③ストロボスコープ:供試体を照らす共振周波数と同期させた光を照射する装置である.(今回の実験では使ってませんがあると便利です.)
⑤パワーアンプ:正弦波信号を増幅させる装置である.
⑥関数発生器:正弦波信号を発生させているものである.
⑨パワーアンプ:増幅させた正弦波信号により,周期的な磁界を発生させるものである.
それぞれ添え字の機器を以下に記す.尚,②と④,⑦については,打撃加振法と一緒!
供試体の鉄板は一端固定で定盤に固定されている
こんな感じで実験を行なっていきます
固有振動数の理論値を求める
3つの供試体である,忠実鉄棒,中空アルミ棒,鉄板の固有振動数を理論的に求めていきます!
中実鉄棒編
今回は以下のような中実鉄棒を使って実験しました.
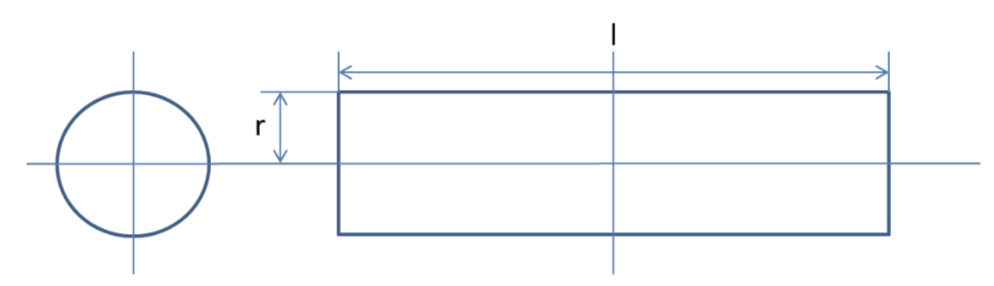
忠実鉄棒の測定値値です.

鉄棒の半径はノギスを使用し3回測定の平均を使用し,長さはスケールで一回測定しました.
それぞれだいたい5mmと353mmですね.
これは,理論値の計算のときに使います.
ちなみにヤング率Eは 軟鉄の値の211.4(Gpa),密度rは7874(kg/m3)を用います.

ここら辺は理科年表に書いてあるぞ!
以上の数値を使って,忠実鉄棒の固有振動数の理論値の計算をします.

固有振動数fmに,具体的なmの番号を代入して,それぞれ4番目まで求めてみましょう!

これで,2番目から4番目までの理論的な固有振動数が求まりました!

長くて息切れしそうだ..みんなも一緒にもう少し頑張ろうね!
中空アルミ棒編
今度は,供試体に使った中空アルミ棒も同様に理論値の振動数計算をしますが,ここは個人でやってみてください!(要望があれば計算式載せます)
それぞれの測定値は以下のようなものです.
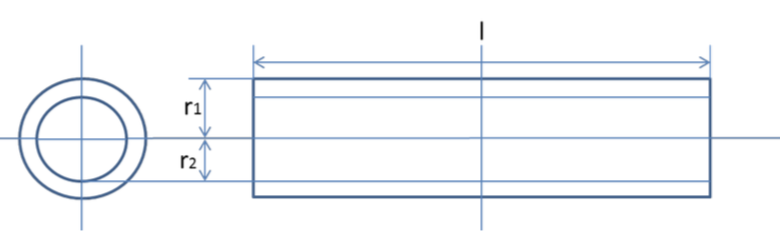
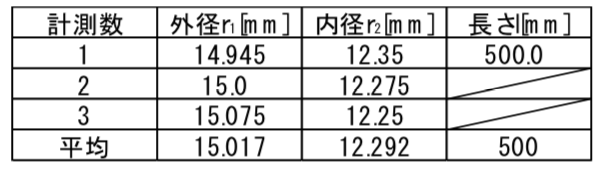
またヤング率Eは使用する材料ジェラルミンの値69.0 (Gpa),密度ρは2800(kg/m3)を用います.
おいらが計算した結果によると以下のようになりました.

鉄板編
そろそろ材料の特性については,飽きてきたと思いますが,これが最後です笑
ヤング率と密度は軟鉄の値です.
計算してみてください.

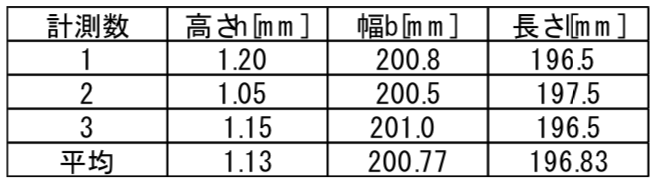
計算した鉄板の固有振動数は以下です

3つの供試体の理論値をまとめる
以上,三つの供試体の計算した理論値をまとめると以下のようになりました.
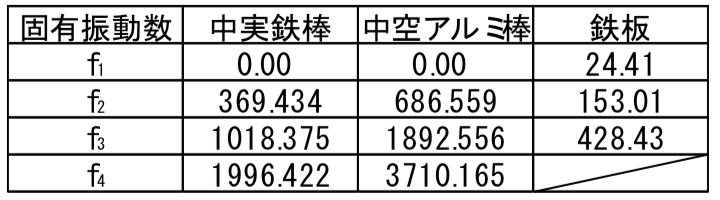
さてさて,理論値を計算したので,次回から供試体に打撃を与えて,固有振動数を実験的に計測していきましょう!!
打撃加振実験
打撃試験は,インパルスハンマーにて行います.
流れとしては,前述した打撃加振法の概要図にしたがって,以下のように行いました.
- 供試体にインパルスハンマーで加振
- アンプで増幅した加速度を計測
- FFTアナライザで高速フーリエ変換をし,周波数データの確認
- 周波数応答のピークを用いて,系の固有振動数を求めた(計測値)
- 計測値と理論値の比較
こんな感じですね.
実際に,各供試体の固有振動数の計測データを以下に示します.
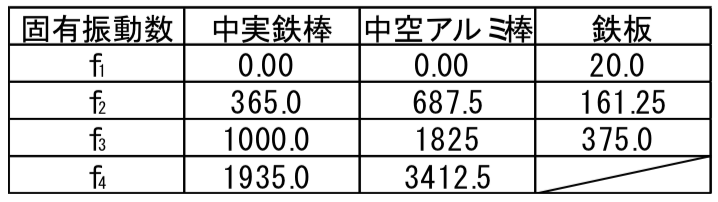
ぱっと見,理論値で導出した値とおおよそあっていることが確認できますね!
周期加振実験
周期的な加振は,関数発生器というもので行います.
具体的には,関数発生器に正弦波を発生させて,パワー・アンプによって信号を増幅させます.
その増幅させた信号を電磁石に送り,周期的な磁界を発生させることで行なっております.
この磁界によって供試体が周期的に加振されています.
この実験では,関数発生器で発生させる信号の周波数を変化させることによって,共振点を探し固有振動数を求めています.
また,同時に固有モードの観察も行なっています.

おいらが学部生の頃はこの辺,ちんぷんかんぷんだったよ
周期加振法の時の測定結果は以下になりました.

理論値と計測値を比べる
執筆がちょっと疲れてきたので,また元気があるときに続きを書きますが,理論値と実験値を比較してちょっと考えます.
打撃加振に関して
理論値と実験値を比較すると,あまりずれはないので,今回の実験は上手くいったのではないでしょうか.
打撃加振時のモデル化についてまた後ほど詳しく記載していきますが,最終的に減衰比を0と近似して算出しているのでちょっとした誤差の影響になるのでしょうか.
減衰を考えて,コンピュータで解くともう少し実験値に近ずくのかな?という感触です.
また固有振動数は,質量にも依るので,もしかしたら供試体につけた加速度センサーの質量による誤差かもしれません.
まあ,今回は,実験値とほぼ同じような値だったので良しとしておきましょう...
打撃加振法によって,固有振動数が測定できる理由は以下にまとめました.
この記事はこんな人にオススメです 機械工学を専攻している大学生 固有振動数について理解を深めたい人 振動や物理…
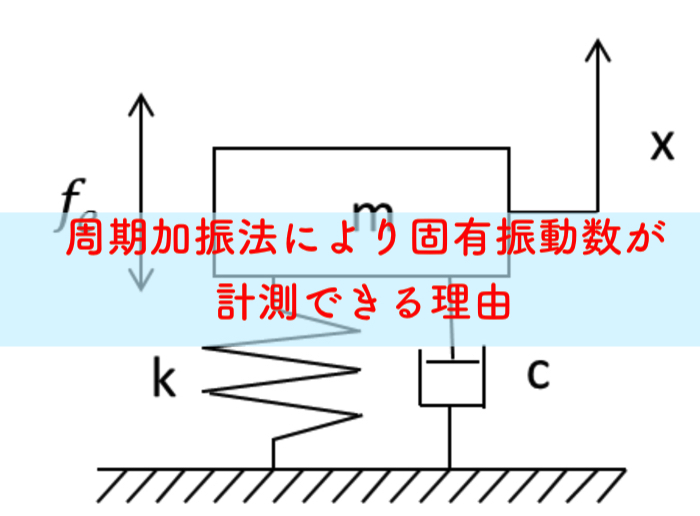
周期加振法によって,固有振動数が測定できる理由は以下にまとめました.
この記事はこんな人にオススメです 機械工学を学ぶ全ての学生 一自由度振動系を学習している方 固有振動数の導出に…
共振についても,上の記事で詳しく触れています.



仕事で振動工学の知識が必要になったので勉強のために拝見いたしました。理論と実践の両方が併記されていて非常にわかりやすかったです!