- 機械工学を学ぶ全ての学生
- 一自由度振動系を学習している方
- 固有振動数の導出について詳しく知りたい方
こんにちは.けんゆー(@kenyu0501_)です.
以前「打撃加振法により固有振動数が測定できる理由」について書きました.
この記事はこんな人にオススメです 機械工学を専攻している大学生 固有振動数について理解を深めたい人 振動や物理…
今回は,それのちょっと発展版で,周期加振法によって固有振動数が測定できる理由について一自由度振動系を用いて考えていきます.

この記事も数式ばっかだけど頑張れよな!
一自由度振動系のモデル
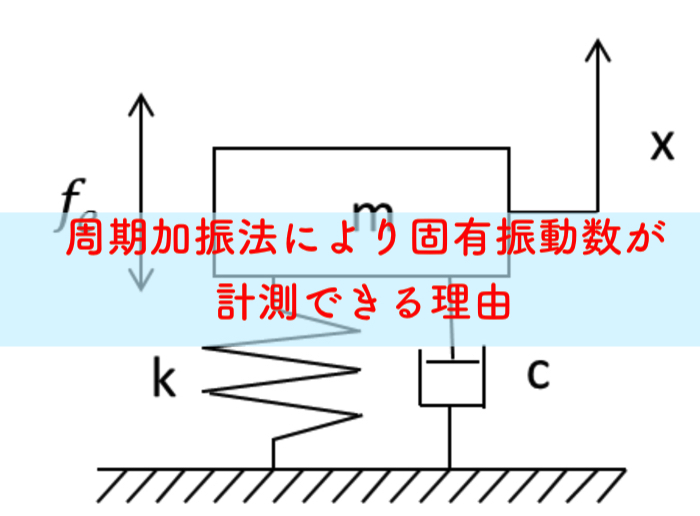
一自由度系の強制加振モデルとして,下の図のような周期加振を考えます.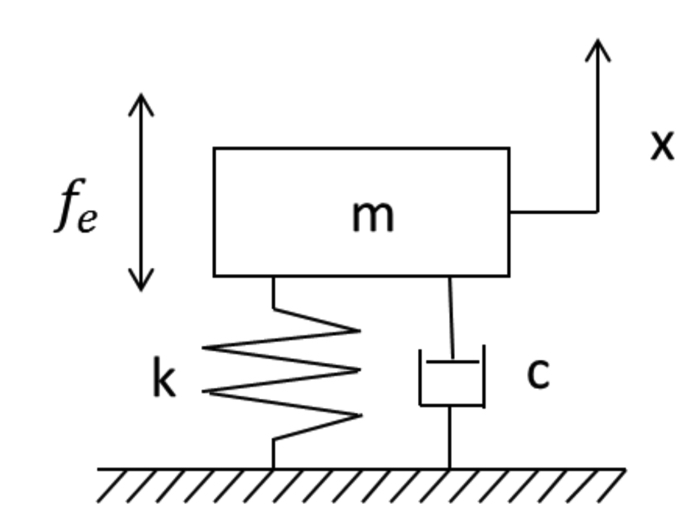
前回の打撃加振法と同様な粘性減衰を考慮したモデルを用いますが,今回は,周期加振が外力として加わっていますね.
この記事はこんな人にオススメです. 1自由度系の振動モデルを勉強している人 固有振動数の導出までを理解したい人…
今回は,周期的な加振力feが加わった系の数学的なモデルを考え,最終的に固有振動数を導出するところまで行います.
運動方程式から,固有振動数の導出
では早速,運動方程式を立てていきましょう.
バネ定数はk,減衰係数をc,質量をmとし,系は不足減衰振動の状態です.(ζ<1)


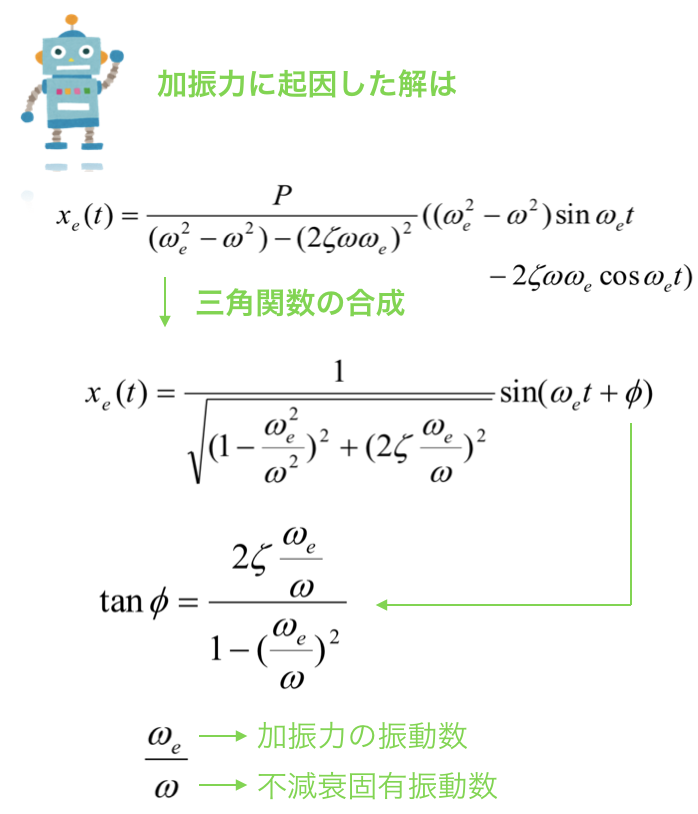



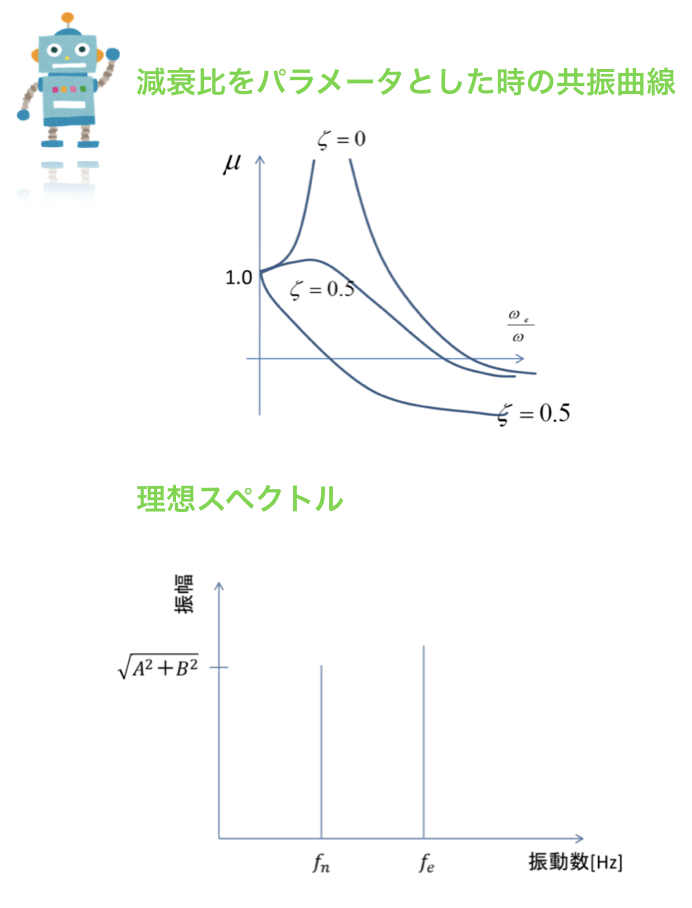
加振力の振動数ωeと,不減衰固有振動数ωとの比は,振動工学を学ぶ上で重要なものです.
この比が1に近づくと,応答振幅率μの振幅の分母がかなり小さくなるため,振幅自体がとても大きくなります.
この状態を「共振」と言います.
振動振幅が非常に大きくなるために,構造物にとってとても危険な状態になります.

共振は危険なんだね!
固有振動数の理想スペクトルについて
理想スペクトルの縦軸の振幅は,外部の力によって決定されます.
(応答振幅率μの式を見てください.)
横軸の振動数feは定常状態の時であり,外力の角振動数ωeによって決定されます.
一方で,振動数fnは同時方程式の解に依存するもので,物体の持つ固有振動数であり,十分に外力が振動に影響していない場合です.
モデル化する意義?
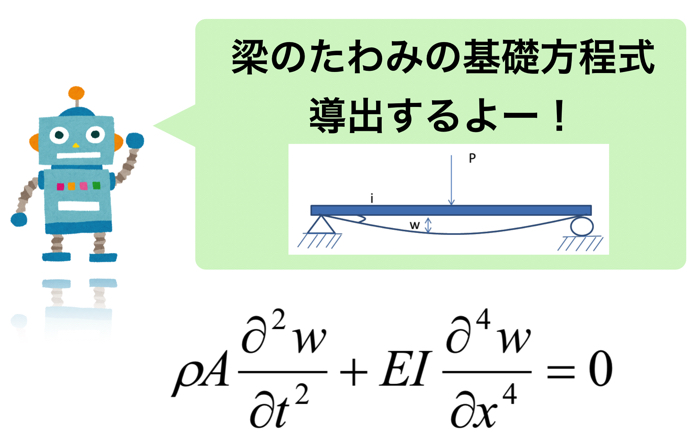
ちょっとここでは,梁をモデル化について考えていきましょう.
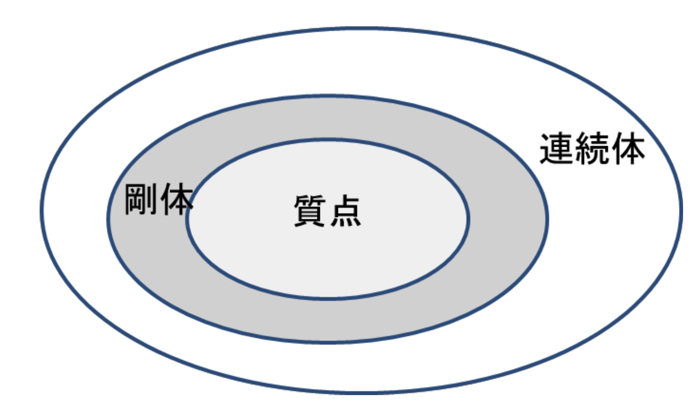
梁というのは,無限自由度の分布系(すなわち連続体)に分類されると思います.
力学モデルを構築するのに最適な自由度の数というのは,解明したい振動現象や,運動の性質に依存することになります.
そのため,モデル化をして自由度を限定するということは,見たい現象にスポットを当てた良い方法だと思います.

モデル化は見たいところ以外は妥協しないといけないよ!贅沢はだめ!
一自由度系モデルと連続体の梁の運動
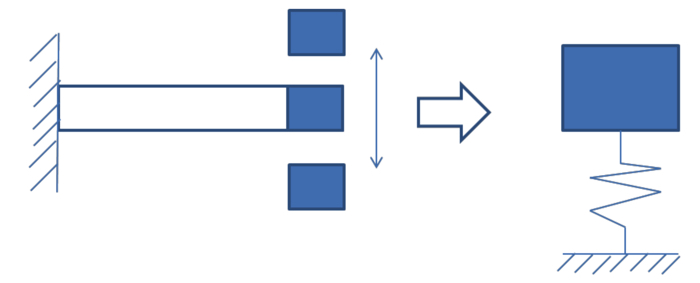
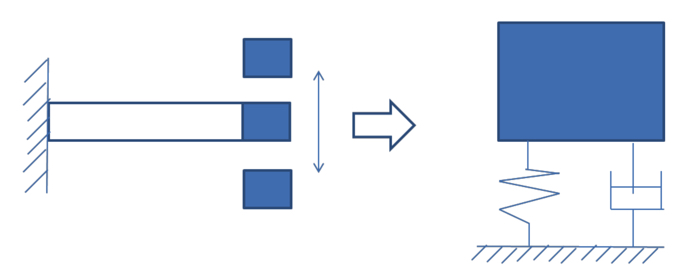
現実の連続体を一自由度系として単純化することにより,幾何学的な運動を,並進運動だけに絞って考えることができました.
連続体は自由度が高く,回転や変形も考えないといけず複雑です.
しかし,今回のように,固有振動数などの並進運動によって求めることができるパラメータに限っては,一自由度系のモデルで考えた方が楽だったりします.
ここで,一自由度系モデル長所と短所は次のようになります.
- 1つの決まった運動のみが可能で,その運動を1個の変数で完全に記述することができる
- 大体の場合,コンピュータが不要で,手計算で目的の解が求まる
- 回転や変形などの複雑な運動に対応できない
- 複雑な力,質量分布を考えていないので,誤差を含む.
みんなもモデル化するときは,この変を意識して使ってくださいね!