- 機械工学を専攻する学生
- 梁のたわみなどに興味がある人
- 振動工学が好きな人
こんにちは.けんゆー(@kenyu0501_)です.
以前,「梁や板に加振(周期,打撃)したときの固有振動数と固有モードを測定する実験」を書きました.
この記事はこんな人にオススメです 機械工学を専攻している大学生の人 物理や数学が好きな人 振動に関する分野が好…
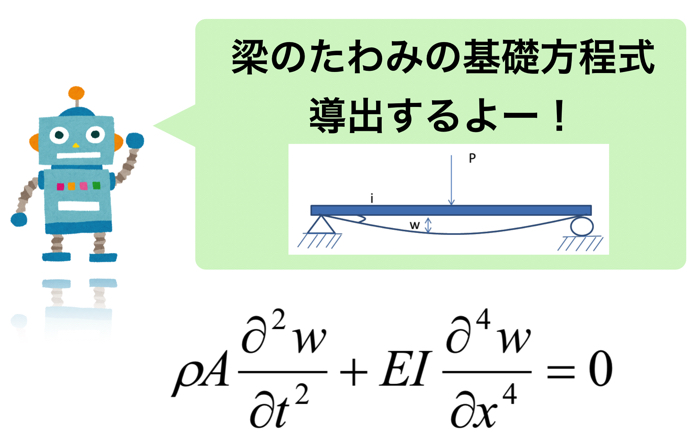
そこでは,断りもなく,以下の「梁のたわみに関する基礎方程式」
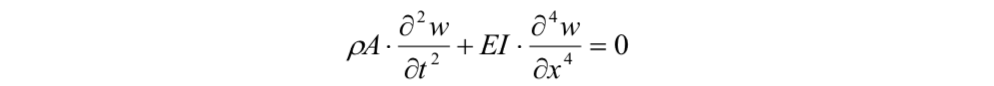
を用いていましたので,この記事では,上の式の基礎方程式を導出していきます.

では,早速やっていきましょう!!
梁のモデル図から導出
梁のたわみの基礎方程式を導出していくために,先ずは,以下のような「集中荷重Pを受けた梁のモデル」について考えていきます
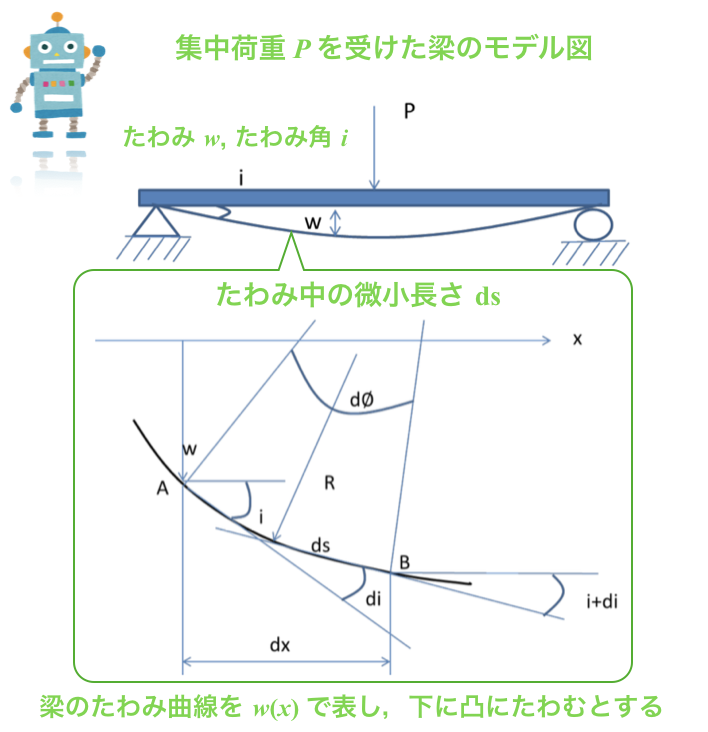
梁のたわみ曲線をw(x)で表して,上の図のように下に凸にたわんだ場合を考えています.
またdsだけ離れた点をA,Bとし,この2点の曲線上の長さをdsとします.
点Aおよび点Bでのたわみ角をiおよび,i+diとします.
曲線半径Rで,中心角dφの円弧を考えると,たわみ曲線の長さは,ds=Rdφとなります.
幾何学的関係から,同一円弧上の2点における2つの接線のなす角度は,円弧の中心角に等しいので,ds=-Rdiとなります.
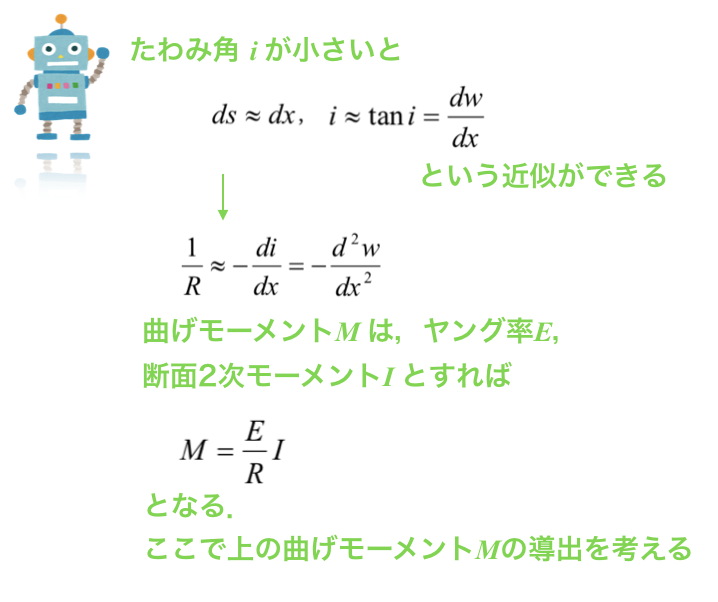
ここでは,たわみ角iが小さい場合を考えます.
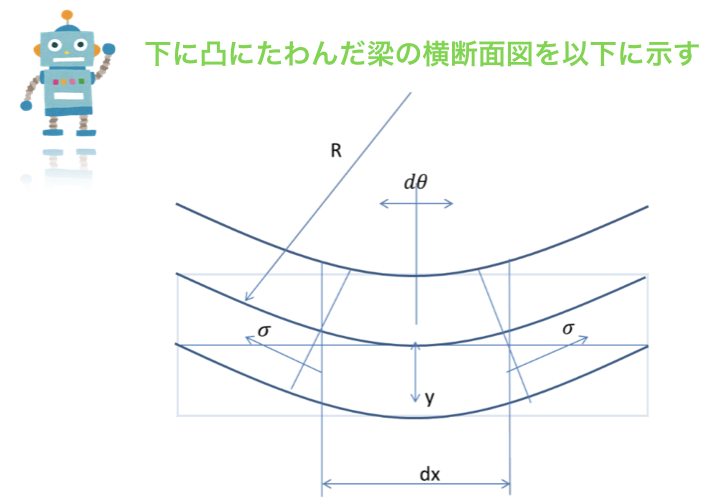
上の図では,凸側は伸びていて,凹側は縮んでいます.
また,その間に伸縮しない面が存在しているのが確認できるかと思います.
この伸縮しない面を中立面といい,その横断面との交点を中立軸といいます.
このページでは,中立軸からの距離をyとし,内部応力をσで表すことにします.


せん断力Fと曲げモーメントMの関係が出たので,以下のたわみの基礎式を導きましょう.
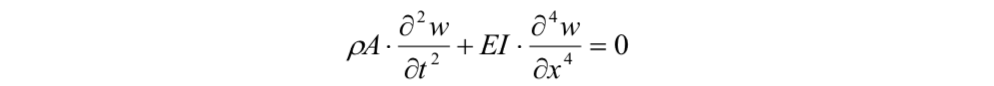
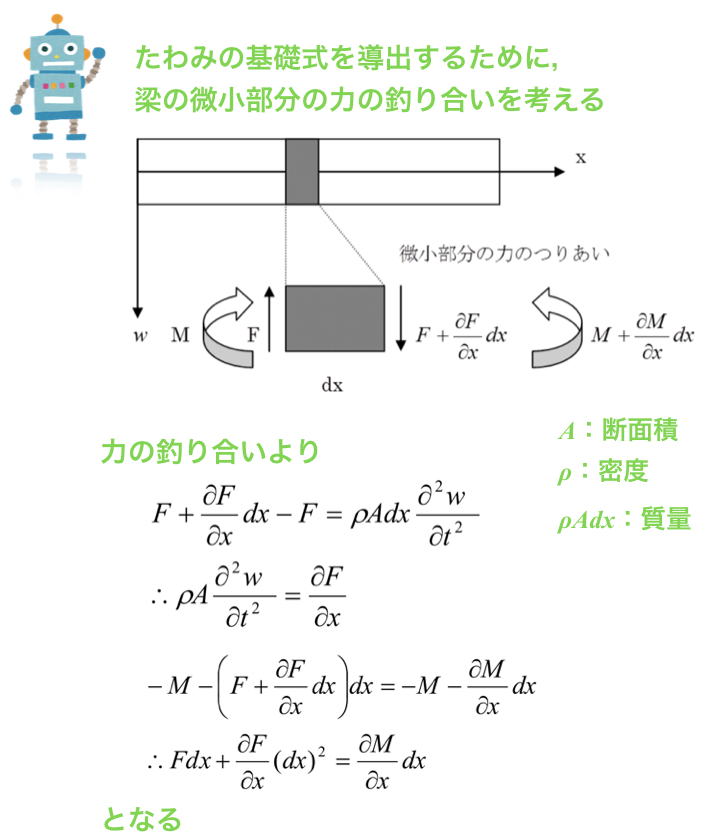
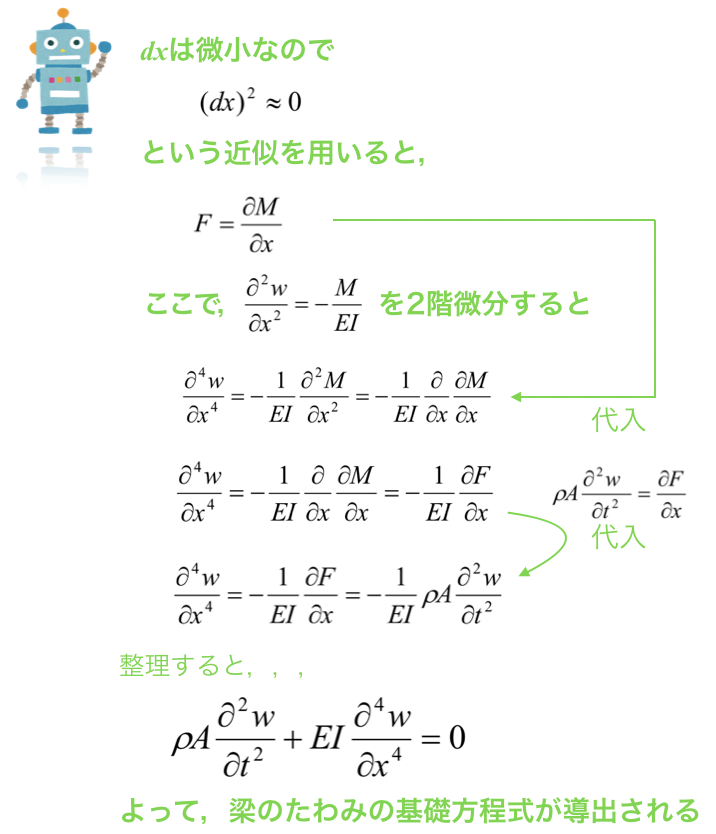
以上により,梁の導出ができました.
両端自由の振動数方程式の導出
「梁や板に加振(周期,打撃)したときの固有振動数と固有モードを測定する実験」の記事では,
この記事はこんな人にオススメです 機械工学を専攻している大学生の人 物理や数学が好きな人 振動に関する分野が好…
両端自由の条件での振動数方程式が必要になるため,次回の記事でやります.
今回導出した梁のたわみの基礎方程式から,振動数方程式の導出を行います.
ではー!