
- サポートベクターマシンSVMについて詳しく知りたい方
- 機械学習で分類や回帰などをやってみたい方
- SVMをパパッと実装してみたい方
こんにちは.
今日は機械学習の一つであるサポートベクターマシンについて書いていきます.
(ここでは,線形SVMに限って説明していきます)
分類とか回帰などの問題を解くときに使われる手法で,1960年代からある手法です.
ここでは,サポートベクターマシンがどのようなものなのかを説明して,実際にPythonを使ってプログラムを組んでいきます.
サポートベクターマシンSVMとは
話を簡単にするために,2次元の2つのクラスに分類する絵で説明します.
(線形サポートベクターマシンと言います)

SVMとは,クラスを明確に分ける境界線を引くための手法です.
上の図の例では,赤と青のクラスを明確に分ける境界線を引いてますね.

明確に,赤と青の場所の決めているんだね!これで,もし赤か青か分からないデータが来たときには,どっちのクラスに属するか一目瞭然なんだね
ここで,上の特徴量としては2つ(2次元)なので「線」を引きますが,3次元になると「面」を引きます.
数学的に線形の場合,「直線」や「平面」の一般化として超平面という概念があるために,n次元(任意の次元)に対して求まる境界を超平面と言います.
| 特徴量の次元 | 境界の種類 |
|---|---|
| 2次元 | 直線 |
| 3次元 | 平面 |
| n次元 | 超平面 |
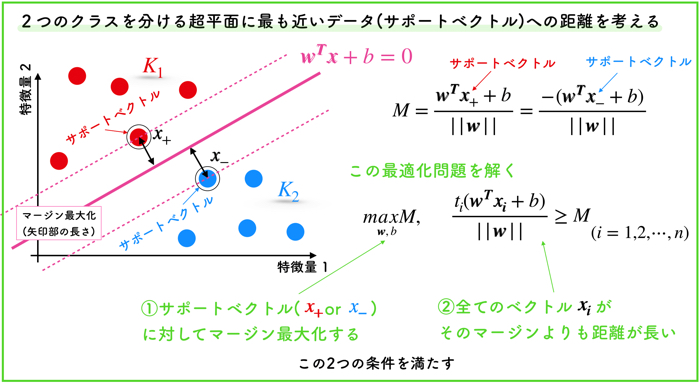
超平面の定め方はマージン最大化
例えば,上の2クラスのデータを分離する境界線の引き方は無限にあると思いますが,SVMでは「マージン最大化」という方法で線を引きます.
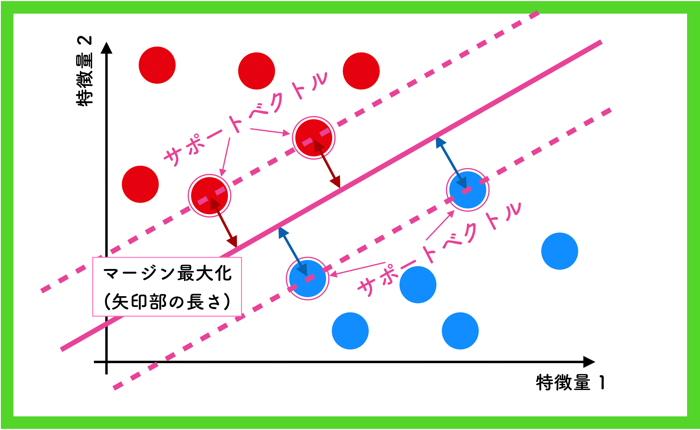
マージンというのは「余白」を意味する言葉ですが,境界からもっとも近いベクトル(特徴量も持った点)との距離を表します.
上の例の場合は,赤と青のクラスからもっとも近いベクトルを2点ずつ選んで,そのマージンを最大にするように線を引いてます.
この選ばれたベクトルをサポートベクトルと呼びます.
つまり,マージンを最大化することは,赤のクラスからも青のクラスからももっとも遠い境界を引くということを意味しています.
一度境界を定めると,サポートベクターマシンを使った「分類器」が完成します.
この分類器に対して,特徴量1と2を持つ新しいデータを入力したときに,赤のクラスと青のクラスのどちらかに属するか判別することが可能です.
しっかりとした理論的な説明を知りたい人は,以下をご覧ください.
この記事はこんな人におすすめです. サポートベクターマシンの理屈を詳しく理解したい人 機械学習の勉強をしている…
必要な前提:線形分離可能であること
SVMでマージン最大化するにあたって,必要な前提があります.
それは,データが線形分離可能であることです.
すなわち,二つのクラス(例だと赤か青か)を持つデータでなければいけません.
メリット:計算コストが小さい
このSVMには計算コストが小さいというメリットがあります.
線形分離可能であるデータに対して,境界を引くときに必要なデータはサポートベクトルだけだからです.
サポートベクトル以外の点は,境界を引くのに関係がありません.
(すなわち,計算しなくても良い)
理論的な解説はスライド資料へ
Pythonプログラムについて
今回は,Pythonを使ってSVMの実装をしていきます.
分類するのに使うデータはおいらが研究で使用している脳波データです.
プログラムについて
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 | # -*- coding: utf-8 -*- from sklearn import svm import numpy as np import matplotlib.pyplot as plt from matplotlib.colors import ListedColormap from mpl_toolkits.mplot3d import Axes3D from operator import itemgetter #ファイル名宣言(教師データteach.txtとテストデータtest.txt読み込み) inputData_teach = 'teach.txt' inputData_test = 'test.txt' #教師データとでテストデータをロードし、それぞれの変数に格納する p_teach = np.loadtxt(inputData_teach, delimiter='\t', dtype='float') p_test = np.loadtxt(inputData_test, delimiter='\t', dtype='float') # 特徴量のセットを変数Xに、クラスを変数yに格納 X = p_teach[:,1:4] y = p_teach[:, 5] y = y.astype(np.int64) x_test = p_test[:,1:4] y_test = p_test[:, 5] y_test = y_test.astype(np.int64) # サポートベクトルマシン clf = svm.SVC(C=1.0, kernel='linear') # フィッテング clf.fit(X, y) # 0,1の予測をRに格納 R = clf.predict(x_test) # 以下はグラフの描写 # グラフ表示エリアとする x_min = min(X[:,0]) - 1 x_max = max(X[:,0]) + 1 y_min = min(X[:,1]) - 1 y_max = max(X[:,1]) + 1 # グラフ表示エリアを縦横500ずつのグリッドに区切る # (分類クラスに応じて背景に色を塗るため) XX, YY = np.mgrid[x_min:x_max:500j, y_min:y_max:500j] ZZ = (clf.coef_[0][0]*XX + clf.coef_[0][1]*YY + clf.intercept_)/ -clf.coef_[0][2] XX_line = XX[:,0] YY_line = YY[0,:].T ZZ_line = np.diag(ZZ) fig = plt.figure(figsize=(18,16)) ax1 = plt.subplot2grid((2,4), (0,0), projection='3d') ax2 = plt.subplot2grid((2,4), (0,1)) ax3 = plt.subplot2grid((2,4), (1,0)) ax4 = plt.subplot2grid((2,4), (1,1), sharex = ax2, sharey = ax3) ax5 = plt.subplot2grid((2,4), (0,2), projection='3d') ax6 = plt.subplot2grid((2,4), (0,3)) ax7 = plt.subplot2grid((2,4), (1,2)) ax8 = plt.subplot2grid((2,4), (1,3), sharex = ax6, sharey = ax7) # グラフ1の設定 # 軸ラベルを設定 ax1.set_xlabel('A') ax1.set_ylabel('B') ax1.set_zlabel('C') # ターゲットに応じた色付きでデータ点を表示 # relax (y=0) のデータのみを取り出す Xc0 = X[y==0] # stress (y=1) のデータのみを取り出す Xc1 = X[y==1] # relax の学習用データXc0をプロット ax1.scatter(Xc0[:,0], Xc0[:,1], Xc0[:,2], c='c', linewidths=0.5, edgecolors='black') # stress の学習用データXc1をプロット ax1.scatter(Xc1[:,0], Xc1[:,1], Xc1[:,2], c='m', linewidths=0.5, edgecolors='black') ax1.plot_surface(XX, YY, ZZ, rstride=8, cstride=8, alpha=0.3) # グラフ2の設定 ax2.scatter(Xc0[:,0], Xc0[:,1], c='c', linewidths=0.5, edgecolors='black') ax2.scatter(Xc1[:,0], Xc1[:,1], c='m', linewidths=0.5, edgecolors='black') #ax2.plot(XX_line, YY_line, alpha=0.3) # グラフ3の設定 ax3.scatter(Xc0[:,1], Xc0[:,2], c='c', linewidths=0.5, edgecolors='black') ax3.scatter(Xc1[:,1], Xc1[:,2], c='m', linewidths=0.5, edgecolors='black') #ax3.plot(YY_line, ZZ_line, alpha=0.3) # グラフ4の設定 ax4.scatter(Xc0[:,0], Xc0[:,2], c='c', linewidths=0.5, edgecolors='black') ax4.scatter(Xc1[:,0], Xc1[:,2], c='m', linewidths=0.5, edgecolors='black') ax4.plot(XX_line, ZZ_line, alpha=0.3) # グラフ5の設定 # relax (y=0) のデータのみを取り出す xt0 = x_test[y_test==0] # stress (y=1) のデータのみを取り出す xt1 = x_test[y_test==1] # relax のテストデータをプロット ax5.scatter(xt0[:,0], xt0[:,1], xt0[:,2], c='b', linewidths=0.5, edgecolors='black') # stress のテストデータをプロット ax5.scatter(xt1[:,0], xt1[:,1], xt1[:,2], c='y', linewidths=0.5, edgecolors='black') ax5.plot_surface(XX, YY, ZZ, rstride=8, cstride=8, alpha=0.3) # 予測とターゲットが合致したデータのみを取り出す x_true = x_test[y_test==R] # 予測とターゲットが合致した点に対して、赤い枠線を表示 ax5.scatter(x_true[:,0], x_true[:,1], x_true[:,2], c=(0, 0, 0, 0), linewidths=1.0, edgecolors='red') # グラフ6の設定 ax6.scatter(xt0[:,0], xt0[:,1], c='b', linewidths=0.5, edgecolors='black') ax6.scatter(xt1[:,0], xt1[:,1], c='y', linewidths=0.5, edgecolors='black') ax6.scatter(x_true[:,0], x_true[:,1], c=(0, 0, 0, 0), linewidths=1.0, edgecolors='red') #ax6.plot(XX_line, YY_line, alpha=0.3) # グラフ7の設定 ax7.scatter(xt0[:,1], xt0[:,2], c='b', linewidths=0.5, edgecolors='black') ax7.scatter(xt1[:,1], xt1[:,2], c='y', linewidths=0.5, edgecolors='black') ax7.scatter(x_true[:,1], x_true[:,2], c=(0, 0, 0, 0), linewidths=1.0, edgecolors='red') #ax7.plot(YY_line, ZZ_line, alpha=0.3) # グラフ8の設定 ax8.scatter(xt0[:,0], xt0[:,2], c='b', linewidths=0.5, edgecolors='black') ax8.scatter(xt1[:,0], xt1[:,2], c='y', linewidths=0.5, edgecolors='black') ax8.scatter(x_true[:,0], x_true[:,2], c=(0, 0, 0, 0), linewidths=1.0, edgecolors='red') ax8.plot(XX_line, ZZ_line, alpha=0.3) plt.savefig('a_100mass_D0_4Hz_linear.png') # 描画したグラフを表示 plt.show() |
使うデータについて
teach.txtとtest.txtのファイルの構造は以下のようになっています.
| No | 特徴量1 | 特徴量2 | 特徴量3 | 特徴量4 | クラス(0 or 1) |
|---|---|---|---|---|---|
| 1 | 〇〇 | 〇〇 | 〇〇 | 〇〇 | 0 |
| 2 | 〇〇 | 〇〇 | 〇〇 | 〇〇 | 0 |
| ・・・ | ・・・ | ・・・ | ・・・ | ・・・ | ・・・ |
| 61 | 〇〇 | 〇〇 | 〇〇 | 〇〇 | 1 |
| 62 | 〇〇 | 〇〇 | 〇〇 | 〇〇 | 1 |
| ・・・ | ・・・ | ・・・ | ・・・ | ・・・ | ・・・ |
0列目は,ベクトル個数のナンバリング(No)です.
1列目から4列目までは,それぞれの特徴量を表すデータが入ってます.
スカラー量ですね.
最後の5列目は,その状態を0か1かで格納してます.
ここでは,「0:リラックス時の脳波データ」,「1:ストレス時の脳波データ」という形で状態を保持しています.
おいらの場合は,脳波の時系列のデータからある処理を行って,特徴量を4つ抜き出して,リラックスかストレスかの状態分けをしてます.
ここの特徴量の設計の部分は人間はやらないといけない部分です.
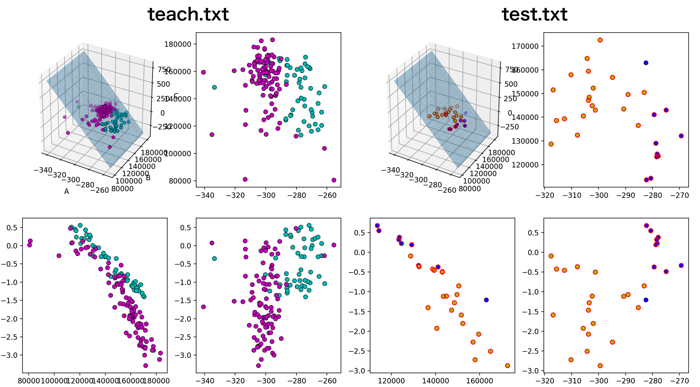
例えば,上の特徴量1から3を使ったデータを可視化すると以下のようになります.
(記載しているプログラムも,特徴量1~3を使ってSVMを回しています)
データの抜き出しと変数への格納
上のデータの抜き出しと格納は以下のように行ってます.
1 2 3 4 5 6 7 8 | # 特徴量のセットを変数Xに、クラスを変数yに格納 X = p_teach[:,1:4] y = p_teach[:, 5] y = y.astype(np.int64) x_test = p_test[:,1:4] y_test = p_test[:, 5] y_test = y_test.astype(np.int64) |
p_teach[ : , 1:4 ]と書くと,1列目から3列目までが抜き出されます.
これをベクトルの変数Xに格納してます.
(特徴量ですね)
3列目までなので,気をつけてください.
クラスの状態(0 or 1)は,変数yに格納です.
これは,5列目なので,p_teach[ : , 5]という風に書きます.
「:」がない場合,列指定になるので,これで,各ベクトルに対するクラスの指定ができました
testデータも同様に行います.
サポートベクターマシンは3行でかける
サポートベクターマシンSVMは,サイキットラーン(Scikit-learn)のライブラリを使います.
ここで,サイキットラーン(Scikit-learn)は機械学習をするときに,便利なライブラリで色々な機能が入っているのでオススメです.
Scikit-learnをお使いのパソコンに入れてください.
インストールが終わると,プログラムの初めに,以下の定義をしてください.
これでSVMが使えます.
1 | from sklearn import svm |
SVMは,Scikit-learnを使用して,以下の3行で書くことができます.
1 2 3 4 5 6 | # サポートベクトルマシン clf = svm.SVC(C=1.0, kernel='linear') # フィッテング clf.fit(X, y) # 0,1の予測をRに格納 R = clf.predict(x_test) |
ここで,svm.SVC( )で,サポートベクターマシンによる分類器を呼び出して,clfという変数に一度格納しておきます.
内側のパラメータであるCとKernelはそれぞれ,ペナルティ寄与,サポートベクターマシンのタイプです.
ペナルティ寄与Cとは,境界を決める時のペナルティの寄与の大きさです.
Cが大きいほど,誤認識された点へのペナルティが大きくなります.
(このへんは,ハードマージンという概念が必要ですが,話がややこしくなるので飛ばします.)
デフォルトの「C=1.0」でも十分分類できるので,取っ掛かりとしてはそれで大丈夫です.
「kernel=’linear’」は線形のサポートベクターマシンを利用するということです.
(他にも「kernel=’rbf’」という動径基底関数というものもあります.)
「clf.fit(X, y)」で,分類器に特徴量のデータとクラスの状態が渡され,境界を作ります.
最後に,「R = clf.predict(x_test)」で,テストデータを入れて,分類器が上手く機能しているか確認をしています.
詳しく知りたい方は,Scikit-learnのオフィシャルサイトへどうぞ
ではー!皆さんも楽しいSVMライフを!
SVMを実践に使いたい人へのオススメ図書です.






初めまして!
私も研究でSVMを用いることになり,こちらの記事を読ませていただきました.
とても分かりやすかったです.
ありがとうございました!
ありがとうございます.
Youtubeのチャンネルでも紹介しているので,もし良かったらご覧くださいー!
https://youtu.be/TNOC0vyIL-g
SVMを勉強するにあたって、参考にさせていただきました!
実際に実務として使うことが想定されているものでとても参考になりました!
一点わからないことがあったので、質問させていただきました。
X = p_teach[:,1:4]
y = p_teach[:, 5]
のところで、今回のデータセットでは特徴量が4つあるのですが、
<p_teach[ : , 1:4 ]と書くと,1列目から3列目までが抜き出されます.>
と記述があります。
これは、今回のSVMでの分類では4列目の特徴量は使用しないということでしょうか?
ご回答いただけると幸いです。
よろしくお願いします
お役に立てて嬉しいです。
ご質問の回答ですが、4列目は使用しておりません。
同じ脳波の研究をしている学部4年の者です。けんゆーさんの”脳波の時系列のデータからある処理を行って,特徴量を4つ抜き出して”の操作について、どのような特徴量を取ってきているのか気になります。もう少しだけ詳しくお聞かせいただけないでしょうか。よろしくお願いします。