- G検定対策をしている人
- 探索木について詳しく知りたい人
- 「幅優先探索」や「深さ優先探索」を直感的に理解したい人
こんにちは.
今回は,第1次AIブームの火付け役となった探索や推論に関しての技術で「探索木」というものの考え方について取り上げます.
人工知能(AI)は2回の冬を経て3度のブームが来ているのでしたね.
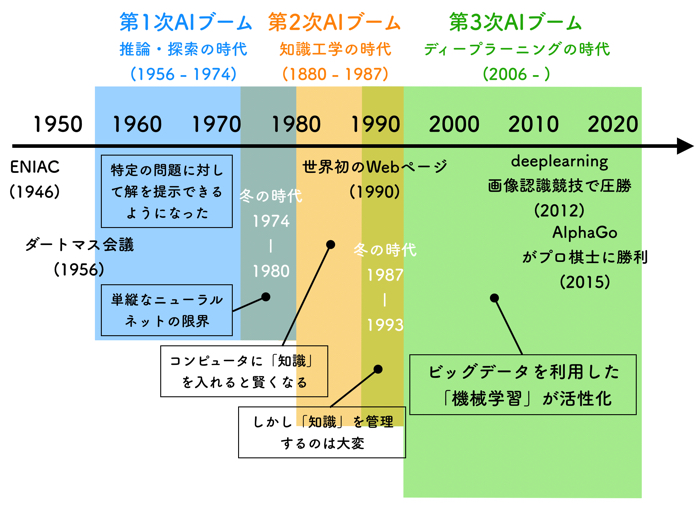
詳しく知りたい方は,人工知能の歴史をご覧ください.
この記事はこんな人にオススメです JDLA (日本ディープラーニング協会)のG検定対策をしている方 人工知能に…
今日はその第1次AIブームに関してのお話です.
なお,この時代に注目された研究の一部は,現在もなお引き続き研究され色んなところで活用されています.
迷路を考えて直感的に理解する
第1次AIブームでは,「探索」や「推論」の研究が進みました.
その結果,特定の問題に対しては解が求まるようになったのです.
「探索」の中でも基本的な手法として,「幅優先探索」と「深さ優先探索」というものがあるので,迷路の実例を取り上げて説明していきます.
迷路の例
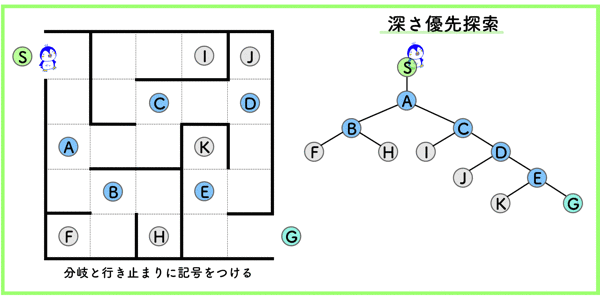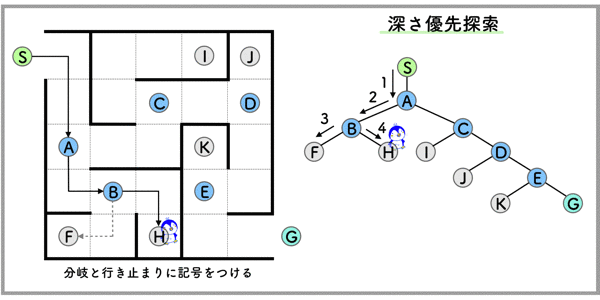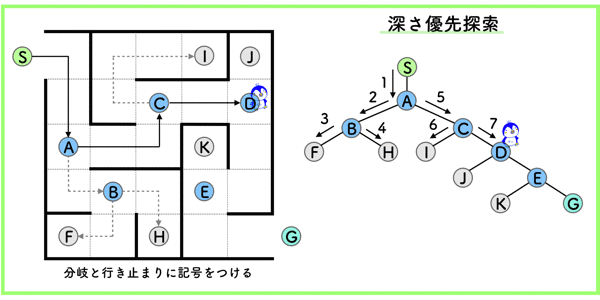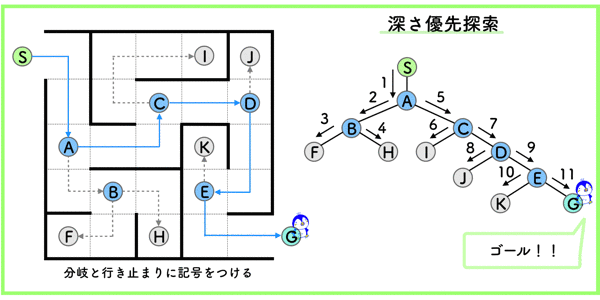
以下の図(左上)のような迷路を考えます.
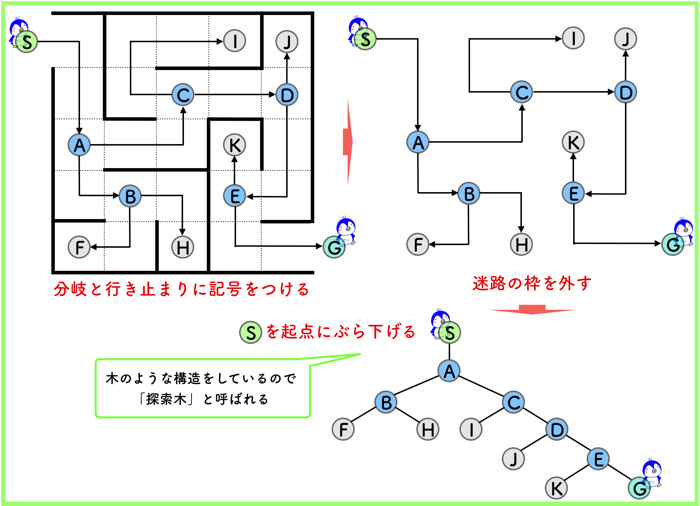
この迷路をスタート(S)からゴール(G)までの経路を探索します.
コンピュータで問題を解くために,コンピュータが処理できる形式に変更します.
- 分岐と行き止まりに記号((A)〜(K))をつける.
- 迷路の枠を取りさらう.
- スタート(S)を起点に全体をぶら下げる.
- (S)から追いかけて(G)をたどる経路を探索する
このような処理を行います.
(S)を起点にして全体をぶら下げてみると,木のような構造になっているので,探索木と呼ばれています.
探索木とは場合分けのことです.
コンピュータは繰り返し計算が非常に得意なので,こういった場合分けの問題が得意です.
場合分けによっていつかはゴール(G)にたどり着きますが,探索にかかる時間は手法によって異なります.
今回は,以下の二つの手法を紹介します.
- 幅優先探索
- 深さ優先探索
幅優先探索
直感的な理解をするために,以下の動画をご覧ください.
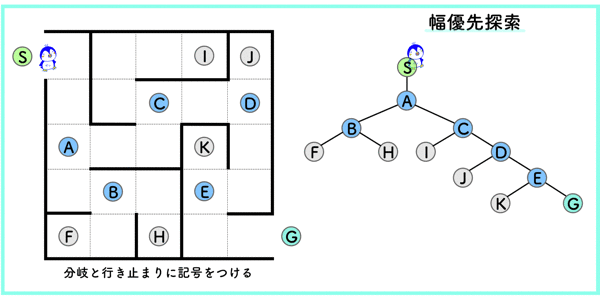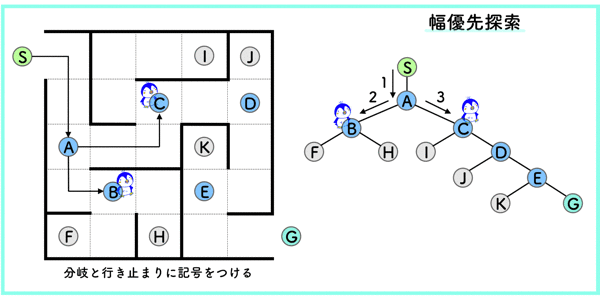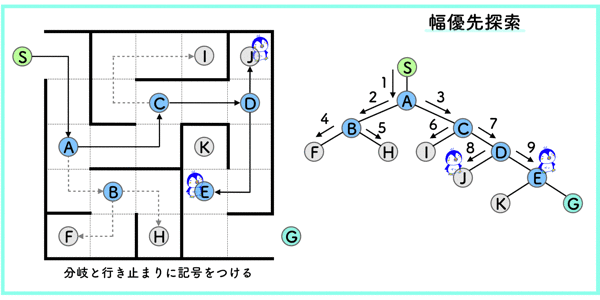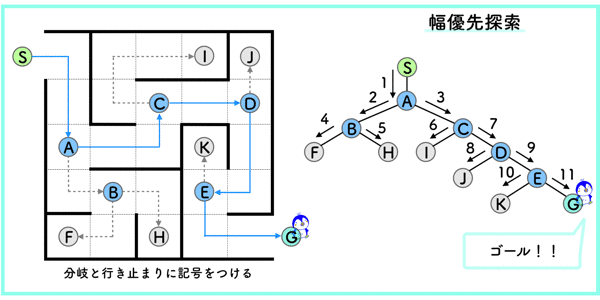
幅優先探索では,あるノードから隣接している全てのノードを探索するというシンプルな方法です.
影分身的に探索を行うので,最短距離でゴールにたどり着くことができます.
しかし,影分身をするので,複雑な迷路になるとメモリ不足で処理ができない場合があります.
(探索の途中で立ち寄ったノードの情報を全て記憶しておかないといけない)
深さ優先探索

もう一つは,深さ優先探索です.
あるノードから,行き止まりのノードまで突っ走り,行き止まりにぶつかったら,1つ手前の分岐ノードまで戻って次の行き止まりまで探索を行うというシンプルな方法です.
この場合,解が見つからなければ,もう一つ手前に戻って探索をし直すので,メモリはあまり使いません.
(ノードの情報を全て記憶しておかなくても良い)
メモリはあまり使いませんが,ゴールしたとしても,それが最適な解であるとは限りません.
運によっては早くゴールできますし,ものすごく時間のかかる場合もあります.
「幅優先選択」と「深さ優先選択」はどちらの方法もメリット・デメリットがあるので,実際には,お互いのメリットを組み合わせて探索をするなどする方が良いです.
もっと詳しく知りたい方は,以下をご覧ください.
深層学習教科書 ディープラーニング G検定(ジェネラリスト) 公式テキスト
次回は,第2次AIブームで中心的な役割をした知識表現の方に入っていきます.

またねー!
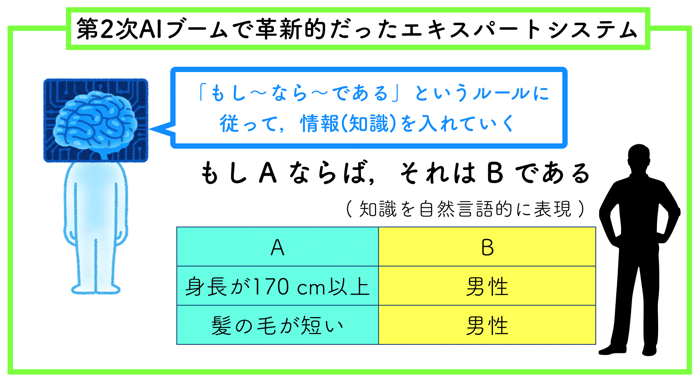
この記事はこんな人にオススメです G検定を控えている人 人工知能について詳しく知りたい人 エキスパートシステム…