- SVMを使えるだけではなく,きちんと理解したい人
- SVMを解く最適化問題に使われている特殊な変形を理解したい人
- ラグランジュの未定乗数法を理解したい人
こんにちは.けんゆー(@kenyu0501_)です.
前回,前々回までで,線形サポートベクターマシンの定式化を終えました.

詳細が気になる人はこちらを見てください.
この記事はこんな人におすすめです. サポートベクターマシンの理屈を詳しく理解したい人 機械学習の勉強をしている…
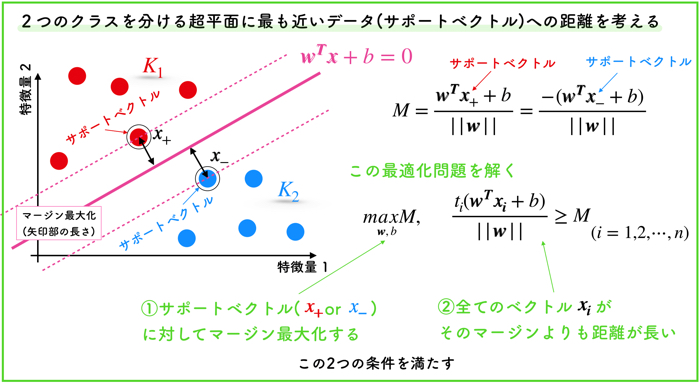
(これらの最適化問題を主問題と呼んだりします)
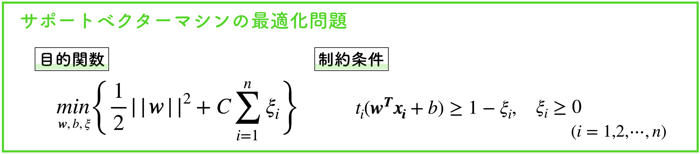
しかしながら,SVMを使う多くの場合では,上記で示したような主問題を直接的に解くことはしません.
ほとんどの場合は,主問題を「双対問題」として置き換え,別の解きやすい形で表現した問題を解きます.
そこで今日は,双対表現について考えていきたいと思います.
「主問題」 → 「双対表現」にするメリット
双対表現にするメリットとして,以下の2つがあります.
- 変数を減らすことができる.
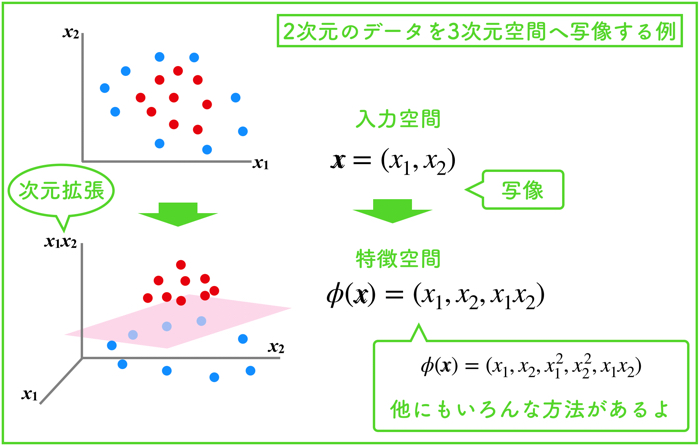
- カーネル関数が使用でき,非線形データの分類ができる.
どちらのメリットも計算コストが下がるので,SVM的にとてもありがたいのです.
では,双対表現とは,どのような形にするものなのでしょうか.
SVMの双対表現でよく使用される「ラグランジュの未定乗数法」を説明していきます.
ラグランジュの未定乗数法とは
ラグランジュの未定乗数法は,「制約付き最適化問題の代表的な解法」です.
これは,SVMを解く際に非常に重要なものになります.
なぜなら,SVMは,制約条件のついた最適化問題だからです.
しかし,この制約条件って,色々とめんどくさいのでできれば制約条件を付けたくはありません.

計算する際に,厄介なのだ!
そのため,ラグランジュの未定乗数法では,もとの最適化問題の目的関数を修正して,制約条件のない最適化問題に変形します.
ラグランジュの未定乗数法は以下です.
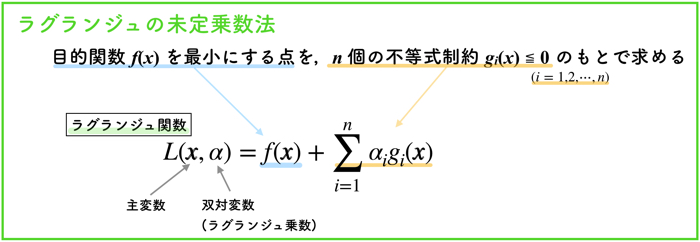
目的関数f(x)と,不等式制約g(x)にラグランジュ乗数αを掛けて,それぞれを足したものをラグランジュ関数L(x,α)と言います.
このラグランジュ関数を解くことで,制約条件付きに最適化問題を解くことに置き換えることができます.
ラグランジュ関数の導出は以下のステップの通りです.
- おのおのの制約条件の式に対して定数(ラグランジュ乗数)を用意
- これらを線型結合して新しい目的関数(ラグランジュ関数)を得る
そして,このラグランジュ関数は以下の4つを求めることで,解(x,α)を求めることが可能です.

例題で具体的な解法をみる
ちょっと式がややこしいと思うので,具体的な例題を確認して,ラグランジュの未定乗数法を理解しましょう.
ちなみに,例題は,工学のための最適化手法入門から抜粋しました.

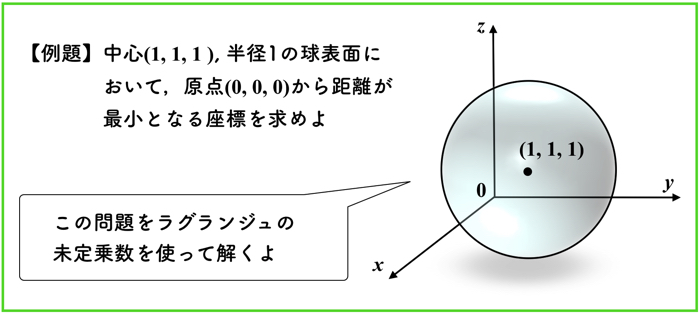
【例題】中心(1,1,1),半径1の球表面において,原点(0,0,0)から距離が最小となる座標を求めよ.

目的関数と制約条件から,ラグランジュ関数を作ります.
ラグランジュ関数の形にすると,制約条件が消えます.
そうすると,主変数と双対変数に関する偏微分を解くことによって,解が求まります.

最終的な(x,y,z)が導出できたと思います.
その値が,目的関数を最小化するときの(x,y,z)の組み合わせです.
ラグランジュの未定乗数法をSVMに当てはめて双対問題を解く
ラグランジュの未定乗数法を用いて,SVMの主問題を変形した形を双対問題といいます.
双体問題は,冒頭で出てきましたね!
さて,それで
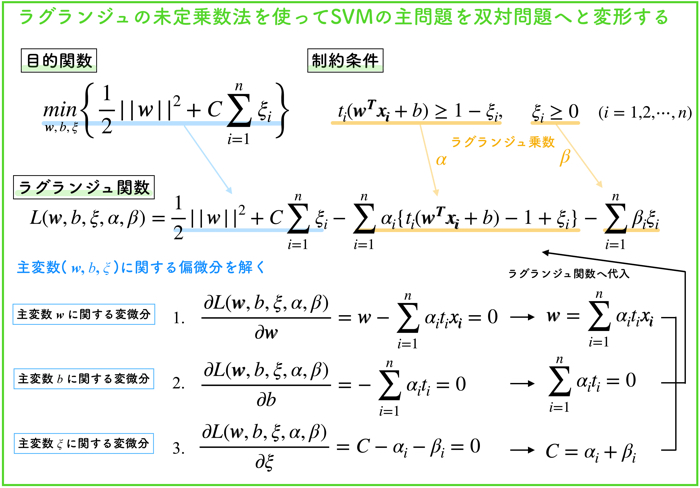
詳細な計算は飛ばしますが,ラグランジュ関数を導出して,主変数(w,b,ξ)に関する偏微分=0を解きます.
それぞれ3つの連立方程式(条件式)をラグランジュ関数に代入して整理すると,αのみの形に変形することができます.

ラグランジュの未定乗数法をもちいることによって,サポートベクターマシンの最適化問題を以上のようなαのみの関数に置き換えることができます.
これを解くことによって解が求まります.
つまり,主問題から双対問題に置き換えることによって,変数を減らすことができました.
(ラグランジュ乗数のαのみ)
かなり便利な方法ですよね.
カーネル法の導入に関しては,こちらの記事に書いてます.
この記事はこんな人にオススメです カーネル法を用いたサポートベクターマシンの解法を知りたい方 機械学習を使った…
ではー!