- カーネル法を用いたサポートベクターマシンの解法を知りたい方
- 機械学習を使った研究を行なっている方
- 非線形な分離を行う際の方法を知りたい方
こんにちは.けんゆー(@kenyu0501_)です.
前回は,サポートベクターマシンの主問題を解くためにラグランジュの未定乗数法を用いて,双対表現にしました.
双対問題にすることによって,変数を下げることができましたね!
 詳しくはこちらのページから!
詳しくはこちらのページから!
この記事はこんな人にオススメです SVMを使えるだけではなく,きちんと理解したい人 SVMを解く最適化問題に使…
今回の記事では,線形分離ができないデータに対して,どのように分離するのか,ということを書いていきたいと思います.
解説動画出しました
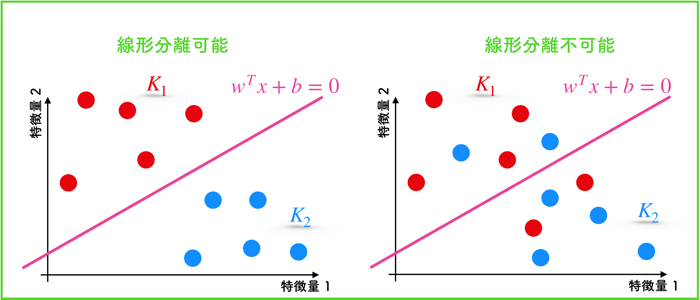
線形分離できないデータとは!?
SVMで色々とデータの分類をするときに,単純な直線(直平面)で分類ができない場合があります.
右下のようなデータですね.
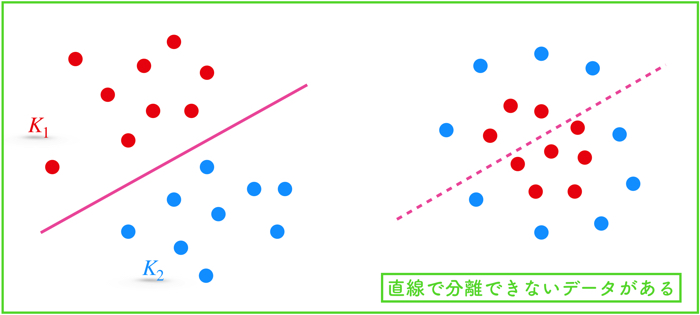
そうなった時に,元のデータを2乗とか3乗とかして,新しい特徴量データとして作り直すことで,非線形の分類が可能になったりします.
以下のような形で高次元空間への拡張を行うのですね!
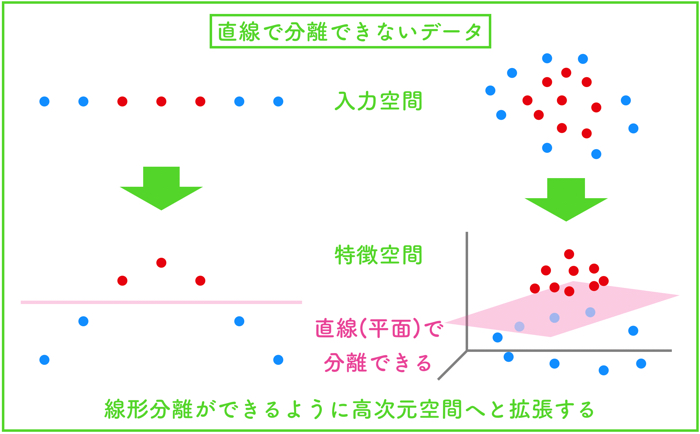
つまり,線形分離できない場合は,以下のような工夫によって分類を試みます
- 1次元のデータを2次元に拡張する
- 2次元のデータを3次元や4次元,N次元に拡張する
基本的に,そのデータが持っている特徴量の次元よりも高い次元へ拡張することになります.
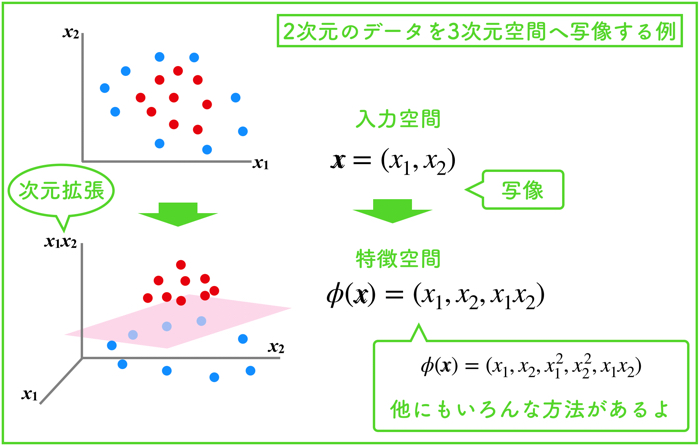
写像:高次元空間への拡張
この高次元空間への拡張のことを写像と言います.
元のデータの持つ特徴量をあらゆる形で組み合わせて,新しい特徴量で表現されたデータのこと
具体的にどのような形か例題を見ていきましょう.

xのデータを,φ(x)という新たな関数を通して,3次元まで拡張しました.
3次元目のデータをどのように作るのかというと,x1とx2をそれぞれ掛け合わせる(x1x2)ことで3次元目のデータを作成しました.
以上の例題をもとに,写像の一般化を行います.
一般に,入力空間でn次元であるデータは,高次のr次元の特徴空間へ変換する関数は以下のようになります.
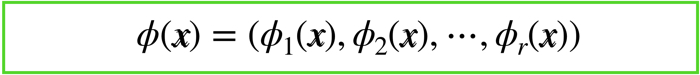
ベクトルφというのは,φという関数の集まりです.
つまり,φというのは元のデータであるx1やx2を組み合わせて新たに特徴量を作るための関数になります.
このような関数を通してできた新たな特徴量を用いることで,線形モデルでも,特徴空間上での分離超平面を得ることができるようになる!という考えに基づきます.
その特徴空間乗での分離超平面を,元の入力空間へ再度当てはめることによって,非線形の判別関数を得ることができます.
特徴空間上での最適化問題
ここで,サポートベクターマシンの双対問題を特徴空間上に展開して考えてみます.

そうすると,次元拡張によって,φの内積の計算が物凄く膨大の数になることが分かると思います.
特徴空間の次元数 r は,もともとの入力空間の n よりもはるかに大きいのです.
この膨大な計算をどうやって解決するのかがSVMの一つ大きなポイントになります.
カーネル法を用いて,内積計算のコストの削減
カーネル法と呼ばれるテクニックを用いることで,φの内積の計算をものすごく簡単にすることができます.
次のカーネル関数というものを用いて,特徴ベクトルの内積を置き換えます.

カーネル関数を用いることで,二つのφ(x)を直接計算することなく内積を算出できます.
そのため,膨大な計算をしなくても双対問題を解くことが可能です.
つまり,高次元特徴空間への非線形写像を,チューニング可能なパラメータ数を増加させずに得ることができるというメリットがあります.
(双対問題では,特徴量のφ(x)は内積の形でしか存在しない)
実は,このカーネル法を用いるためには,「マーサーの定理」などのある特定の条件を満たさないといけないですが,今回は説明を省略します.
よく使用されるカーネル関数
特徴ベクトルの内積をカーネル関数にて置き換えることが可能ですが,以下の3つがよく使うカーネル関数です.
- 多項式カーネル
- ガウスカーネル
- シグモイドカーネル
それぞれの具体的な関数は以下です.

カーネル関数の魅力
カーネル関数を使用した手法は,学習アルゴリズムと理論がアプリケーションに依存する特性から分離できることが挙げられます.
つまり,アプリケーションとは独立に妥当なカーネル関数を設計すれば良いことになります.
多項式カーネルの例を取り上げる
具体的な例題として,多項式カーネルを使用した計算を行います.
以下のような2次元多項式変換を加えて,2次元の入力空間から,3次元の特徴空間への写像を行います.
(c=0, d=2とした場合のケースを考えます.)
計算してみるとわかりますが,これは,もともとのベクトルx,yの二乗に等しいような関数になります.
φ(x)やφ(y) の内側の計算をしなくても,ものもとのベクトルの内積を素早く計算できます.
これがカーネル法と呼ばれるものです.

SVMに使われるカーネル法のことが分かったかな?



こんにちは。勉強させていただきました。
最後の多項式カーネルの計算ですが、x1x2-y1y2はx1x2+y1y2の間違いでしょうか。