ペルチェ素子を数式モデル化するために大事な基礎

こんにちは．けんゆー（@kenyu0501_)です．

今日は見ておられる方達が，ペルチェ素子を知ってる前提で書きます．
熱電変換素子ですね．
（熱と電気を変換してくれる半導体素子なり！）

ペルチェ素子を初めて知ったB4の時のわいは若干中２病だったので

「この世界のエネルギ形態は変わるぞ！」とか
「産業のイニシアチブは完全に崩れ去る！」とか
「あのハリーポッタの世界が秒でくる！！」とか

原理原則を知らないと魔法とかそんなように思えて勝手に自己震撼していた記憶があります．（またペルチェ素子自体のお話は後で書きます）

さてさて，そんなことはさて置き，今日はペルチェ素子の基本的な原理原則のお話をします．
（修士までの３年間はペルチェ素子とだけ向き合い続けましたのでちょっと憂さ晴らしに詳しく書かせてください笑）

ペルチェ素子の数学的理解をしよう！の前書き

モデル化と一言でいっても，温度を扱うので温度が伝わる方向に次元をとって，0次元とか1次元，2次元など様々ありますが，今回は先ず，
基本的な熱平衡を仮定した0次元1変数のモデル（内側の温度分布を無視して，測定箇所の温度の時間的履歴を追うもの）
をやっていきましょー！変数は一つなので偏微分とかしないから安心して！笑

発電効果の理解

ペルチェ素子は熱電効果によって作用します．
熱電効果とは，熱エネルギーと 電気エネルギーの可逆的変換作用の事ですね！
熱電効果には，ざっと３種類に分けられて，それぞれ

１．トムソン効果
２．ゼーベック効果
３．ペルチェ効果

があります．

トムソン効果

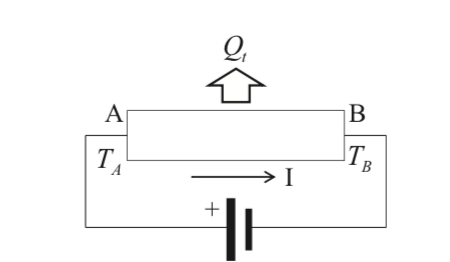
簡単な絵を書きました．
トムソン効果とは，
図のように一つの導体(半導体)中に温度差(TA >TB) が存在する場合，電流 I(A) を流すと，以下の式で表される熱量の発生，吸収が見られる効果になります．
なお注意して欲しいのは，このトムソン効果にはジュール熱は含まれません.

ここで，θ はトムソン係数，I は電流を示しています．
トムソン係数は温度の高い方から，低い方へと電流を流した際に熱が生じる場合に，普通は正となるように定義します.
また，トムソン効果は熱電効果の中でも，影響が限りなく小さい事により，実際の問題では無視する場合が多いです.

（ちょっとリファレンスなくて申し訳ないですが，参考文献を貼って後ほど裏付けしますので待たれよ！）

ゼーベック効果

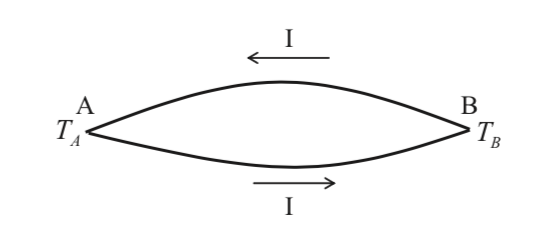
概念的な図を書きました．いちおう，電気的閉回路です笑

ゼーベック効果とは，

図のように二種類の温度差(TA >TB)がある導体または半導体を接続し閉回路を形成した際に，両端に電位差 △V が生じ，回路内に電流 I が流れる効果

です.
この電位差 △V は以下の式で表されます．

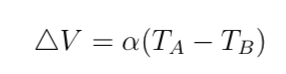
α(V/K) はゼーベック係数です．
接続された導体もしくは半導体により異なりますが，半導体を用いると大きなゼーベック係数が期待できます．
このゼーベック効果による熱起電力によって，熱電発電機の研究が盛んに行われていたりします．

おいらがかつて感動した「この世界のエネルギ形態は変わるぞ！」っていうのは，完全にこのゼーベック効果のせいです．

さらに，半導体材料もしくは金属材料を使った熱電対などの温度測定装置などもこの特性を用いており，高性能なセンサー開発が進んでいたりいなかったりだとか．．.

ペルチェ効果

出ました！ペルチェ効果！！

ペルチェ効果は，

図のように二種類の半導体(N 型と P 型)または金属 A，B を接合したものに電流 I を流すと，電流の方向に応じて接合面では電流 Iの大きさに比例した熱量 Q が吸収または発生し，温度勾配が生じる，

というものです．

この時，熱量 Qp は以下のように書けます.

π(J/A) はペルチェ係数と呼ばれてます．
これまた導体もしくは半導体により異なります.

また面白いことにこれまでの数式を代入して計算すると，ペルチェ係数 π とゼーベック係数 α (V/K) には以下の関係が成り立つことになります．

T (K) は素子の絶対温度です.

ペルチェ効果は古くから知られてましたが，半導体工学の発展とともに効率の良い素子が開発され，各種冷却装置に適用されるようになってますので，もしかすると，20年後とかには，本当にハリポタの正解が到来する可能性があります．

ペルチェ素子のエネルギ収支を数学的に！！

さてさて，基本的なペルチェ素子における効果を整理＆定義したところで，実際にペルチェ素子の放熱面側，吸熱面側の数学的モデリングを施していきます．

図的解釈：百聞は一見にしかず！

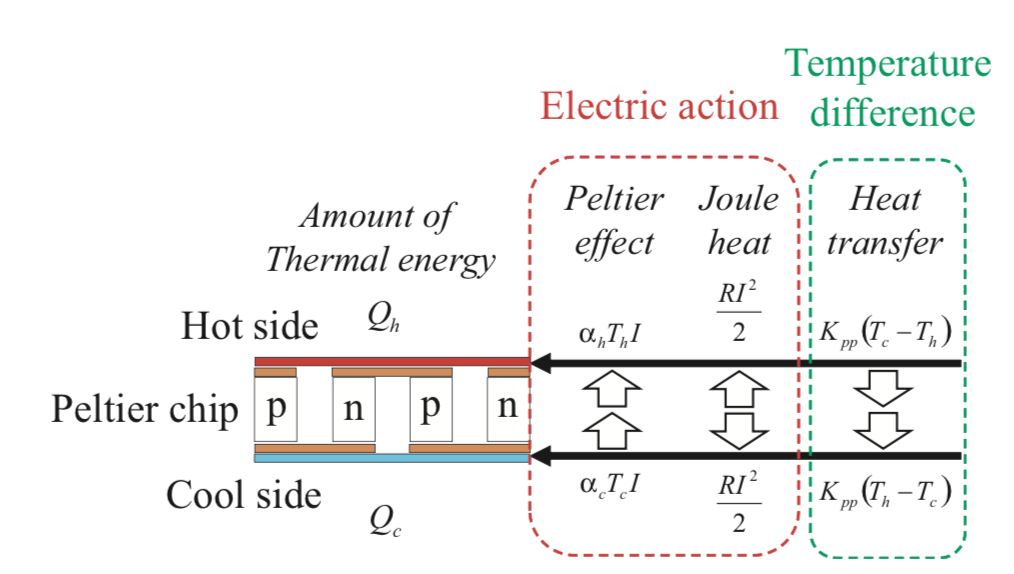
はじめに，ペルチェ素子を水平方向から見た図を持ってきました．
放熱面側（赤）と吸熱面側（青）の熱移動を示しています．

ペルチェ素子に電流をかけると熱移動が起きますが，その時に数学的に取り上げられるモデル化要素は3つです．

1. ペルチェ効果（図の赤い破線）
2. ジュール熱（図の赤い破線）
3. 温度差による自然的な熱移動（図の緑の破線）

の3つです．

また，図に示したようにペルチェ素子の片方の放熱量を Qh とし，他方の吸熱量を Qc とすると，それぞれ以下の式で表される.

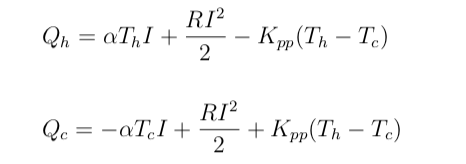
これです！！

おそらく，熱平衡のモデリングを行うとすれば，これが完成形だと考えています．

ちょっと詳しく内側のパラメタや定義をつらつらと書きます．
（ペルチェ素子の熱量を構成する各要素について説明させてください）

Th，Tc(K) はそれぞれ, ペルチェ素子放熱面温度，吸熱面温度を表してます.
各式の第一項は，ペルチェ熱と言って上で書いた熱電効果で導出する事が出来ます．

熱電変換特性を表す指標の一つであるゼーベック係数 α(V/K) は，値が大きいほど，ペルチェ効果によって運ばれる熱量が大きいです（２度目？？笑）.

第二項は，同じく電流によって生じるジュール熱です.
ここでR(Ω) は，ペルチェ素子の内部抵抗値を表します．

放熱面と吸熱面に均等に分配される事が知られています.
電流を流した際に起きる自然的な抵抗分なので致し方ないです．
ちなみにこれは絶対無視してはいけません．

第三項は，温度差が生じた際に，高温側 Th から低温側 Tc に流入する熱伝導を表したものであり，Kpp は，ペルチェ素子内部の熱コンダクタンスです．熱コンダクタンスKppは接触面の伝熱の容易さを表すパラメータです.

即ち，ペルチェ素子の冷却側で吸収される熱量 Qc は，ペルチェ効果による吸 熱量から，ジュール熱の半分と温度差により高温側から流入する熱量を差し引いたもので記述することができます．

よって，熱電冷却を目的とする場合には，冷却性能を維持するためにも，放熱面側温度の熱処理を行わないといけないことが分かります．

また，ペルチェ素子の単位時間当たりの電力 P (W) は，入力される電流 I (A) 及び，電圧 V (V) の関係を用いて，

のように書くことができると思います．
これは単純に電力の式ですね．
更に上で示した Qh と Qc ペルチェ素子の熱流バランスと，電力の式P=EIより，エネルギー収支を考えると，

このように書き換えることができます．

よって，ペルチェ素子に入力される電圧 E(V) は， I で除する事によって，次のようになります．

ここで，上式の第一項は，ゼーベック効果ですね．
ペルチェ素子両面の温度差によって生じる特有の逆起電力になります．

ペルチェ素子の数学的モデリングのまとめ

すなわち，以上をまとめますと，ペルチェ素子のモデリングは，放熱面側と吸熱面側，残りの入力電圧に対して，以下のようになります．

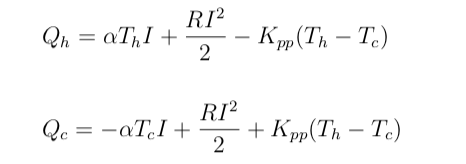
入力電圧は，モデルを動かし，シミュレーションを行う際に重要になるので書いておきました．

はあ，疲れた笑

熱電変換システム設計のための解析―ペルチェ冷却・ゼーベック発電

posted with ヨメレバ

小川 吉彦 森北出版 1998-12

Amazon

Kindle

楽天ブックス