- 二項定理や多項定理をしっかり理解したい人
- 数学が好きな人
- 理系大学生や現役高校生の方
数学をしているとよく出てくる展開式,,,
あれ,乗数がかなり多いと展開がめんどくさいので,必然と二項定理(もしくは多項定理)を使わざるを得ないですよね.

時間のある暇な中学生は,定理を使わないでじゃんじゃん展開をしてくのだぞ!
そこで,今回は,二項定理(多項定理)の定義を確認して,実際に問題を解いて理解を深めましょう!
と言うことで,早速やっていきましょう!
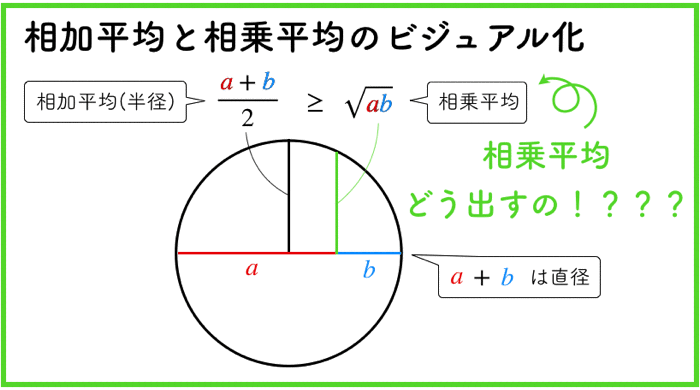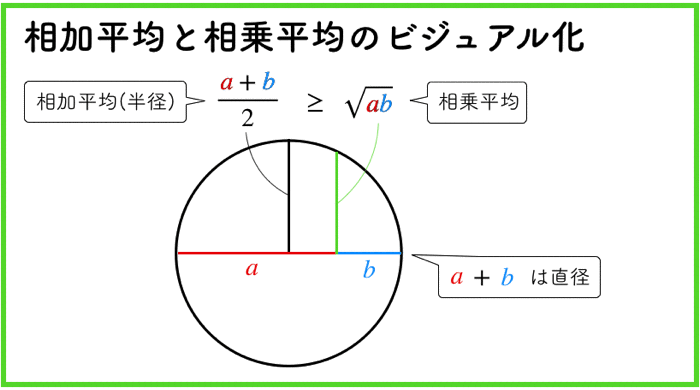
二項定理とは
高校数学だと数2で学習すると思いますが,二項定理とは以下です.
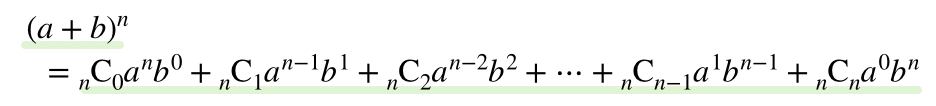
一見複雑そうに見えると思いますが,とても簡単です.
組合せCの式で,各項を展開しているだけで,どのように展開しているかと言うと以下のようになります.


なるほど,結構簡単だな!
つまり,n個の因数(a+b)のうち,r個からbを取り,残りの(n-r)個からaを選ぶ組合せCの積として考えています.
簡単ですよね.
パスカルの三角形
ここで(a+b)のn乗の展開式の各項の係数(二項係数)を具体的に考えて書き出していきます.
(a+b)の5乗まで,考えていくことにしましょう!

二項係数nC0,,,,nCnの値を,nについて上から順に三角形状に並べると,上の図のような三角形ができます.
これをパスカルの三角形といいます.
パスカルの三角形には以下のような性質があります.
- 各行の左右の両端の数は1である
- 左右対象である
- 両端以外の各数は,その左上の数と右上の数の和に等しい

覚えておくと良いことがあるかもしれないぞ
多項定理
これまでは,(a+b)の二つの項だけでしたが,これを3つの項a,b,cに拡張します.
つまり,(a+b+c)のn乗を展開です.
これを多項定理と呼びます.
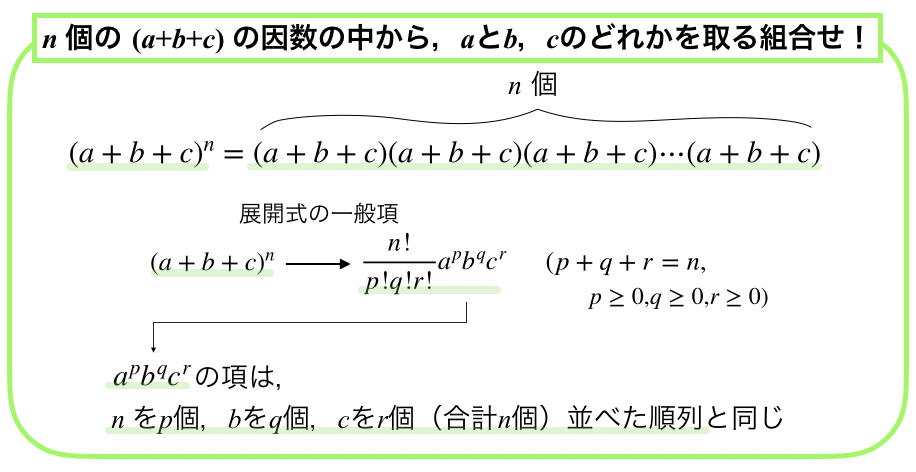
n個の因数a+b+cのそれぞれから,aまたはbまたはcを取り出したn個の文字の積の和です.
この時,項の数は,aをp個,bをq個,cをr個(合計n個)並べた順列と同じ個数だけあります.
多項定理の問題を解く!
数教出版のチャート式(赤)「数学II」を用いて実際に問題を解いていきましょう!
チャート式の問題より
例題2> 次の展開式における,[ ]内に指定された項の係数を求めよ.
(1)(2x-y-3z)^6 [xy^3z^2]
(2)(1+x+x^2)^8 [x^4]練習3> (x+1+1/x)^4 の展開式における定数項を求めよ
赤チャート数学II,10133,p.13
解答
手書きの解答ですが,UPしておきます.



みんなも理解度を深めるために,問題を解いてみてくださいねー!
いろんな大学の入試問題にもよく出るようなので,理解しておくと便利ですー!