打撃加振法によって固有振動数が測定できる理由

こんにちは．
以前，固有振動数と固有モードを計測する実験系のついて記述しました．

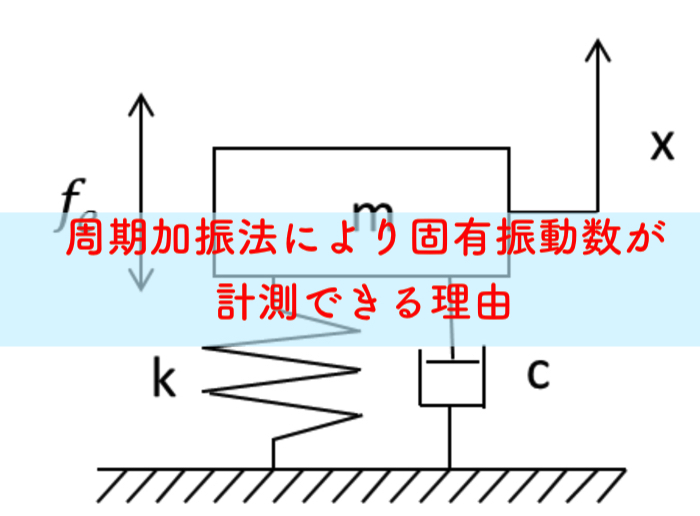
その時は，打撃加振というインパルスハンマーで物体を叩いた時に，固有振動数を測定したのですが，この記事では，なぜその打撃加振法で固有振動数が計測できるのかという理由を考えていきたいです．

議論をするために，1自由度振動系の集中質量系にて，式を考えて，理想的な周波数スペクトルを用いて考察していくことにします．

1自由度振動系のモデル

今回は，片持ち梁を取り上げて，一自由度振動系のモデル化を行います．
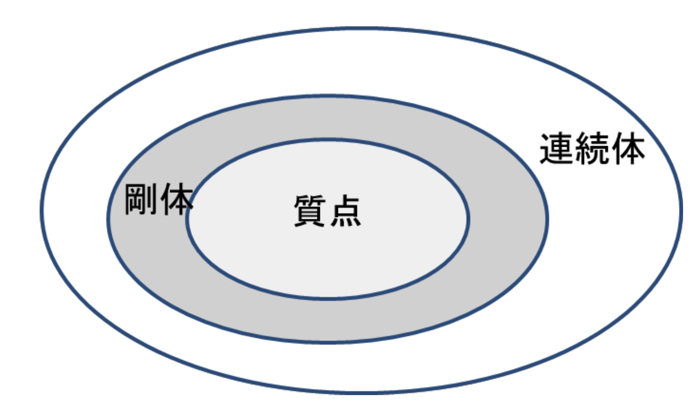
ここで，質点とは？
となっている方は，以下の記事の定義を確認してください．

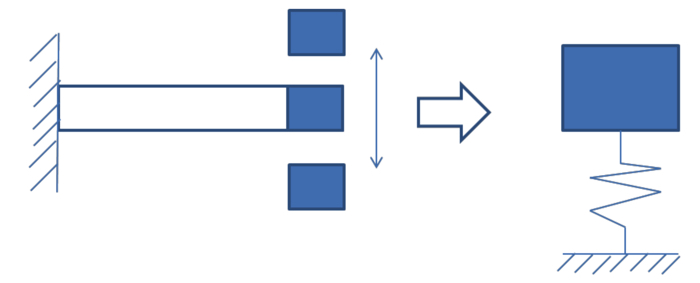
以下が片持ち梁のモデル化です．
梁先端の質量を一つの質点にぎゅっと凝縮して，それが縦方向に振動するというモデリングをしています．

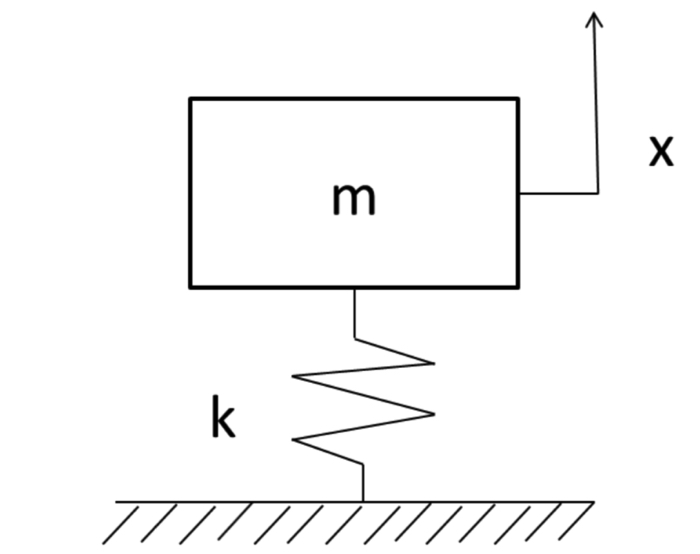
よく振動工学の分野では，考える対象をこのような一自由度のモデリングをすることがよくあります．
このモデルでは，縦方向のみで質量の動きを考えてます．
ちなみに質量の位置に関する変数をxと置いてます．
この質点が振動するための，振動の度合いを表すパラメータとして，バネ定数のkを導入します．

このモデルでは，粘性や空気抵抗は無視しています．

さて，以上のモデルの力の釣り合いを考えて，固有振動数fを導出していきましょう！

固有振動数の導出

以下で，力の釣り合いから考えて，固有振動数を導出していきましょう！

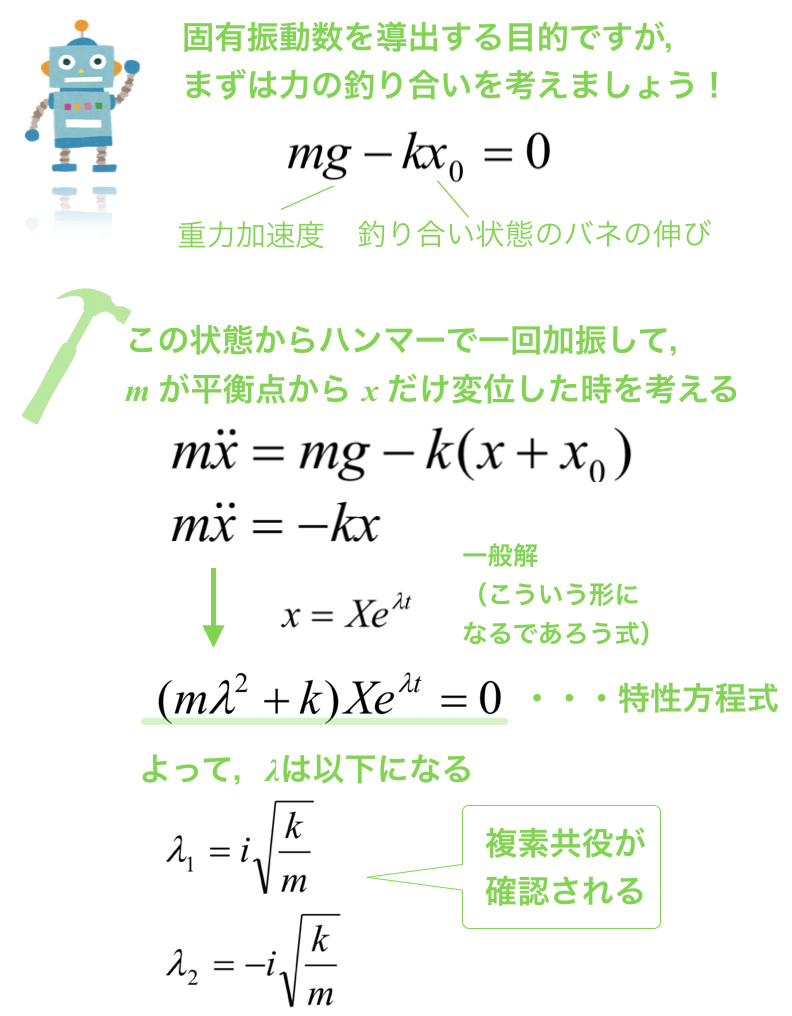
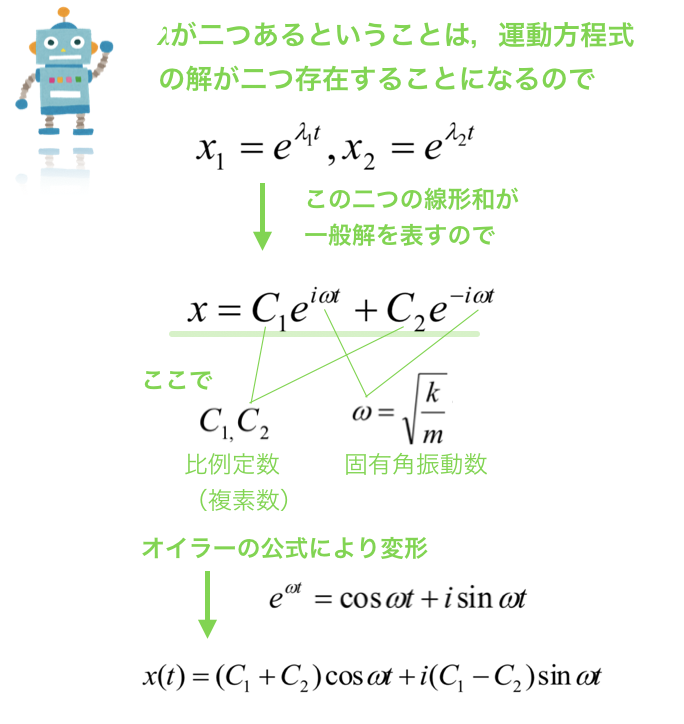
というような感じで，固有振動数を導出することが可能です．
ちなみに，初期位相は，振動の時間的なズレです．
固有「角」振動数は，円運動で考えると，単位時間あたりに進む回転角度を表すために単位は [rad/s] になります．

周波数（振動数）スペクトルはどうなるか？

すなわち，以上でモデル化した一自由度系の理想振動振幅スペクトルは，以下のようになります．

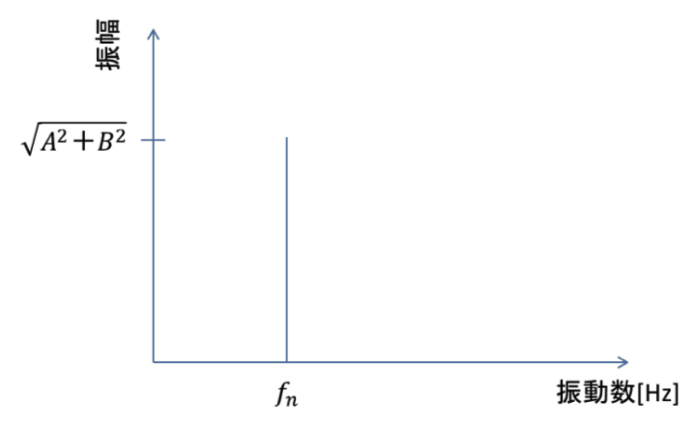
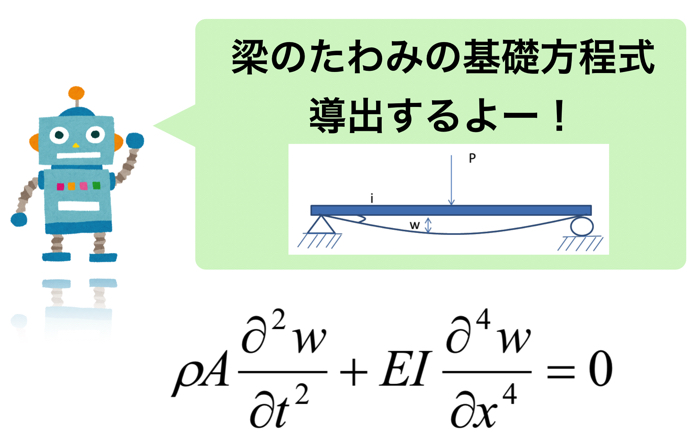
連続体に打撃加振を行うと，固有振動数が無限に存在するので，スペクトル自体は無限に出てきますが，今回は，一つの質点としてモデル化したので，以上のようになります．

これは，先ほど導出した固有振動数と，振動振幅の値によって求めることが可能です．

ではー！