この記事はこんな人にオススメです．
- 1自由度系の振動モデルを勉強している人
- 固有振動数の導出までを理解したい人
- 機械工学を専攻している学生
こんにちは．今回は，粘性を考慮した1自由度系の振動モデルについて書いていきます．
ちなみに粘性を考慮しないモデルについては以下です．
この記事はこんな人にオススメです 機械工学を専攻している大学生 固有振動数について理解を深めたい人 振動や物理…
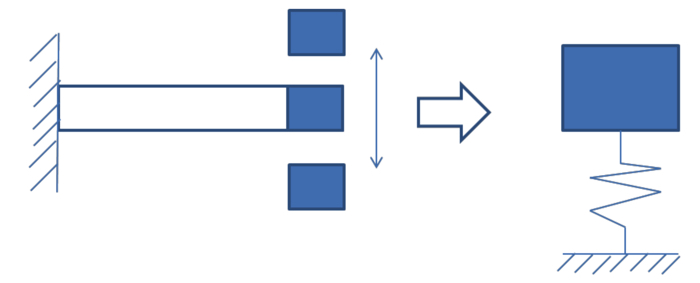
上の記事では，バネ定数のみを考慮して一自由度系の質点モデルを導出してます．
今回は，これに粘性を入れて式を拡張させて，最終的にいろんな固有振動数が出ますが，その時の応答はどのようなものになるのか，（どのようなパラメータに依存して，応答が変わるのか）ということをやっていきましょう！
モデリング
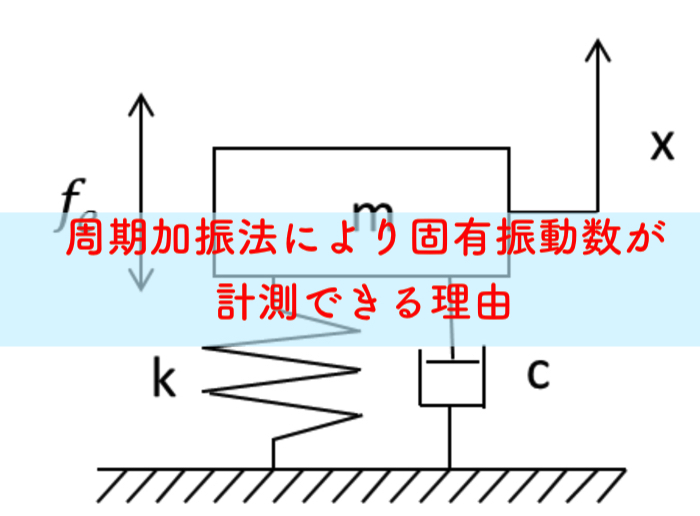
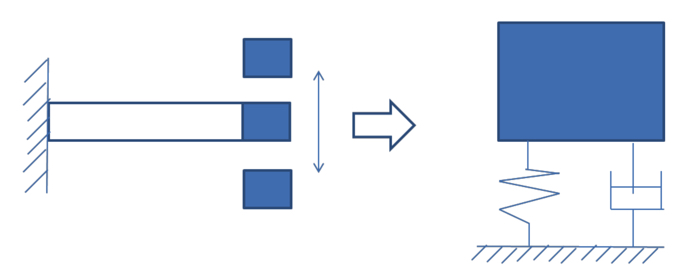
以下に，片持ち梁の粘性減衰力（ダンパーと呼ばれたりもする）を加えた一自由度振動系のモデルを考えます．
粘性減衰力が入ったモデルであれば，空気抵抗を考慮せずとも，振動はいずれ止まります．
前回のバネ定数だけのモデルだけであれば，振動は止まりません．
（もちろん空気抵抗はなし）
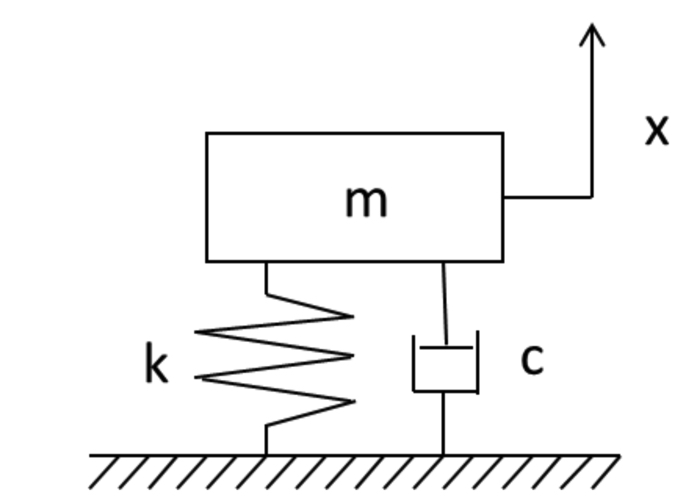
ここで，下のモデル図のパラメータの説明をしていきます．
質量はm，バネ定数をk，減衰係数をcをしてます．
機械工学を学んでいる人なら，すぐに理解できますが，一般的にこのパラメータが使われます．
さて，実際に運動方程式を立てて，系の応答を確認していきましょう！
運動方程式の導出
以下に運動方程式を導出していきます．
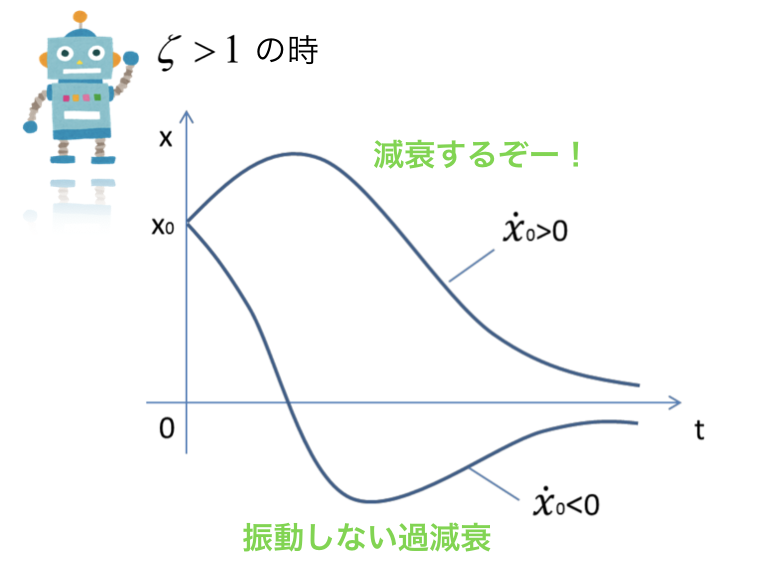
ζ>1の時
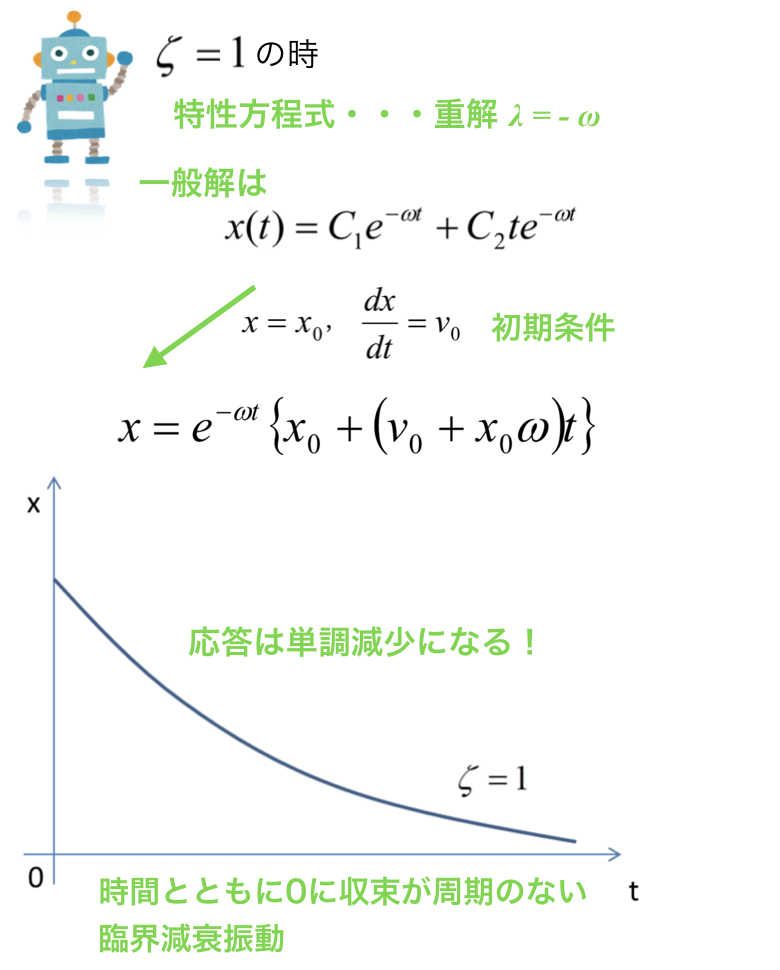
ζ=1の時
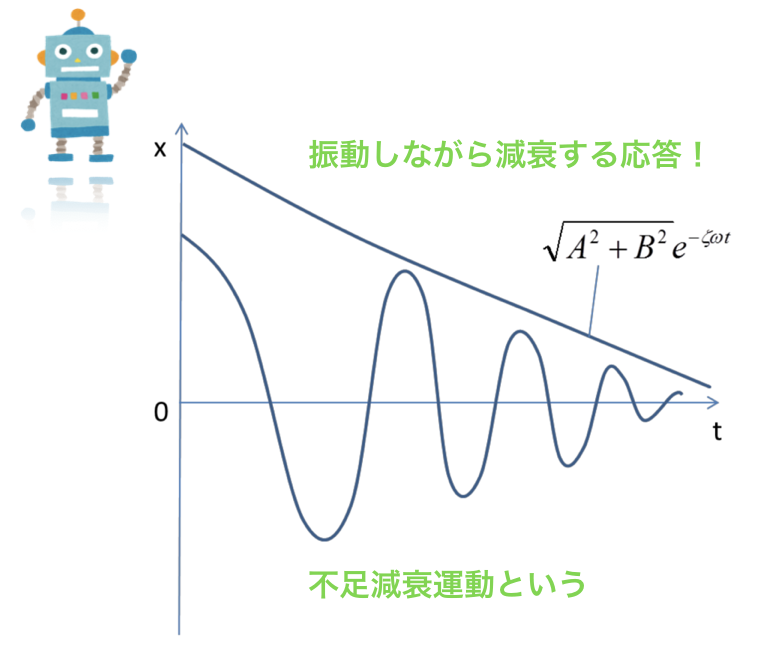
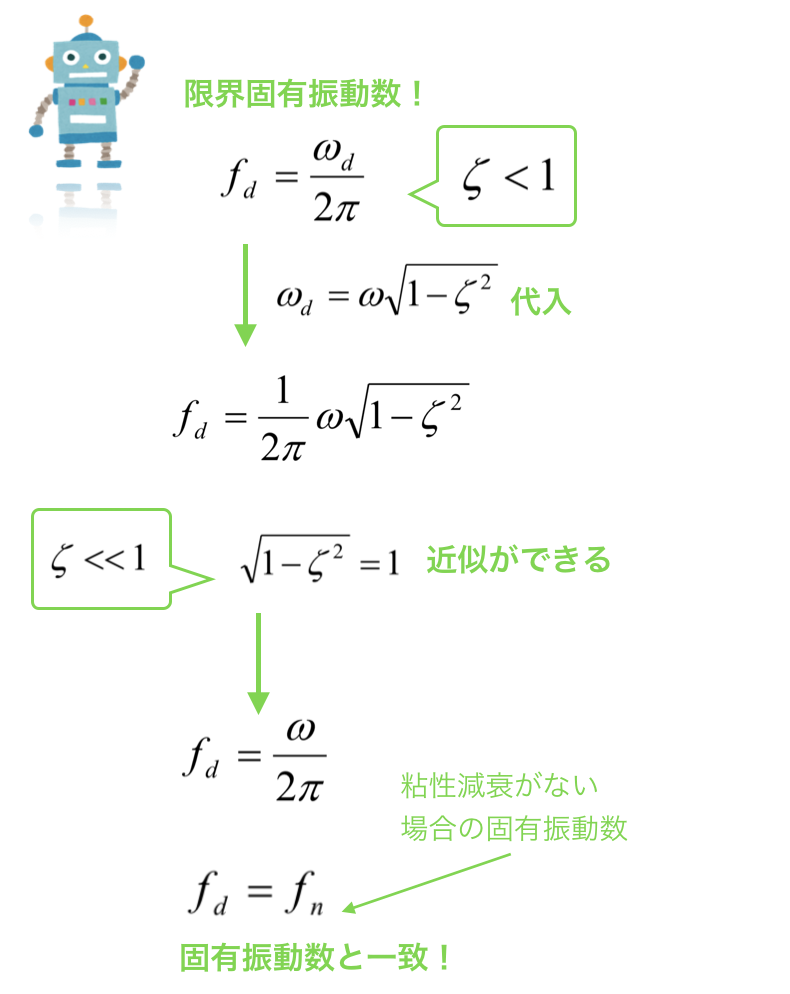
ζ<1の時
最後に
どうでしょうか．
粘性を考慮した1自由度系の振動の3つの応答について理解できましたでしょうか．
機械力学では，これは必ず覚えないといけないところなので，ぜひ身につけてくださいね！
ではー！
こちらの記事もオススメです
この記事はこんな人にオススメです 機械工学を専攻している大学生の人 物理や数学が好きな人 振動に関する分野が好…
