こんにちは.けんゆー(@kenyu0501_)です.
最小二乗法によるパラメータ同定奮闘記も5になりました.
さてさて,現在は何をやっているかというと,「脳波信号から集中状態を判別できるシステム」を作りたい!ということで,数学的モデリングを構築しています.
前回の内容はこちらです.
こんにちは.けんゆーです(@kenyu0501_). 研究アーカイブです. 最近は,毎日研究に加え,スタディサ…
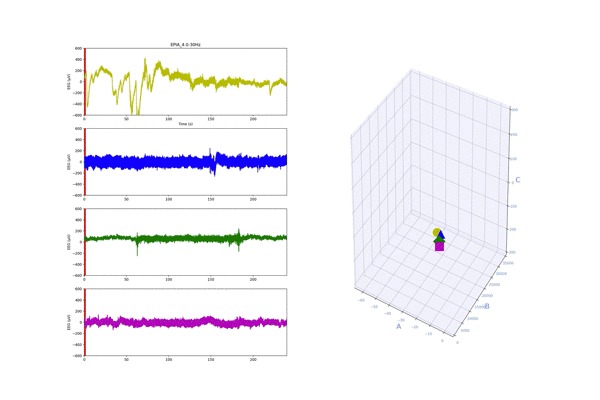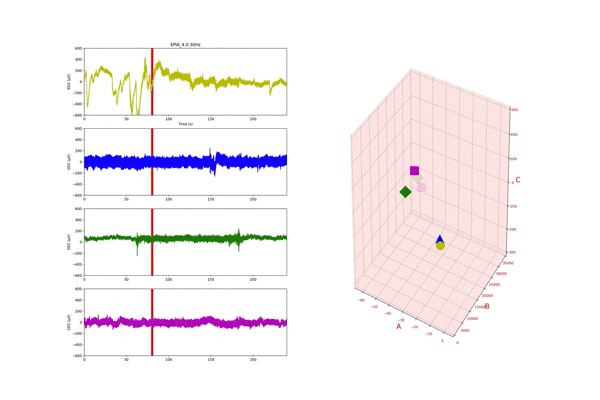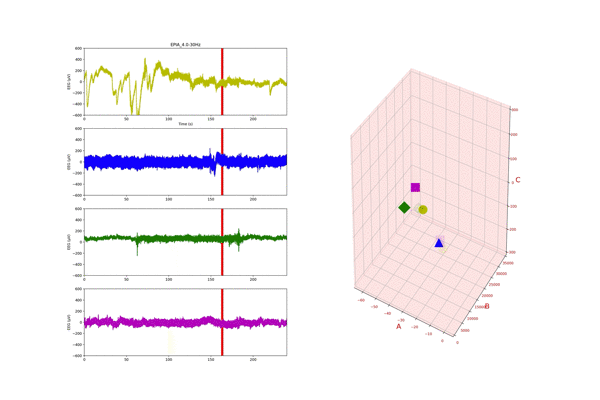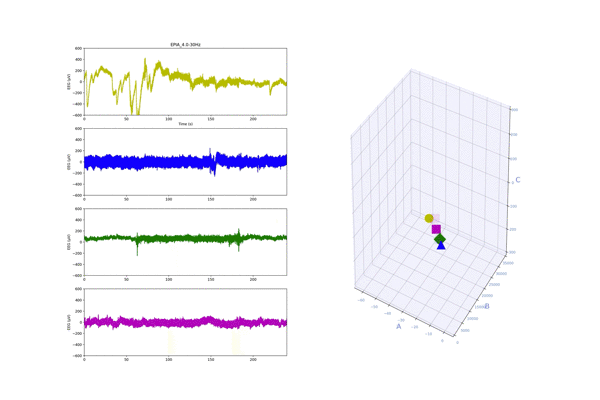
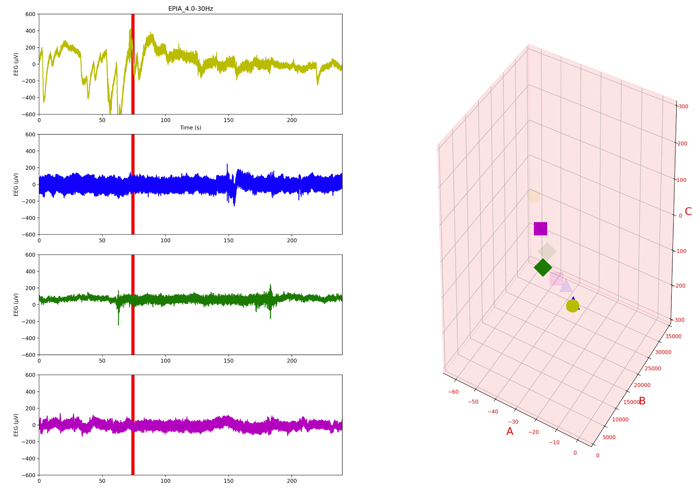
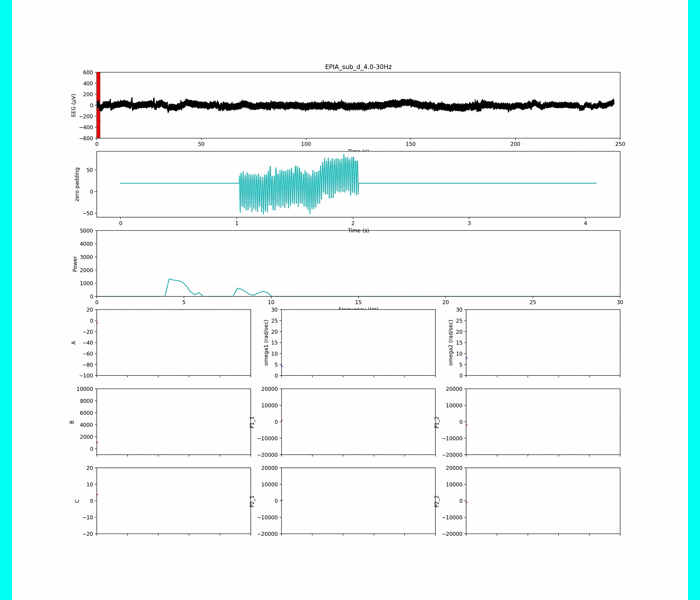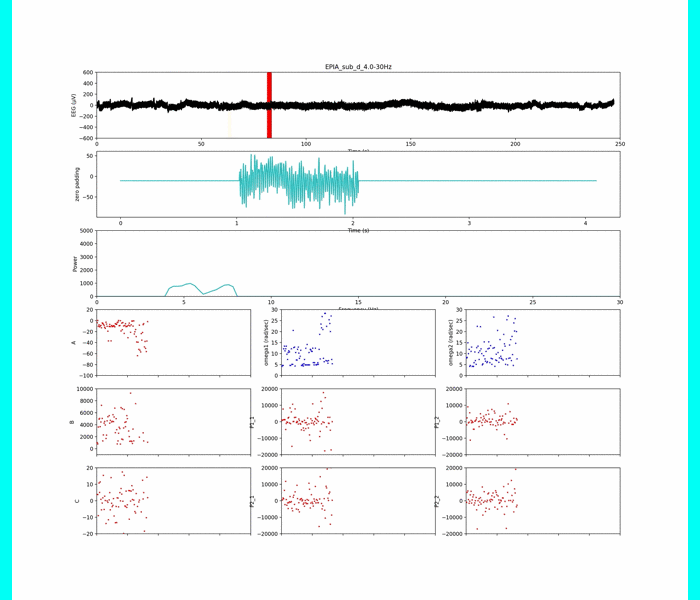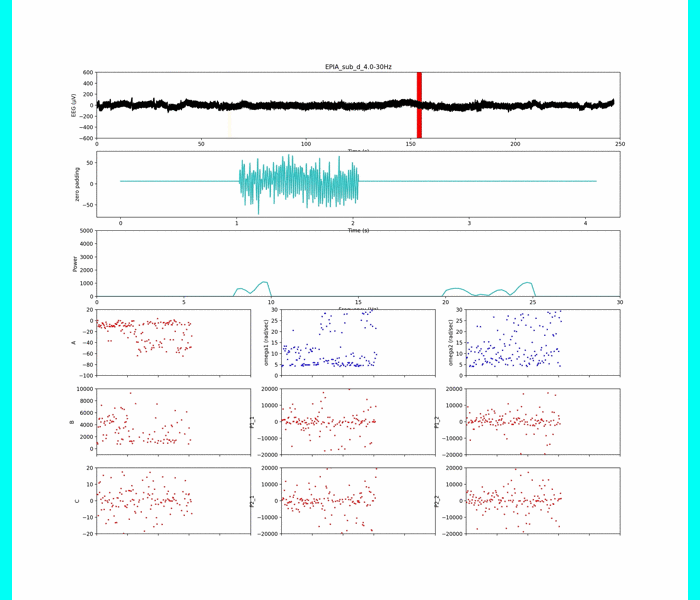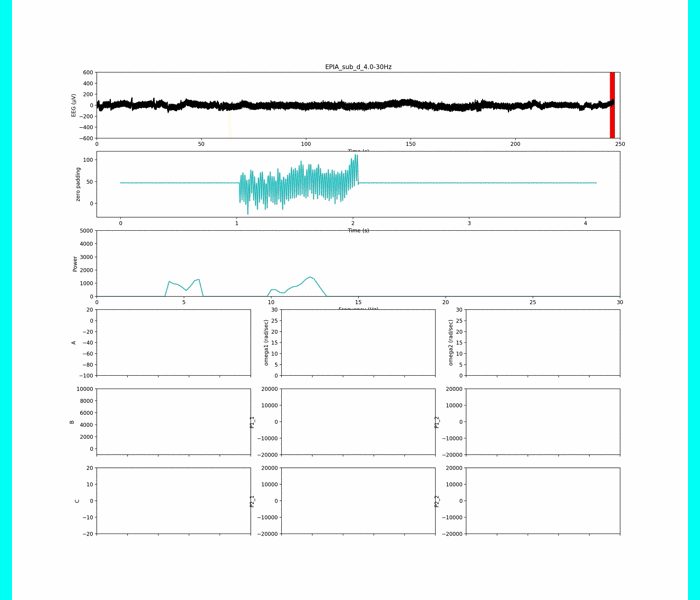
上の動画は,各被験者(n=4)の脳波データの解析をしています.
240秒間脳波の計測をしてて,60秒から180秒は,100ます計算をしてもらい集中状態としました.
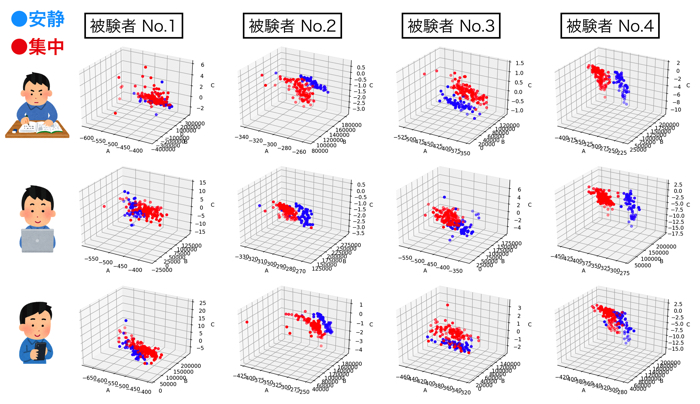
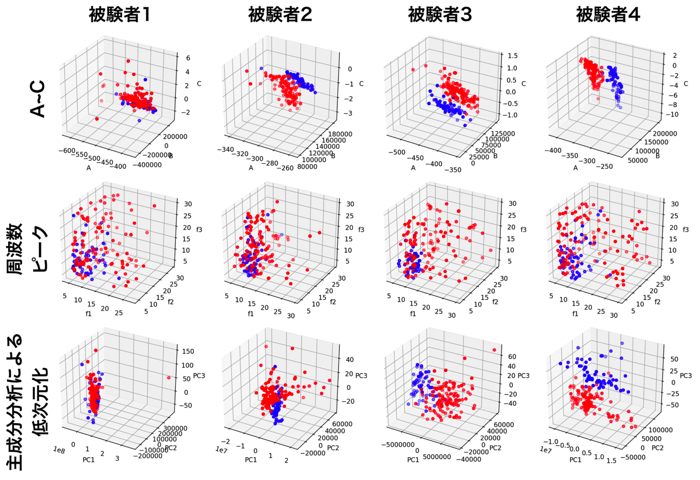
このデータに対して,おいら達の提案手法で解析したものが,右の3Dグラフです.
色の違うプロットが4つありますが,左の時系列の各被験者に対応してます.
60秒から180秒間間の集中状態になると,各プロットが左上に分布するのですよね.
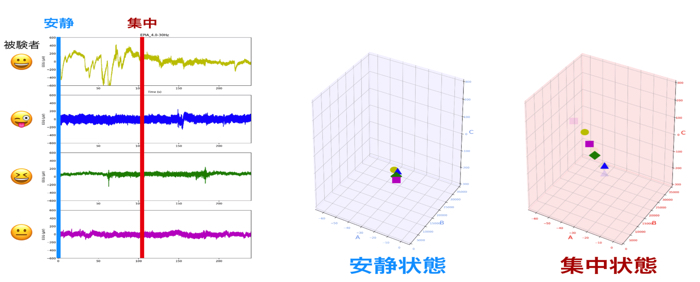
そこで安静状態と集中状態を分ける閾値を,何らかしらのアルゴリズムで線を引きたい!っていうのが現状です.
目で見て分けても良いのですが,,,めんどくさいので(後々なんでそうしたんだ!って突っ込まれるの嫌なので)何らかのアルゴリズムに任せます.
そこで,取っ掛かりとしてサポートベクターマシン(SVM)の導入を図ります.
サポートベクターマシン(SVM)
サポートベクターマシン(SVM)とは一言でいうと,クラスを分ける線(もしくは面)を引くものです.
具体的に知りたい人は,以下をご覧ください.
この記事はこんな人にオススメです サポートベクターマシンSVMについて詳しく知りたい方 機械学習で分類や回帰な…
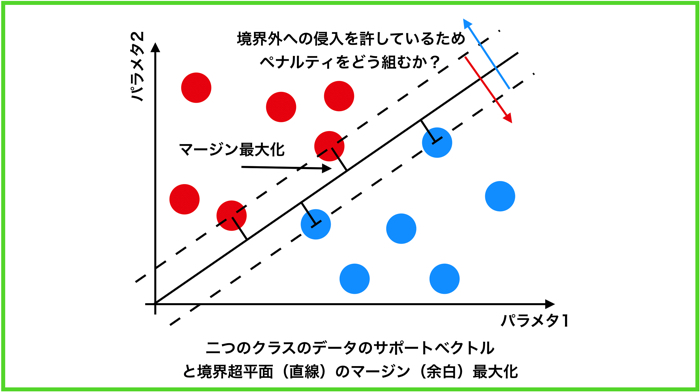
つまり,集中状態と安静状態の特徴量(モデルパラメタ)を持ったベクトル(モデルパラメタ空間に打たれた1つのプロット)を分類するためのアルゴリズムです.
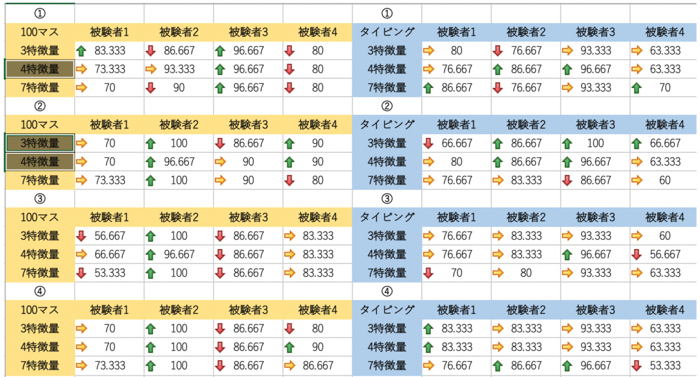
SVMによる分類器を作るにあたって,教師データとテストデータを用意します.
各データの目的は,
・教師データ→分類器を作ること
・テストデータ→その分類器を評価すること
です.
以下のようにしました.
(テストデータが教師データの20%になるように設定してます)
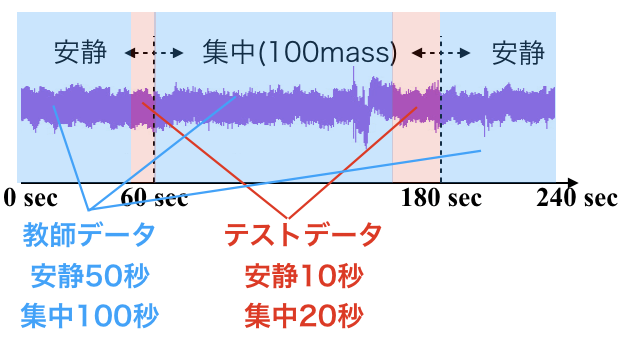
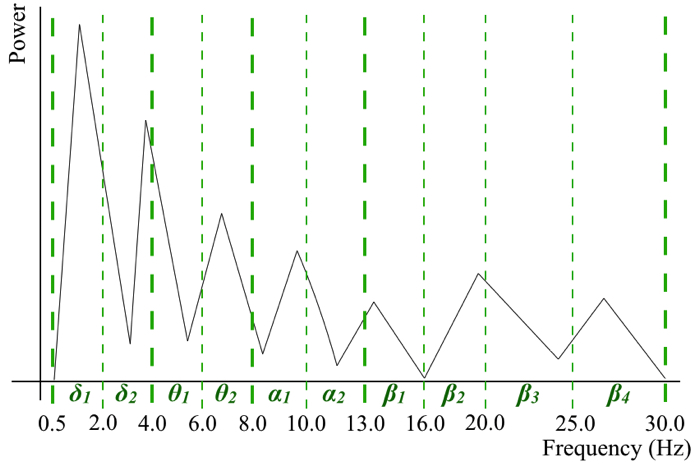
このデータに対して,4-30 Hzに帯域制限した波形を使ってモデルパラメータ同定を行います.
モデルパラメータについては以下の記事を読んでください
2019年になりましたね! 2018年は12月28日に研究納めをしましたが,2019年は1月1日から研究を開始…
これを各被験者ごとのデータに適応させて,SVMで分類ができるのか?(テストデータの正解率をみる)
というのを見ていきます.
分類ができたら,実用に一歩近づきますし,また脳波の特性とモデルパラメタの関連性も考察できると思います.
SVM結果
さてさて,結果は,どうなったかというと...正解率は60%でした.
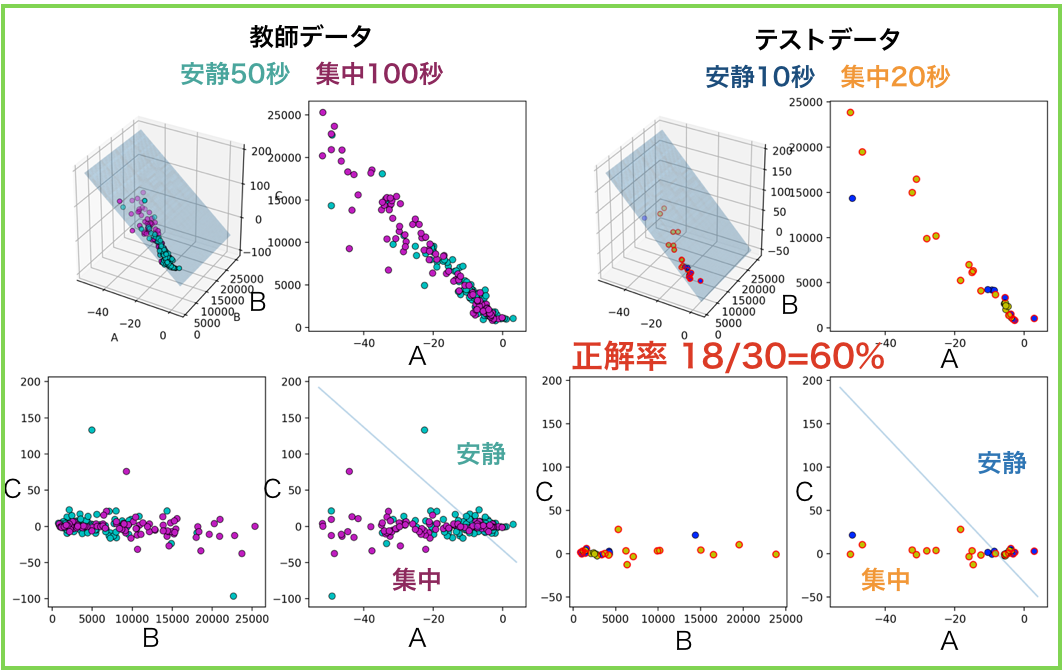
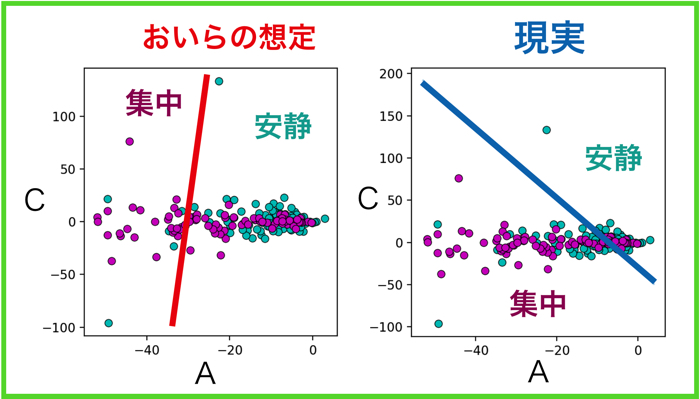
上の図が結果の図です.
SVMのアルゴリズムに任せてモデルパラメタ空間に平面を引いたら,見事に変なところに引かれました.
というよりは,なんかおいらの想定と違う...
(以下が頭の中で描いていた想定のSVM線です)

おいらの想定だと,結構きれいな平面が引けているのですが,実際今回組んだSVMのアルゴリズムだと上手く機能してくれませんでした...
とほほ
状態としては,集中か安静かの2択(50%)なので,現状の60%ではまだまだ正解率として低いと感じます.
これを95%くらいまで持っていきたい...
問題点とこれからの改善点
以下のことが問題かな,と思っていたりします.
- 分離可能(集中と安静の状態)なデータを前提として扱っていたが,コンピュータ的にはそうではない.
- 二つの状態を示す各ベクトルが入り混ざってるものがある
- つまり特徴量の設計が甘い
- 境界外への侵入を許しているため,ペナルティを組み込まないといけない
- そもそもSVMじゃ限界があるのか.
- ニューラルネットワークNNを実装するか
などなど,色々と手を伸ばしていきます.
NNはまだもう少し先の話ですが,最終的にはそこに行き着きそうです.
まずはSVMの設計をします.
研究の経緯の話
昨年は,脳波信号の特性を説明するために,モデルパラメータを調べていました.
脳波の挙動を模擬するようなモデルパラメータの同定は大変で,遺伝的アルゴリズムGAを使ってました.
1年くらい時間はかかりましたが,提案する非線形な数学的モデルが,脳波の挙動を示すモデルである事を唱えました.
今年は第2フェーズです.
脳波の特性をある程度説明するモデルということが分かったため,それを使って実用したい!というのが今年です.
GAによるパラメータ同定は,環境(目的関数)に合うように多くの世代を経由してパラメータが決まるのでかなり時間がかかります.
リアルタイムでパラメータを同定していくには,もっと高速に逆問題を解く手法が必要なので,現在は最小二乗法という方法を使っています.
(モデルパラメータの変数の分だけ偏微分が0になる関数を解くだけで定まるので計算が速い!)
まだまだ先は長いですが,いろんな手法を片っ端から試して,プログラムを組んで,自己研鑽していきます.
SVMのプログラムの公開
以下のページで,SVMの解説とプログラムの公開を行っています.
この記事はこんな人にオススメです サポートベクターマシンSVMについて詳しく知りたい方 機械学習で分類や回帰な…
ではー!