2重振り子でカオスの特徴について触れておく

こんにちは．けんゆーです（@kenyu0501_)
ということで，今日は2重振り子について勉強するついでに，カオスの特徴について少し書きます．
機械工学を専攻する学生であれば，一度は2重振り子について学ぶと思います．
しかし，それが示すカオス性まではなかなか学ぶことも少ないと思いますので，見ていただければ嬉しいです．

カオスの特徴である初期値鋭敏性

2重振り子を観察していると見られるのが，初期値鋭敏性．
これはどんな性質かというと，初期値（振り子が運動をスタートさせる初期位置や初期速度）が少しでも変われば，その後の変動はとても大きく変わるということです．
以前に，ダフィング振動子で試しましたが，初期値がほんの少しでも変化すると，t→∞で挙動は全くの無相関になることでした，
（参考「ダフィング振動子とファンデルポール振動子の時系列アニメーション」）

さてさて，今回はそんな面白いカオス性という性質が簡単にシミュレーションできる系として２重振り子を題材にします．

２重振り子について

系について

２重振り子は以下のような系です

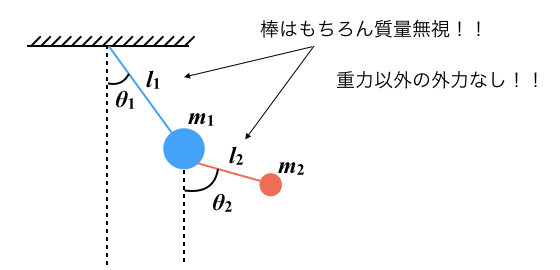
θ1とθ2に関する運動方程式が記述できれば，シミュレーションが可能なので運動エネルギとポテンシャルエネルギ，さらにラグランジュ関数より導きます．
（参考書：力学系カオス，森北出版，p.133）

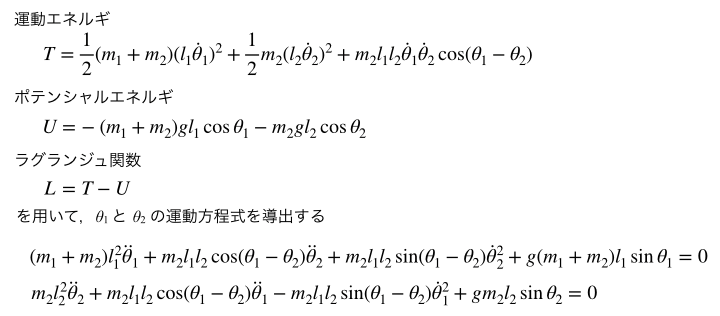
パラメータ，初期値，狙い

参考図書の力学系カオスより，おもりm1，m2や，棒l1,l2のパラメータの値を参考にしました．

• m1 = 10
• m2 = 1
• l1 = 2
• l2 = 1

初期位置θ1とθ2に関しては，

• θ1 = π/2
• θ2 = π/2

θに対する初期速度dθ1，dθ2に関しては．

• dθ1 = 0
• dθ2 = 0と0.1
  ※おもり2の初期速度だけ2つのパターン試して，カオス的挙動を確認します．※当初は2つを考えていましたが，今は一つのみ！(dθ2=0のみ)
  

パラメータに関して，m1 > m2，l1>l2 としたのは，カオス的な変動を確認するためです．
おもり1は2に比べてかなり重いので，周期的運動に近い動きをしますが，おもり2はすごく活発で激しいカオス的な運動をします．

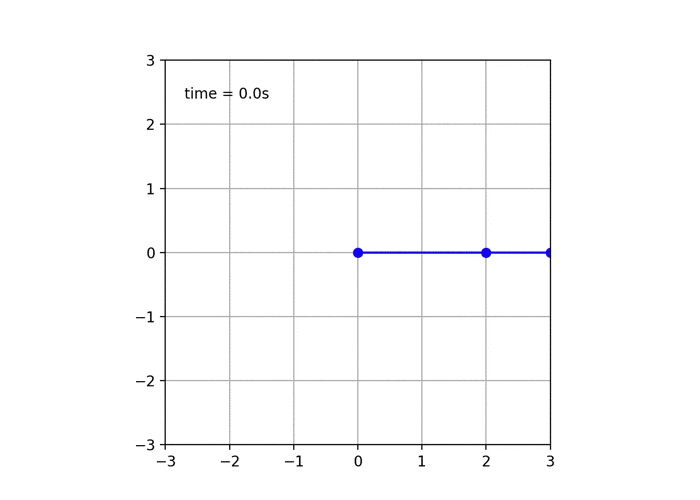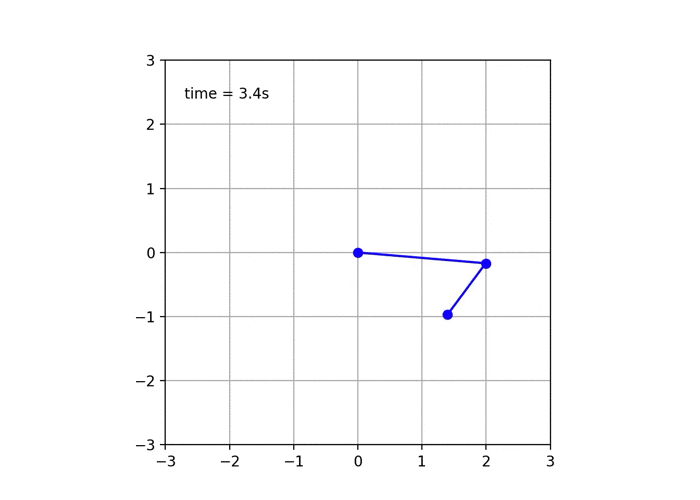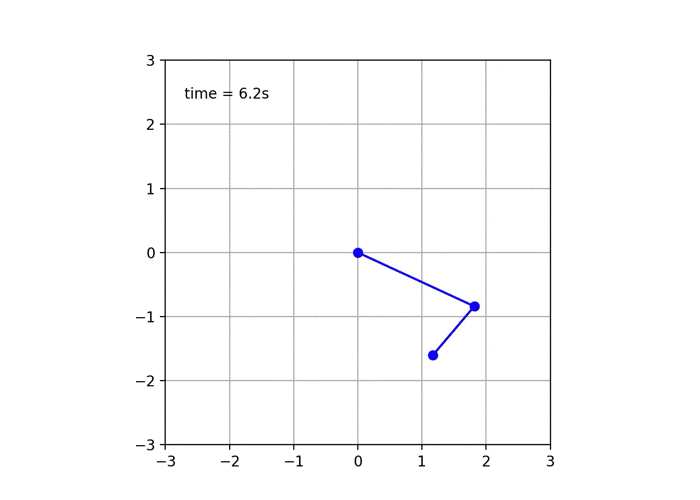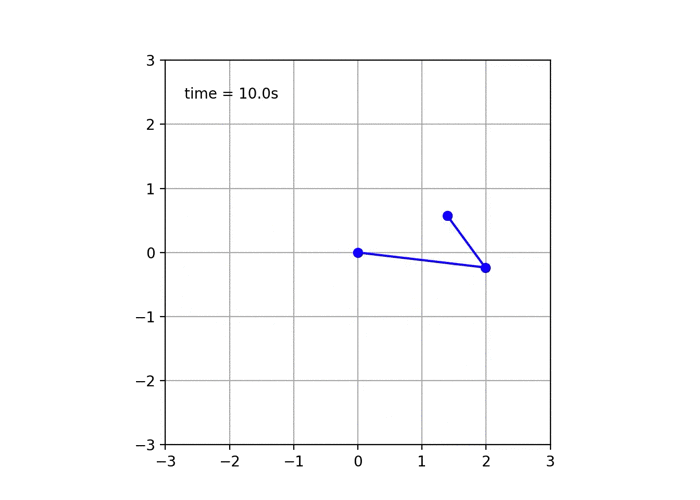
カオス的挙動の確認

dθ2=0 (m/s)

グラフが見辛くてごめんね！