- チェバの定理・メネラウスの定理をかなり分かりやすく解説!
- 頂点→分点→頂点→分点→頂点→分点!
- チェバは点,メネラウスは線,別に三角形と交わらなくても良い!
こんにちは.けんゆー(@kenyu0501_)です.
2020年のセンター試験 数学1Aの試験でも出題された「チェバの定理・メネラウスの定理」の絶対に忘れない覚え方を共有したいと思います.

一筆書きをするのは分かるけど,どこを通るのか分からない!!!
一筆書きの要領で,公式を暗記したと思いますが,大事なのは全て,
頂点→分点→頂点→分点→頂点→分点
に従うだけ!ということです.これを意識しておくだけで,試験ではパッと解くことができます.
早速,それぞれの定理を見ていきましょう!
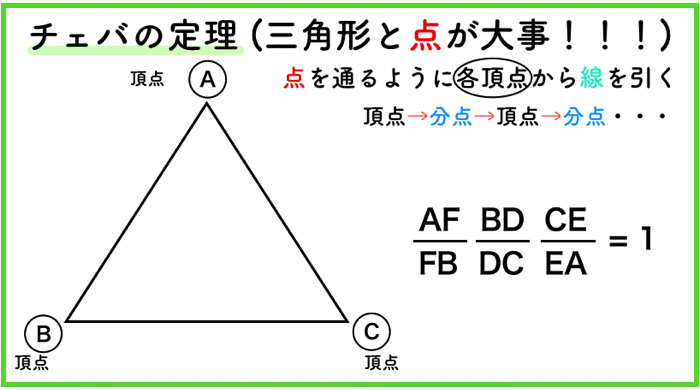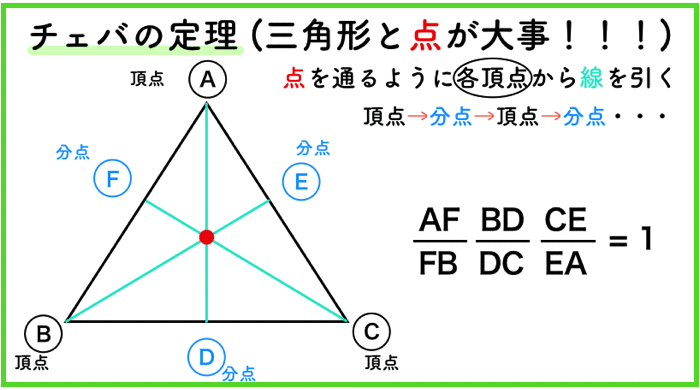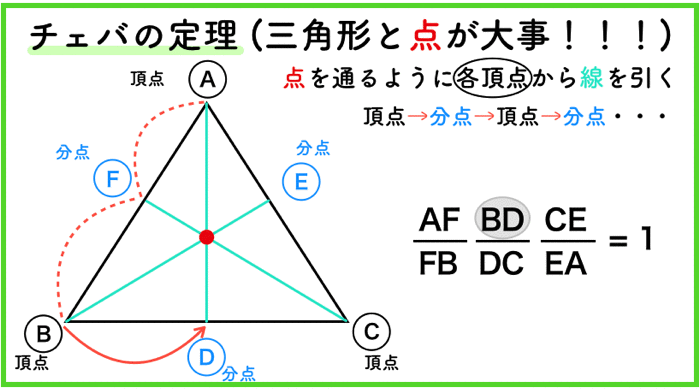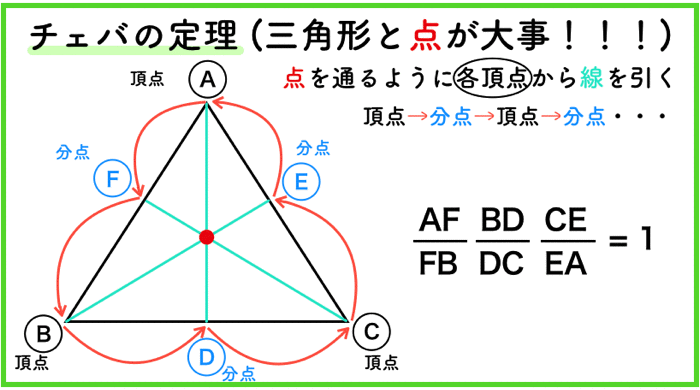
チェバの定理

チェバの定理は「三角形と点」の関係のみが大事です.
三角形の頂点と点を通る直線を引くと,三角形のもう一辺に交わります.
これは内分点になります.
これを分点と呼びます.外分点の場合もあるからです.
さて,分点を3点出せたら,後はおなじみの,
頂点→分点→頂点→分点→頂点→分点
に従うだけです.

記号は特に意味がないよ!頂点と分点を交互に行き来するということが大事!そしてスタートはどこからでも良いよ!
点は三角形の外にあっても良い!
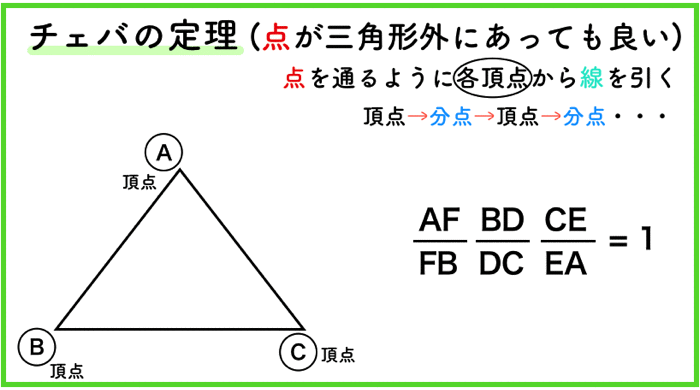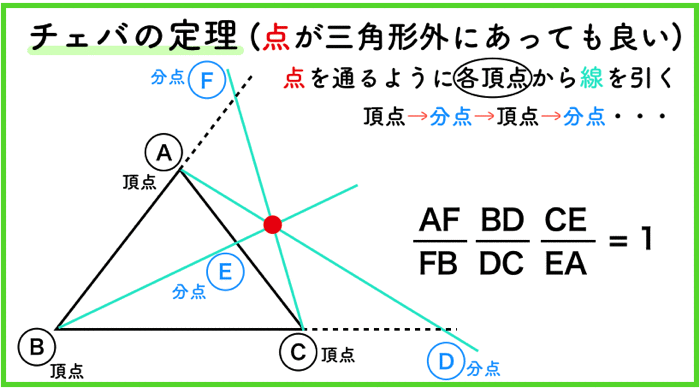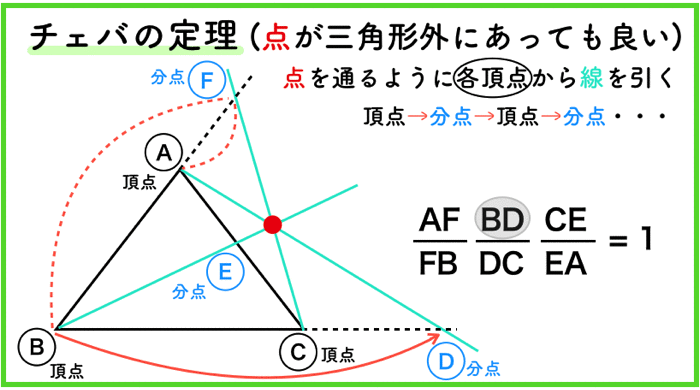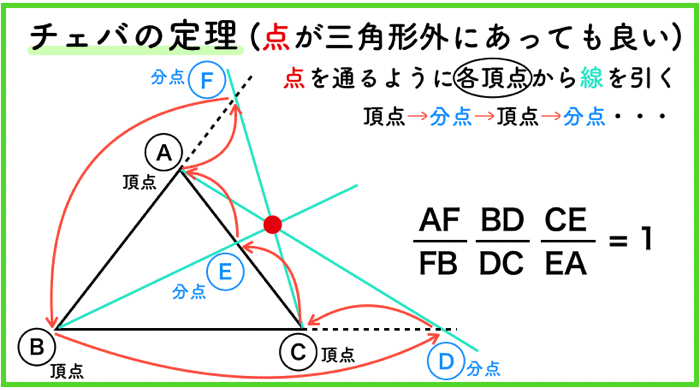
頂点→分点→頂点→分点→頂点→分点
のルールさえ守れば,点の位置が,三角形の外部にあったとしても,あの公式は成り立ちます!!!
メネラウスの定理
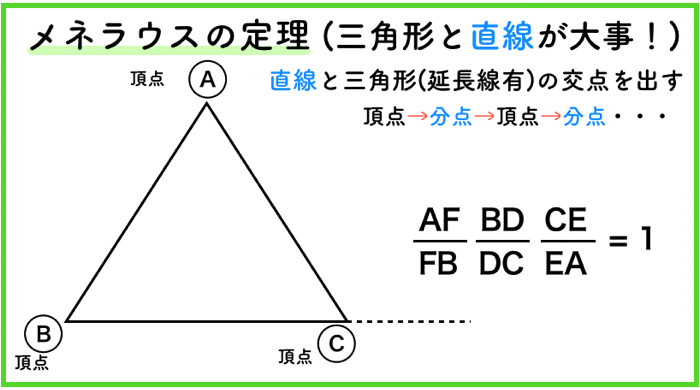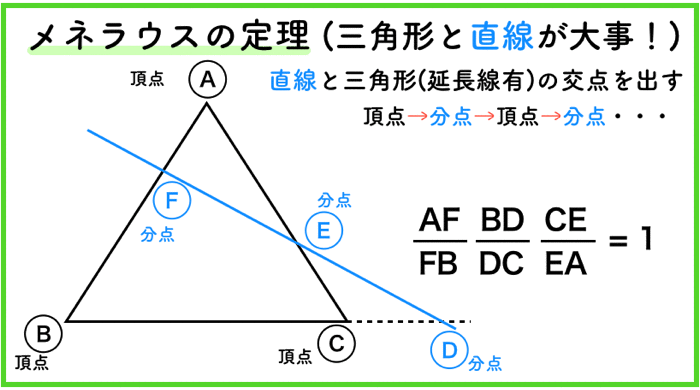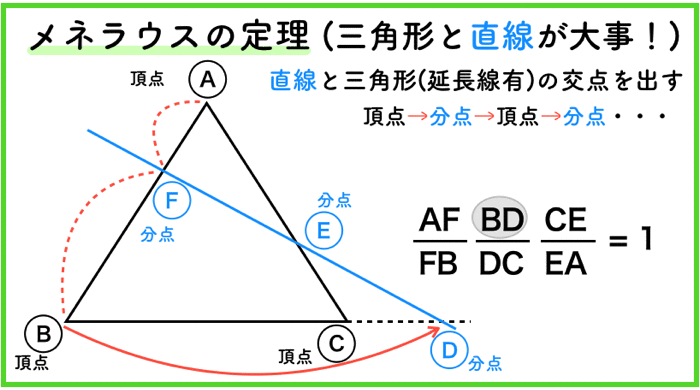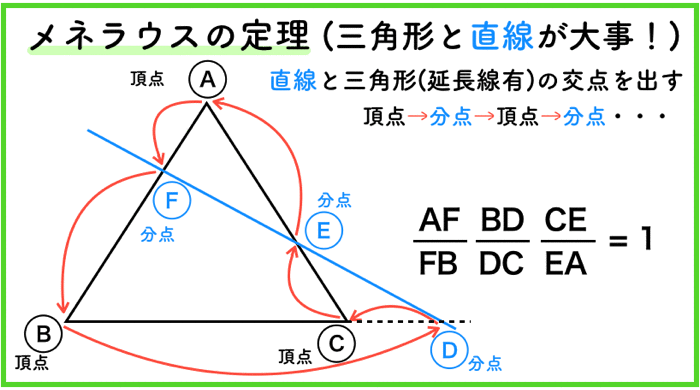
メネラウスの定理は,「直線と三角形」が大事です.
チェバは点でしたが,こっちは線です.
交わる交点,もしくは三角形の延長戦との交点は,内分点もしくは外分点になっているはずです.
これを分点とします.
そうすると,後は,
頂点→分点→頂点→分点→頂点→分点
に従うだけです.簡単ですよね.

何度も言うけど,記号は全然,意味がないよ!頂点と分点を交互に通るということが大事なんだね!
直線は交わらなくても良い
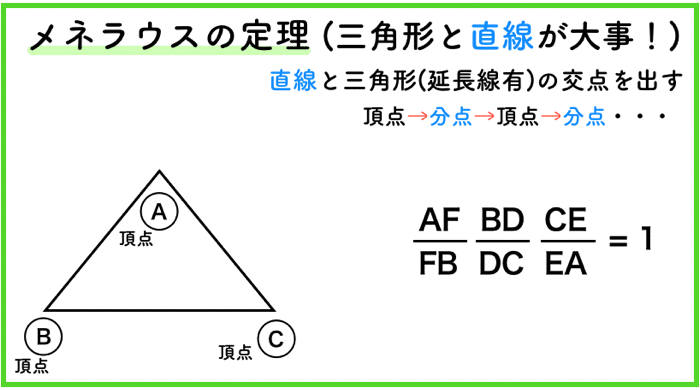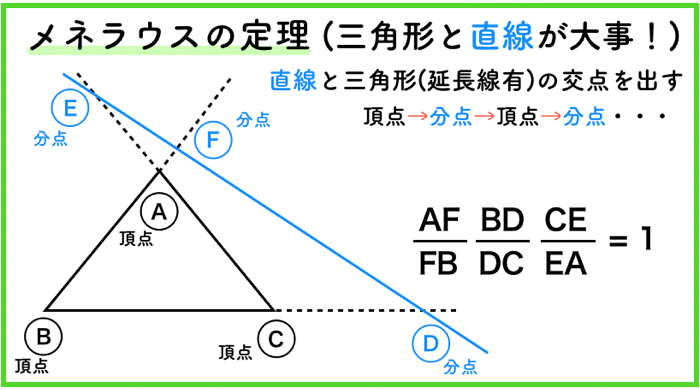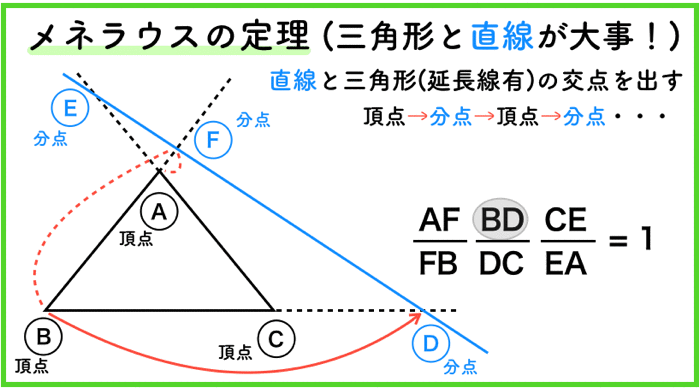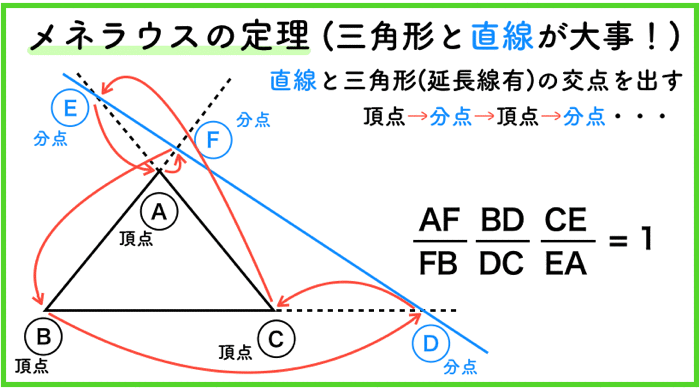
ここまでくると,もうお分かりかと思いますが,メネラウスの定理は,別に直線が三角形と交わっていなくても成り立ちます.
延長戦との交わりが外分点になるためです.
後はもう,簡単ですね!

スタートの位置はどこからでも構わないよ!
こちらの記事もオススメです!