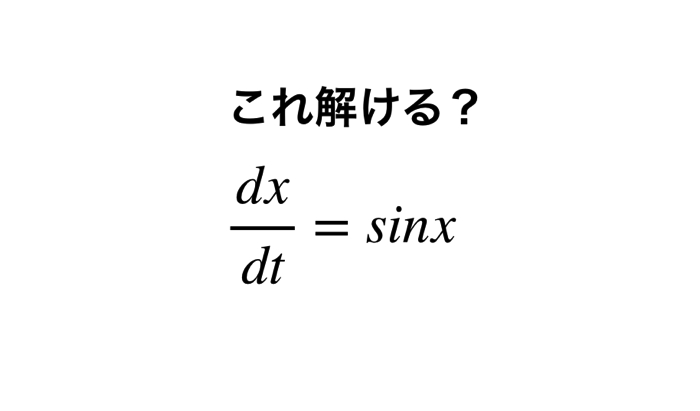
- 非線形系の解析に興味がある人
- 数学が好きな人
- ストロガッツの非線形ダイナミクスとカオスが気になる人
こんにちは.今日は非線形についての記事を書きます.
いきなりですが,こちらの式(dx/dt = sin x)は非線形な微分方程式でしょうか?
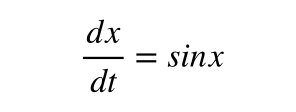
数式上,こちらは紛れもない非線形方程式です.
今日はこの,dx/dt = sinx の解を図的解釈で求めていきたいのです.
ん?そもそもこれがなんで非線形なの?
と言う疑問もあると思うので,そういった数学的定義の後に,解を考えていきましょう!
また,解き方のプロセスをより詳しく知りたい人はこちらの本がオススメです.
(ストロガッツ 非線形ダイナミクスとカオス,田中久陽,中尾裕也,千葉逸人,丸善出版)
線形系と非線形?
常微分方程式に話を限定させてください.
常微分方程式というものは,一般的にこのように書けるわけです.
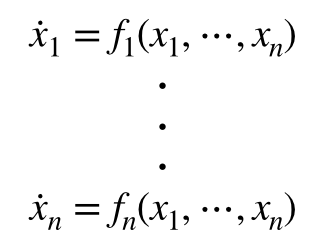
xの上についている点(・)は,tについての微分です.
関数fの中にある各変数xに関しては,なんでもいいのです.
ある物体の速度でも変位でも良いですし,ある生物の個体数でも良いかもしれません.
さてさて,ここまでは常微分方程式の形です.
では,例えば,機械振動系で有名な線形の粘性減衰振動系を考えます.
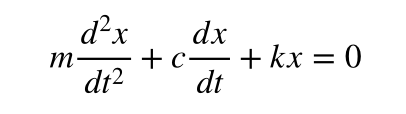
これですね.
こいつは線形の微分方程式です.
ちょっと以下のスライドのように式をいじくり,線形系を示します.
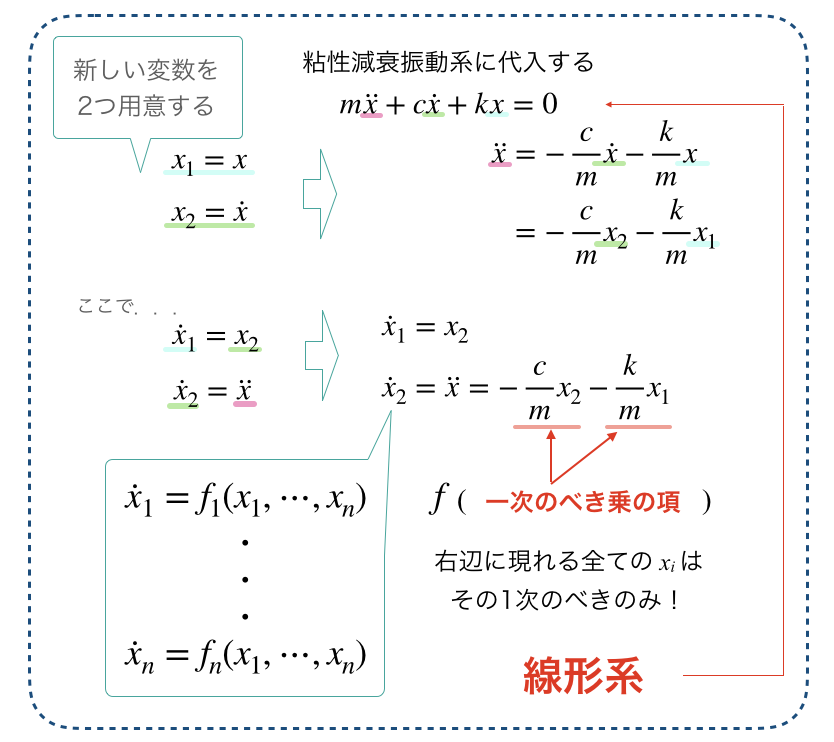
どうでしょうか.
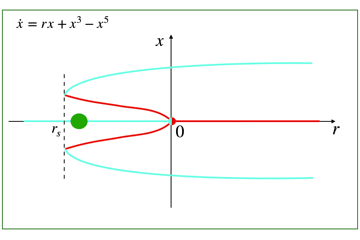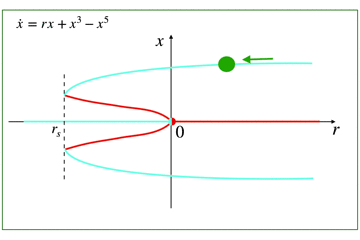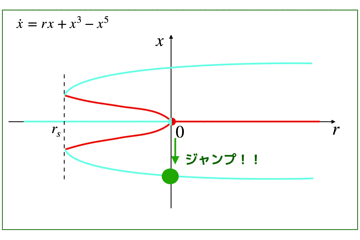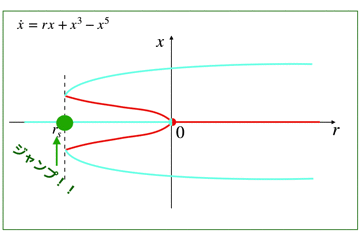
状態方程式でその系を記述した際に,一次の項とそれ以外で定義づけるのが,線形と非線形です.
つまり,右辺のfの中身が,一次の項(線形)のみでなければ,非線形と呼びます.
代表的なものは,xの3乗だったり,xの積であったり,関数形(sin x) だったりします.
非線形微分方程式の解を求める!
これ
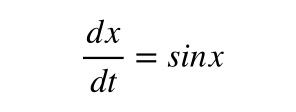
解けますでしょうか.
閉じた系ですごく簡単と思うかもしれませんが,以下で考えてみましょう.
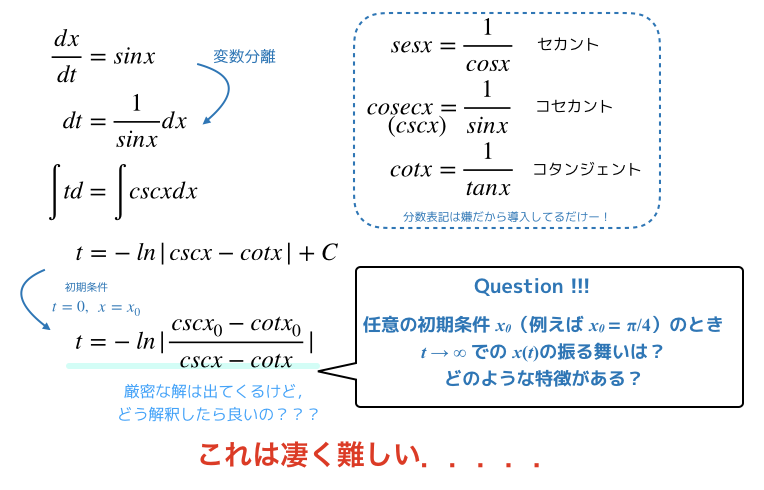
結構簡単だと思われたかもしれません,
非線形な微分方程式,なめちゃいけません.
実はこれ正攻法で行くとかなり難しいのです.
では,どのようにやるか?
図的理解で簡単な非線形微分方程式を解きましょう!
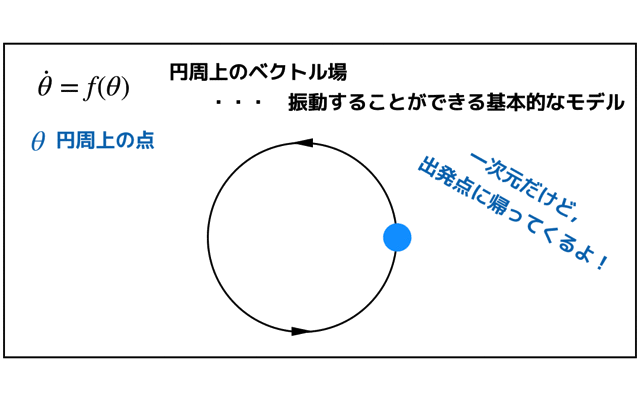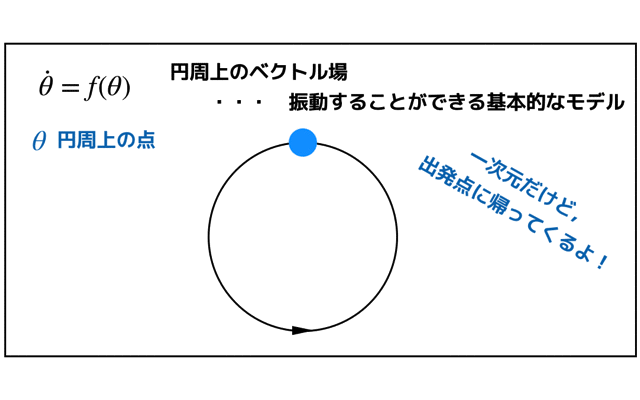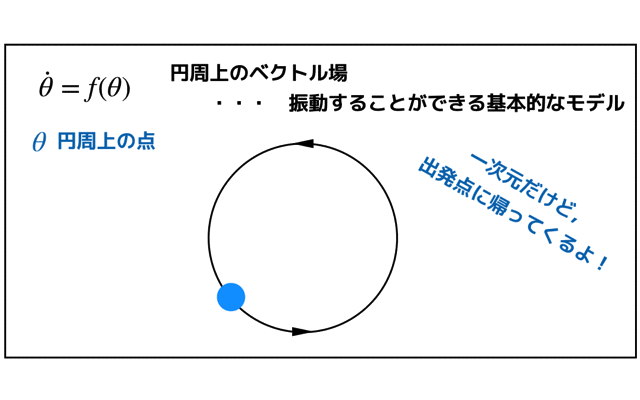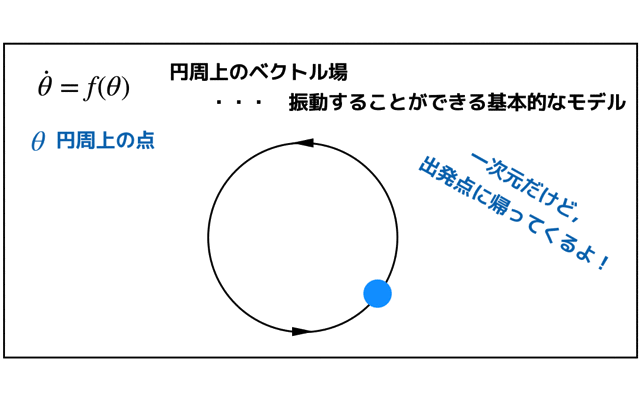
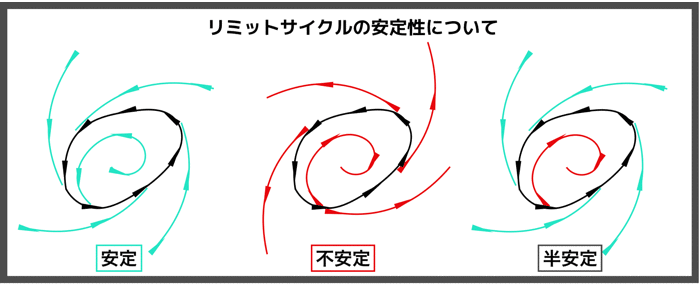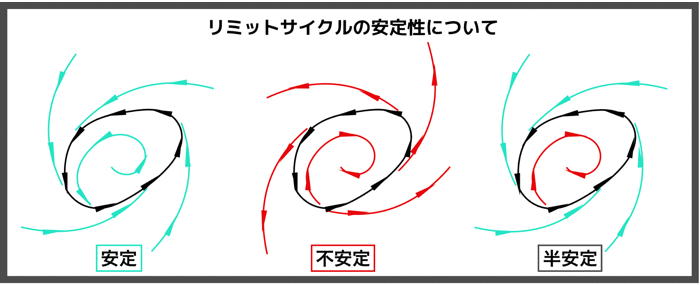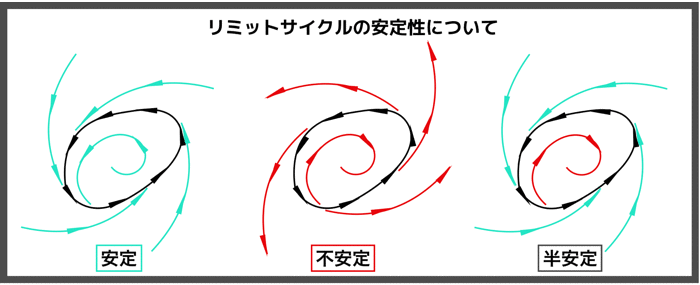
ベクトル場を用いることによる図的解釈で簡単に解が求まります.
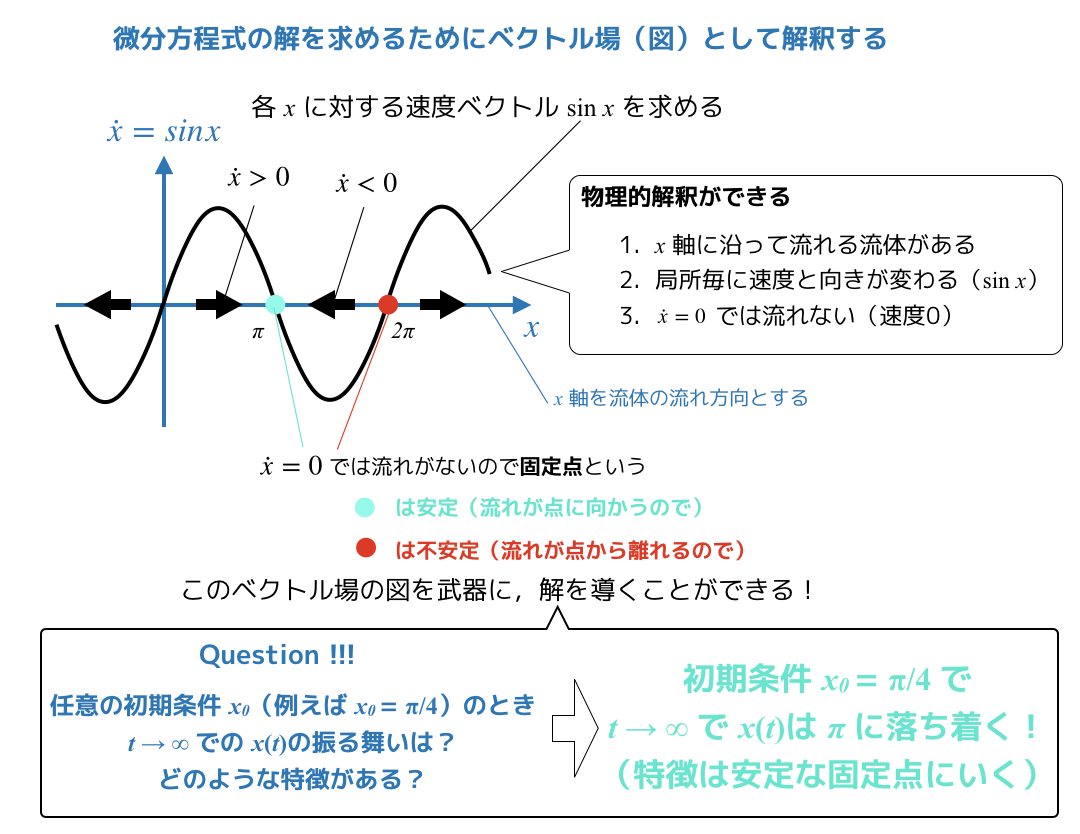
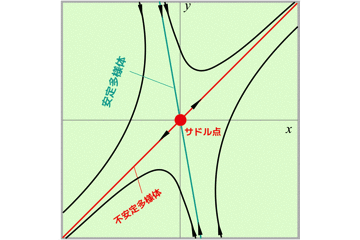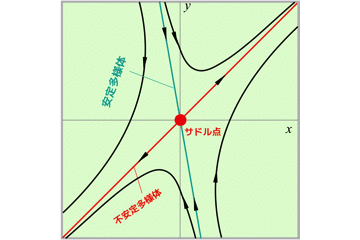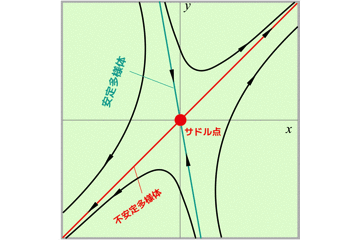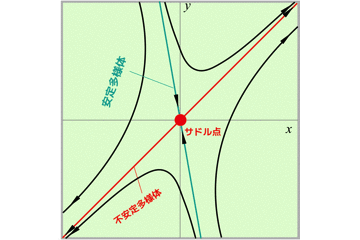
ベクトル場の流れを観察すると,流れと安定な固定点があるので解が求まります.
このアプローチによって,初期位置π/4だったものが,最終的にはπになることがわかると思います.
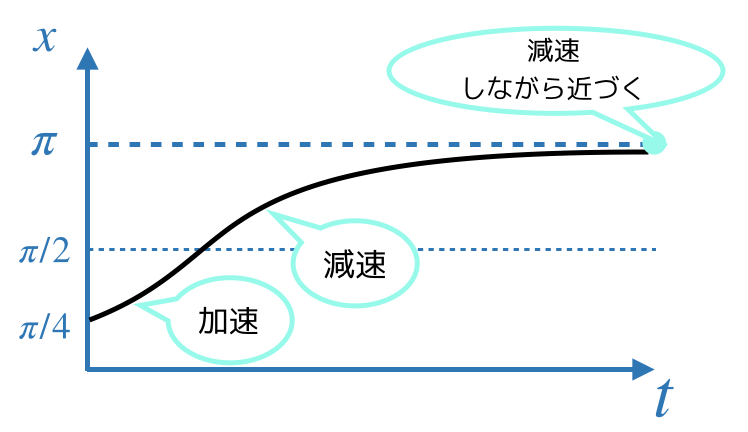
π/2を境に加速と減速を経て,最終的には,x=πへと落ち着きます.
このベクトル場を用いたアイデア,任意の一次元系に拡張することができるので是非是非いろんな式で試してみてください!
こちらの本をすごく参考にしました.かなりオススメの一冊です.