- 線形分離が可能な場合のSVMを理解できた人
- SVMの理論的な仕組みを理解したい人
- 機械学習に興味がある人
こんにちは.けんゆー(@kenyu0501_)です.
前回の記事では,線形分離可能な場合のサポートベクターマシンの説明を行いました.
ハードマージンというものですね.
この記事はこんな人におすすめです. サポートベクターマシンの理屈を詳しく理解したい人 機械学習の勉強をしている…
ハードマージンでは,訓練データを完全に分離するための境界を引く関数を決める制約がキツすぎるという点を問題としてあげてました.
そのため,この記事では,線形分離が不可能な場合のSVM(ソフトマージン)の基本的な仕組みの解説をしていきたいと思います.
解説動画をアップしました
線形分離不可能の場合とは
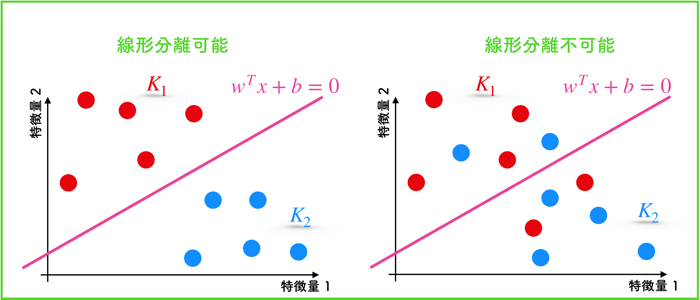
線形分離可能なデータと線形分離不可能なデータについて以下に示します.

直線でデータを2つのクラスに分離できるというのは,現実的に非常に稀な場合です.
直線のみで完全に分離ができるという仮定は,かなり珍しいのですね.

直線のみで完全に分けられるという制約はマジで厳しい場合もあるよ!
だいたいのデータ構造は線形分離不可能な場合が多いのです.
そのため,線形分離が不可能なデータを扱うための対処法を学ぶ必要があります.
ソフトマージン:スラッグ変数ξを導入して制約を弱める
直線で完全に分離できないデータに対しては,スラッグ変数ξを導入して制約を弱めるということを行います.
この拡張をソフトマージンといいます.
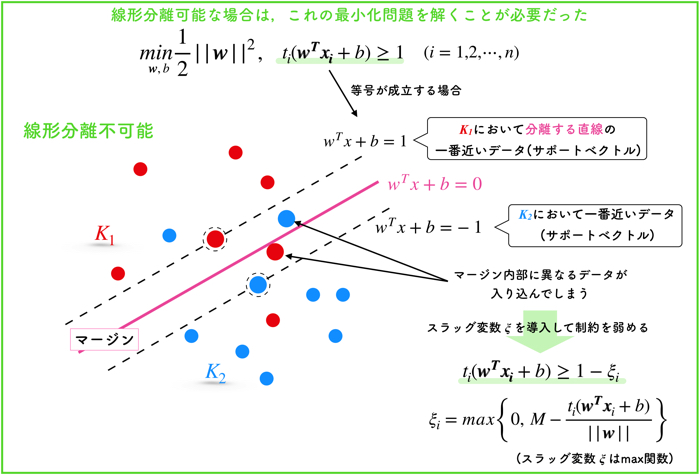
ここで,ξというのは,Max関数で,2つの値のうち,大きい方をとります.
つまり,0か,各データとマージンの差で,大きい方ですね.
少し具体的なデータ点を考えて,ξのイメージをしましょう.
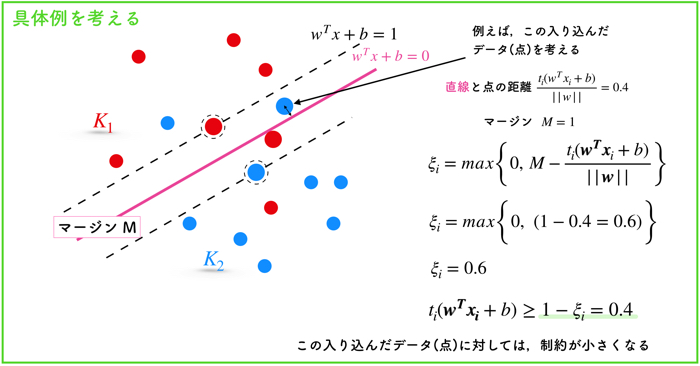
マージンの内側に入り込んだ1つのデータ(点)を考えます.
このとき,マージンと点との差は,0.6になります.
そのため,ξはMax関数なので,0.6になります.
このξの効果は,制約条件の1を0.6小さくするので,制約条件が0.4よりも大きければ良いということになり,弱まります.
こういった制約条件を弱めることをソフトマージンと呼ぶのでしたね.
(前回の線形分離可能なマージンをハードマージンでした.)
SVMの主問題:ソフトマージンの定式化
以上を踏まえて,今回の線形分離不可能な場合のマージンの定式化をします.
ハードマージンとソフトマージンの比較するような形の方が理解しやすいと思います.
(このような最適化問題をSVMの主問題と呼びます.)

ハードマージンは,線形分離可能な場合の定式化です.
ここでは,ソフトマージンに注目しましょう.
目的関数を小さくする最適化問題を解きますが,目的関数に,ξの総和の項が入っていることがわかります.
ここで,ξは正です.また制約条件を弱める意味がありました.
また,Cというのは,正則化係数と呼ばれる正の定数です.
このパラメータは,ハイパーパラメータと言って,SVMを使用する人が事前に定めるものです.
ξの総和をどれほど重要視するのか?ということを表したものです.
目的関数の最小化を図るには,2項のバランスを上手く取らないといけません.
目的関数の第1項と第2項の意味
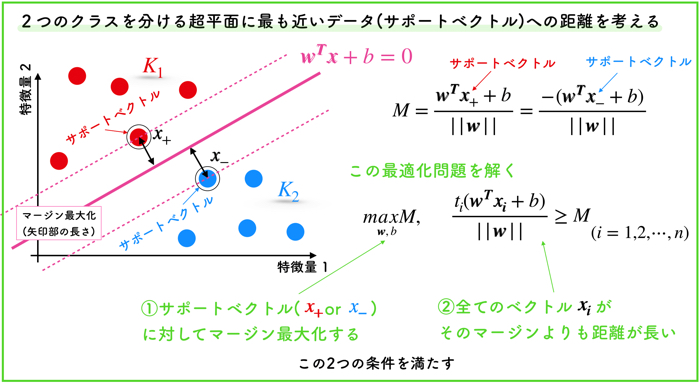
第1項は,マージン最大化の働きを持ちます.ハードマージンと同じですね.
第2項は,元の制約条件に対する違反の度合いであるξがなるべく小さくなるように制約しています.
この項によって,マージンが大きくても誤分類が多く発生するような分類器が作られにくくなります.
具体的に説明すると,マージンを大きくしようとすると,マージン内部に入り込むデータが増えます.
目的関数の第1項は減少する代わりに,第2項(ξの総和)が増加するということです.
また,ξの総和をほぼほぼ0にすると,間違ったデータの侵入を許さないので,マージンが物凄く狭い幅になります.
(マージンを大きく取れないことになります.)
そのため,2項のバランスを上手く取らなければいけません.

ハイパーパラメータを適切に定めよう!
正則化係数 C→∞ にしたらどうなるのか!?
正則化係数Cに関しては,ハイパーパラメータなので,使用者が事前に定めなくてはいけない定数です.
では,これが非常に大きい値をとるとどうなるのでしょうか?
答えは,「ハードマージンになる!」です.
C→∞では,ξ が要素を持った場合,目的関数も∞になるので,ξ が常に0でなければいけません.
そのため,Cがかなり大きな値になるソフトマージンに関しては,ハードマージンに一致するということが分かっています.
適切なパラメータCを定めるためには,データに依存するため,交差検証などを用いてCを評価しながら最もよい値を選択してくださいね!
多くのソフトウェアは主問題を解かずに双対問題を解く
これまでは,SVMの主問題を解きましたが,実際にSVMを計算する場合は,双対問題というものを解いて分類器を作成します.
SVMにおいては,主問題よりも式を変形して双対問題にした方が解きやすいのです.
また,分離境界の非線形化を考える上でも双対問題の方が便利です.
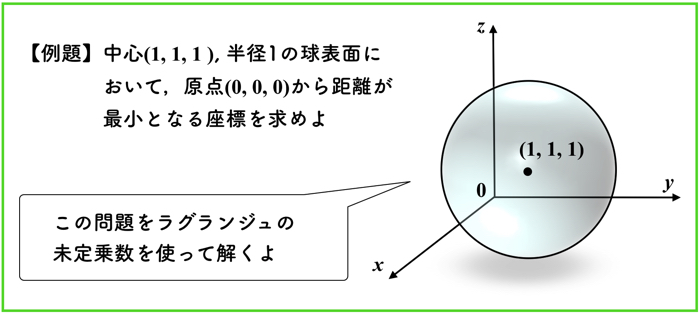
実際には,ラグランジュの未定乗数法などを用いて,式を変形します.
次回はその説明を行います.
この記事はこんな人にオススメです SVMを使えるだけではなく,きちんと理解したい人 SVMを解く最適化問題に使…


めちゃくちゃわかりやすいです。本を読んでもいまいちSVMの数式が腑に落ちませんでしたが、ようやく理解できました。本当にありがとうございます!
keisukeさん,
コメントありがとうございます.
そういって頂き,書き手冥利です.嬉しいです(^^)